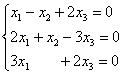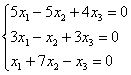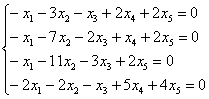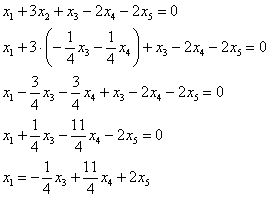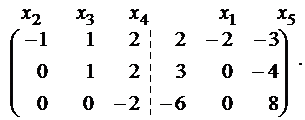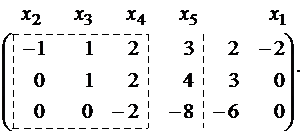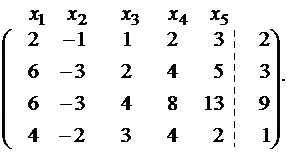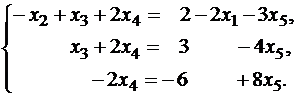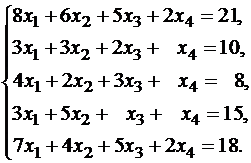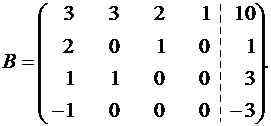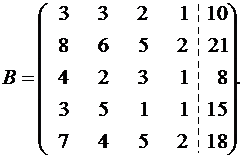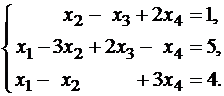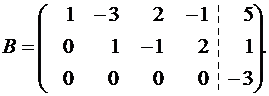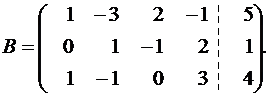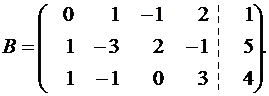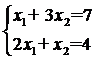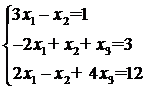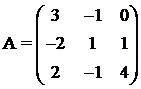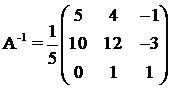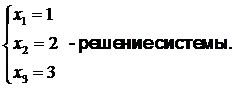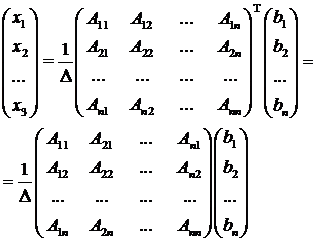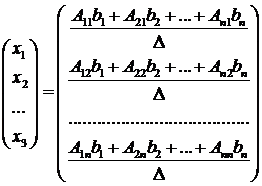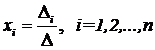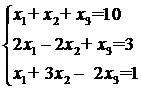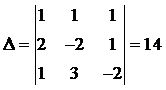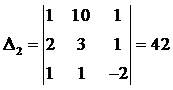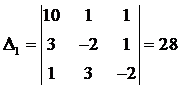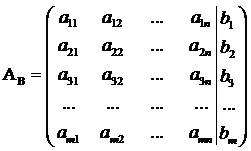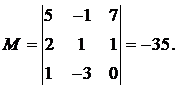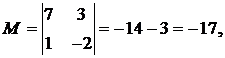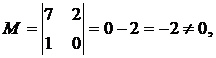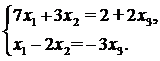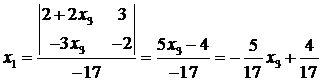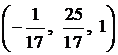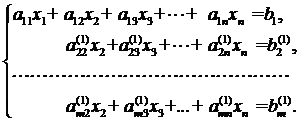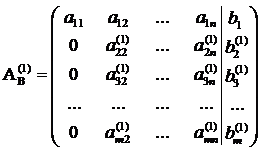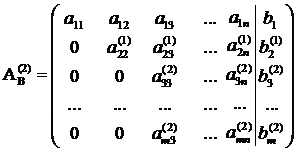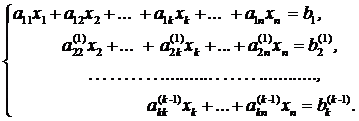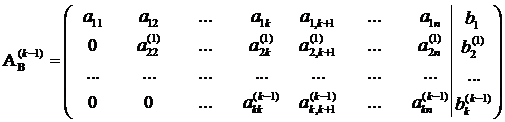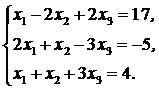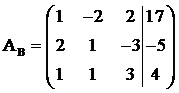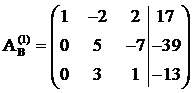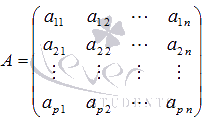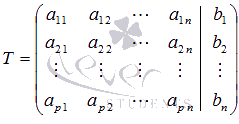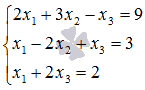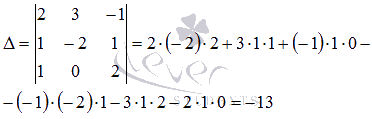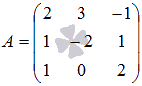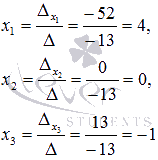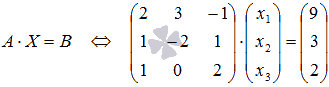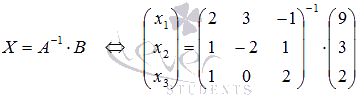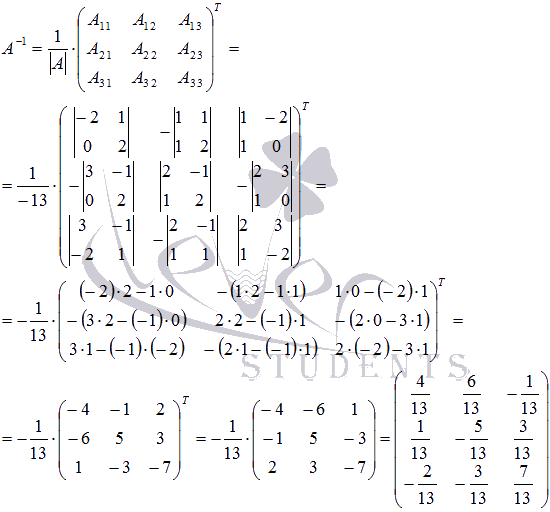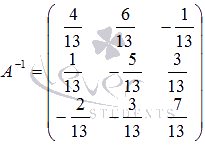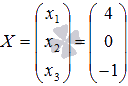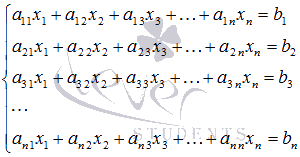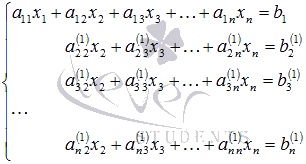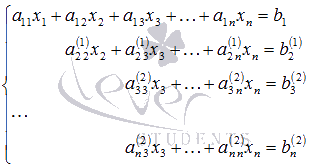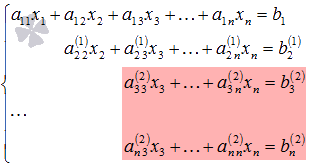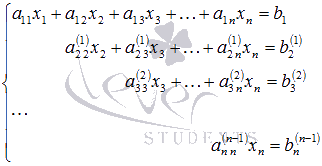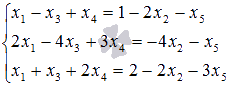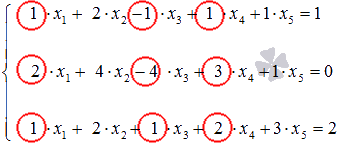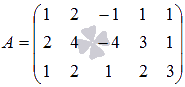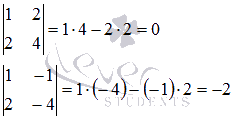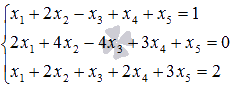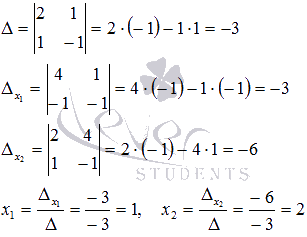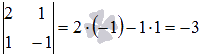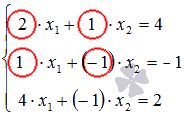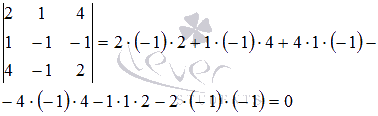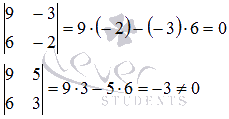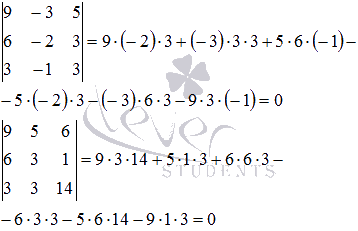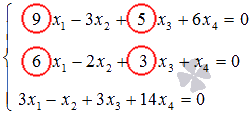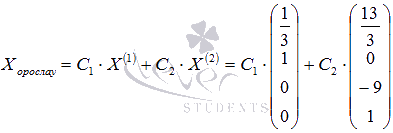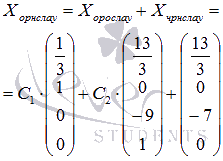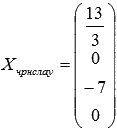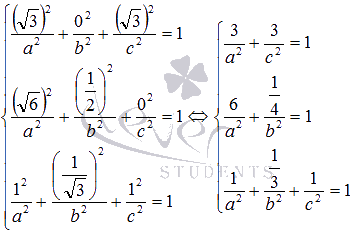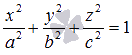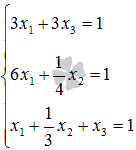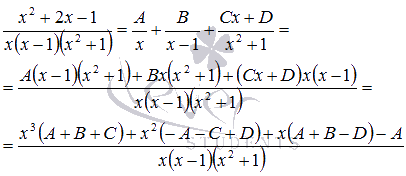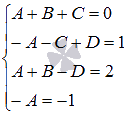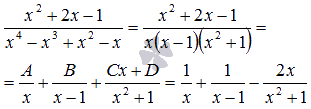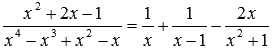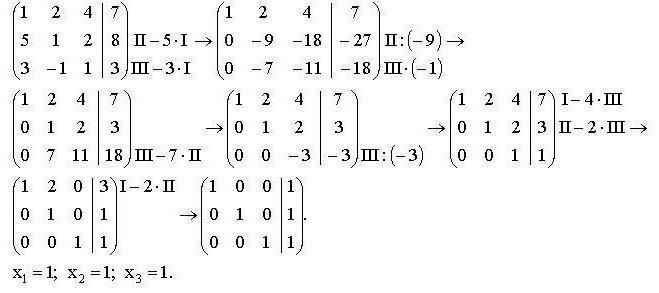Мы продолжим шлифовать технику
элементарных преобразованийна
однородной системе линейных уравнений.
По первым абзацам материал может показаться скучным и заурядным, однако
данное впечатление
обманчиво. Помимо дальнейшей отработки технических приёмов будет много новой информации, поэтому, пожалуйста, постарайтесь не пренебрегать примерами данной статьи.
Что такое однородная система линейных уравнений?
Ответ напрашивается сам собой. Система линейных уравнений является однородной, если свободный член
каждогоуравнения системы равен нулю. Например:
Совершенно ясно, что
однородная система всегда совместна, то есть всегда имеет решение. И, прежде всего, в глаза бросается так называемое
тривиальноерешение
. Тривиальное, для тех, кто совсем не понял смысл прилагательного, значит, беспонтовое. Не академично, конечно, но зато доходчиво =) …Чего ходить вокруг да около, давайте выясним, нет ли у данной системы каких-нибудь других решений:
Пример 1
Решение: чтобы решить однородную систему необходимо записать
матрицу системыи с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3.
(2) К третьей строке прибавили вторую строку, умноженную на –1.
Делить третью строку на 3 не имеет особого смысла.
В результате элементарных преобразований получена эквивалентная однородная система
, и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.
Ответ:
Сформулируем очевидный критерий: однородная система линейных уравнений имеет
только тривиальное решение, если
ранг матрицы системы(в
данном случае
3) равен количеству переменных (в данном случае – 3 шт.).
Разогреваемся и настраиваем свой радиоприёмник на волну элементарных преобразований:
Пример 2
Решить однородную систему линейных уравнений
Чтобы окончательно закрепить алгоритм, разберём финальное задание:
Пример 7
Решить однородную систему, ответ записать в векторной форме.
Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
(1) У первой строки сменили знак. Ещё раз заостряю внимание на неоднократно встречавшемся приёме, который позволяет существенно упростить следующее действие.
(1) Ко 2-й и 3-й строкам прибавили первую строку. К 4-й строке прибавили первую строку, умноженную на 2.
(3) Последние три строки пропорциональны, две из них удалили.
В результате получена стандартная ступенчатая матрица, и решение продолжается по накатанной колее:
– базисные переменные;
– свободные переменные.
Выразим базисные переменные через свободные переменные. Из 2-го уравнения:
– подставим в 1-е уравнение:
Таким образом, общее решение:
Поскольку в рассматриваемом примере три свободные переменные, то фундаментальная система содержит три вектора.
Подставим тройку значений
в общее решение и получим вектор , координаты которого удовлетворяют каждому уравнению однородной системы. И снова повторюсь, что крайне желательно проверять каждый полученный вектор – времени займет не так много, а от ошибок убережёт стопроцентно.
Для тройки значений
находим вектор
И, наконец, для тройки
получаем третий вектор:
Ответ: , где
Желающие избежать дробных значений могут рассмотреть тройки
и получить ответ в эквивалентном виде:
К слову о дробях. Посмотрим на полученную в задаче матрицу
и зададимся вопросом – нельзя ли упростить дальнейшее решение? Ведь здесь мы сначала выразили через дроби базисную переменную , потом через дроби базисную переменную , и, надо сказать, процесс это был не самый простой и не самый приятный.
Второй вариант решения:
Идея состоит в том, чтобы попытаться
выбрать другие базисные переменные. Посмотрим на матрицу и заметим две единицы в третьем столбце. Так почему бы не получить ноль вверху? Проведём ещё одно элементарное преобразование:
Пример 1
. Найти общее решение и какое–нибудь частное решение системы
Решениевыполняем с помощью калькулятора . Выпишем расширенную и основную матрицы:
Пунктиром отделена основная матрица A. Сверху пишем неизвестные системы, имея в виду возможную перестановку слагаемых в уравнениях системы. Определяя ранг расширенной матрицы, одновременно найдем ранг и основной. В матрице B первый и второй столбцы пропорциональны. Из двух пропорциональных столбцов в базисный минор может попасть только один, поэтому перенесем, например, первый столбец за пунктирную черту с обратным знаком. Для системы это означает перенос членов с x 1 в правую часть уравнений.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы. Работаем с первой строкой: умножим первую строку матрицы на (-3) и прибавим ко второй и третьей строкам по очереди. Затем первую строку умножим на (-2) и прибавим к четвертой.
Вторая и третья строки пропорциональны, следовательно, одну из них, например вторую, можно вычеркнуть. Это равносильно вычеркиванию второго уравнения системы, так как оно является следствием третьего.
Теперь работаем со второй строкой: умножим ее на (-1) и прибавим к третьей.
Минор, обведенный пунктиром, имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на главной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rangA = rangB = 3 .
Минор
является базисным. В него вошли коэффициенты при неизвестных x 2 , x 3 , x 4 , значит, неизвестные x 2 , x 3 , x 4 – зависимые, а x 1 , x 5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор (что соответствует пункту 4 приведенного выше алгоритма решения).
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид
Методом исключения неизвестных находим:
x 4 =3-4x 5 , x 3 =3-4x 5 -2x 4 =3-4x 5 -6+8x 5 =-3+4x 5
x 2 =x 3 +2x 4 -2+2x 1 +3x 5 = -3+4x 5 +6-8x 5 -2+2x 1 +3x 5 = 1+2x 1 -x 5
Получили соотношения, выражающие зависимые переменные x 2 , x 3 , x 4 через свободные x 1 и x 5 , то есть нашли общее решение:

Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Найдем два частных решения:
1) пусть x 1 = x 5 = 0, тогда x 2 = 1, x 3 = -3, x 4 = 3;
2) положим x 1 = 1, x 5 = -1, тогда x 2 = 4, x 3 = -7, x 4 = 7.
Таким образом, нашли два решения: (0,1,-3,3,0) – одно решение, (1,4,-7,7,-1) – другое решение.
Пример 2. Исследовать совместность, найти общее и одно частное решение системы
Решение. Переставим первое и второе уравнения, чтобы иметь единицу в первом уравнении и запишем матрицу B.
Получим нули в четвертом столбце, оперируя первой строкой:
Теперь получим нули в третьем столбце с помощью второй строки:
Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третью строку умножим на (–2) и прибавим к четвертой:
Видим, что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
-x 1 =-3 → x 1 =3; x 2 =3-x 1 → x 2 =0; x 3 =1-2x 1 → x 3 =5.
x 4 = 10- 3x 1 – 3x 2 – 2x 3 = 11.
Пример 3. Исследовать систему на совместность и найти решение, если оно существует.
Решение. Составляем расширенную матрицу системы.
Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Умножая первую строку на (-1), складываем ее с третьей:
Умножим вторую строку на (-2) и прибавим к третьей:
Система несовместна, так как в основной матрице получили строку, состоящую из нулей, которая вычеркивается при нахождении ранга, а в расширенной матрице последняя строка останется, то есть r B > r A .
Задание. Исследовать данную систему уравнений на совместность и решить ее средствами матричного исчисления .
Решение
Пример. Доказать совместимость системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса ; 2) методом Крамера . (ответ ввести в виде: x1,x2,x3)
Решение :doc :doc :xls
Ответ:2,-1,3.
Пример. Дана система линейных уравнений. Доказать ее совместность. Найти общее решение системы и одно частное решение.
Решение
Ответ:x 3 = — 1 + x 4 + x 5 ; x 2 = 1 — x 4 ; x 1 = 2 + x 4 — 3x 5
Задание. Найти общее и частное решения каждой системы.
Решение.Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-3). Добавим 3-ую строку к 2-ой:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то
система является совместной
.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x 1 ,x 2 ,x 3 , значит, неизвестные x 1 ,x 2 ,x 3 – зависимые (базисные), а x 4 ,x 5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
27x 3 =
— x 2 + 13x 3 = — 1 + 3x 4 — 6x 5
2x 1 + 3x 2 — 3x 3 = 1 — 3x 4 + 2x 5
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x 1 ,x 2 ,x 3 через свободные x 4 ,x 5 , то есть нашли
общее решение
:
x 3 = 0
x 2 = 1 — 3x 4 + 6x 5
x 1 = — 1 + 3x 4 — 8x 5
неопределенной
, т.к. имеет более одного решения.
Задание. Решить систему уравнений.
Ответ😡 2 = 2 — 1.67x 3 + 0.67x 4
x 1 = 5 — 3.67x 3 + 0.67x 4
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является
неопределенной
Системы линейных алгебраических уравнений
1. Системы линейных алгебраических уравнений
Системой линейных
алгебраических уравнений (СЛАУ) называется система вида
(4.1)
Решением системы
(4.1) называется такая совокупность
nчисел
При подстановке которых каждое уравнение системы обращается
в верное равенство.
Решить систему означает найти все ее решения или доказать, что ни одного
решения нет.
СЛАУ называется совместной, если она имеет хотя бы одно решение, и несовместной,
если она решений не имеет.
Если совместная система имеет только одно решение, то она называется
определенной, и неопределенной, если она имеет более чем одно решение.
Например, система уравнений
совместная и определенная, так как имеет единственное решение
; система
несовместная, а система
совместная и неопределенная, так как имеет
более одного решения
.
Две системы уравнений называются равносильными или эквивалентными, если они
имеют одно и то же множество решений. В частности, две несовместные системы
считаются эквивалентными.
Основной матрицей СЛАУ (4.1) называется матрица А размера
, элементами которой являются коэффициенты
при неизвестных данной системы, то есть
.
Матрицей неизвестных СЛАУ (4.1) называется матрица-столбец Х, элементами
которой являются неизвестные системы (4.1):
Матрицей свободных членов СЛАУ (4.1) называется матрица-столбец В,
элементами которой являются свободные члены данной СЛАУ:
С учетом введенных
понятий СЛАУ (4.1) можно записать в матричном виде или
.(4.2)
2. Решение систем линейных
уравнений. Метод обратной матрицы
Перейдем к изучению
СЛАУ (4.1), которой соответствует матричное уравнение (4.2). Сначала рассмотрим
частный случай, когда число неизвестных равно числу уравнений данной системы () и , то есть основная матрица системы невырождена. В этом случае, согласно предыдущему
пункту, для матрицы существует
единственная
обратная матрица
. Ясно,
что она согласована с матрицами и . Покажем это. Для этого умножим слева обе части матричного
уравнения (4.2) на матрицу :
Следовательно, с учетом свойств умножения
матриц получаем
Так как , а , тогда
.(4.3)
Убедимся, что найденное значение является решением
исходной системы. Подставив (4.3) в уравнение (4.2), получим
, откуда имеем .
Покажем, что это
решение единственное. Пусть матричное уравнение (4.2) имеет другое решение , которое удовлетворяет равенству
Покажем, что матрица
равна матрице
С этой целью умножим
предыдущее равенство слева на матрицу .
В результате получим
Такое решение
системы уравнений с неизвестными
называется решением системы (4.1) методом обратной матрицы.
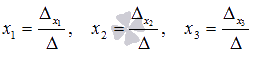
Пример. Найти решение системы
.
Выпишем матрицу системы:
,
Для этой матрицы ранее (занятие 1) мы уже
нашли обратную:
или
Здесь мы вынесли
общий множитель , так как нам в дальнейшем нужно будет произведение .
Ищем решение по
формуле: .
3. Правило и формулы Крамера
Рассмотрим систему линейных уравнений с неизвестными
От матричной формы
(4.3) перейдем к более удобным и в ряде случаев более простым при решении
прикладных задач формулам для нахождения решений системы линейных
алгебраических уравнений.
Учитывая равенство , или в
развернутом виде
.
Таким образом, после перемножения матриц
получаем:
или
.
Заметим, что сумма есть разложение
определителя
по элементам первого столбца, который
получается из определителя путем замены первого
столбца коэффициентов столбцом из свободных членов.
Таким образом, можно
сделать вывод, что
Аналогично: , где получен из путем замены второго
столбца коэффициентов столбцом из свободных членов,
.
Следовательно, нами найдено решение заданной
системы по равенствам
, , ,
известным и как формулы Крамера.
Для нахождения
решения СЛАУ, последние равенства можно записать в общем виде следующим
образом:
.(4.4)
Согласно этим формулам, имеем правило
Крамера для решения СЛАУ:
—
по матрице системы вычисляется определитель системы ;
—
если , то в матрице системы каждый столбец последовательно заменяется
столбцом свободных членов и вычисляются определители
получаемых при этом
матриц;
—
решение системы находится по формулам Крамера (4.4).
Пример. С помощью формул Крамера решить
систему уравнений
Решение. Определитель данной системы
.
Так как , то формулы Крамера имеют смысл, то есть система имеет единственное
решение. Находим определители:
,
,
.
Следовательно, по формулам (4.4) получаем:
,
,
.
Найденные значения
переменных подставляем в уравнения системы и убеждаемся, что они являются ее
решением.
Упражнение. Проверку этого факта сделайте
самостоятельно.
Критерий совместности СЛАУ (теорема Кронекера-Капелли)
Расширенной матрицей
системы (4.1)
называется матрица, получаемая добавлением к основной матрице А справа столбца
свободных членов с отделением его вертикальной чертой, то есть матрица
.
Заметим, что при
появлении у матрицы новых столбцов ранг может увеличиться, следовательно
. Расширенная матрица играет очень важную роль в вопросе совместности
(разрешимости) системы уравнений. Исчерпывающий ответ на этот вопрос дает
теорема Кронекера-Капелли.
Сформулируем
теорему Кронекера-Капелли(без
доказательства).
Система линейных
алгебраических уравнений (4.1) совместна тогда и только тогда, когда ранг
матрицы системы равен рангу расширенной матрицы
. Если
– число неизвестных
системы, то система имеет единственное решение, а если
, то система имеет бесчисленное множество решений.
Опираясь на теорему
Кронекера-Капелли, сформулируем алгоритм решения произвольной системы линейных
уравнений:
1.
Вычисляют ранги
основной и расширенной матриц СЛАУ. Если
, то система не имеет решений (несовместна).
2.
Если
, система совместна. В этом случае берут любой отличный от
нуля минор основной матрицы порядка и рассматривают уравнений, коэффициенты которых входят в этот базисный минор,
а остальные уравнения отбрасывают. Неизвестные коэффициенты, которые входят в
этот базисный минор, объявляют главными или базисными, а остальные свободными
(неосновными). Новую систему переписывают, оставляя в левых частях уравнений
только члены, содержащие базисных неизвестных, а все остальные члены уравнений, содержащих
неизвестных, переносят
в правые части уравнений.
3.
Находят выражения
базисных неизвестных через свободные. Полученные решения новой системы с базисными неизвестными называются
общим решением
СЛАУ (4.1).
4.
Придавая свободным
неизвестным некоторые
числовые значения
, находят так называемые частные
решения.
Проиллюстрируем
применение теоремы Кронекера-Капелли и вышеприведенного алгоритма на конкретных
примерах.
Пример. Определить совместность системы
уравнений
Решение. Запишем матрицу системы и определим
ее ранг.
Имеем:
Так как матрица имеет порядок , то наивысший порядок миноров равен 3. Число различных
миноров третьего порядка Нетрудно убедиться,
что все они равны нулю (проверьте самостоятельно). Значит, . Ранг основной матрицы равен двум, так как существует
отличный от нуля минор второго порядка этой матрицы, например,
Ранг расширенной
матрицы этой
системы равен трем, так как существует отличный минор третьего порядка этой
матрицы, например,
Таким образом,
согласно критерию Кронекера-Капелли, система несовместна, то есть не имеет
решений.
Пример. Исследовать совместность системы
уравнений
Решение. Ранг основной матрицы этой системы равен
двум, так как, например, минор второго порядка равен
а все миноры третьего порядка основной
матрицы равны нулю. Ранг расширенной матрицы также равен двум,
например,
а все миноры третьего порядка расширенной
матрицы равны нулю (убедиться самостоятельно). Следовательно, система
совместна.
Возьмем за базисный
минор, например . В этот базисный минор не входят элементы третьего
уравнения, поэтому ее отбрасываем.
Неизвестные и объявляем базисными,
так как их коэффициенты входят в базисный минор, неизвестную объявляем свободной.
В первых двух
уравнениях члены, содержащие переменную , перенесем в правые части. Тогда получим систему
Решаем эту систему с
помощью формул Крамера.
,
.
Таким образом, общим решением исходной
системы является бесконечное множество наборов вида
,
где – любое действительное
число.
Частным решением данного уравнения будет,
например, набор
, получающийся при .
4.
Решение систем линейных алгебраических уравнений методом Гаусса
Одним из наиболее
эффективных и универсальных методов решений СЛАУ является метод Гаусса. Метод
Гаусса состоит из однотипных циклов, позволяющихпоследовательно исключать неизвестные СЛАУ. Первый
цикл направлен на то, чтобы во всех уравнениях, начиная со второго, обнулить
все коэффициенты при
. Опишем первый цикл. Полагая, что в системе коэффициент
(если это не так, то следует на первое место
поставить уравнение с отличным от нуля коэффициентом при
x1 и переобозначить коэффициенты), преобразуем систему
(4.1) следующим образом: первое уравнение оставляем без изменения, а из всех
остальных уравнений исключаем неизвестную
x1
с помощью элементарных преобразований. Для этого умножим обе части первого
уравнения на
и сложим почленно со вторым
уравнением системы. Затем умножим обе части первого уравнения на
и сложим с третьим уравнением
системы. Продолжая этот процесс, на последнем шаге цикла умножим обе части
первого уравнения на
и
сложим с последним уравнением системы. Первый цикл завершен, в результате
получим эквивалентную систему
(4.5)
Замечание.Для удобства записи обычно используют расширенную матрицу системы. После
первого цикла данная матрица принимает следующий вид:
(4.6)
Второй цикл является повторением первого цикла. Предположим, что коэффициент
. Если это не так, то перестановкой уравнений местами добьемся того, что
. Первое и второе уравнение системы (4.5) перепишем в
новую систему
(в
дальнейшем будем оперировать только расширенной матрицей).
Умножим второе уравнение (4.5) или вторую строку матрицы (4.6) на
, сложим с третьим уравнением системы (4.5) или третьей строкой матрицы
(4.6). Аналогично поступаем с остальными уравнениями системы. В результате получим
эквивалентную систему:
(4.7)
Продолжая процесс
последовательного исключения неизвестных, после
шага, получим расширенную матрицу
(4.8)
Последние
уравнений для совместной системы
(4.1) являются тождествами
. Если хотя бы одно из чисел
не
равно нулю, то соответствующее равенство противоречиво, следовательно, система
(4.1) несовместна. В совместной системе при ее решении последние
уравнений можно не рассматривать.
Тогда полученная эквивалентная система (4.9) и соответствующая расширенная
матрица (4.10) имеют вид
(4.9)
(4.10)
После отбрасывания уравнений, являющихся тождествами, число оставшихся
уравнений может быть либо равно числу переменных
, либо быть меньше числа переменных. В
первом случае матрица имеет треугольный вид, а во втором – ступенчатый. Переход
от системы (4.1) к равносильной ей системе (4.9) называется прямым ходом метода
Гаусса, а нахождение неизвестных из системы (4.9) – обратным ходом.
Пример. Решить систему методом Гаусса:
.
Решение. Расширенная
матрица этой системы имеет вид
.
Проведем следующие преобразования расширенной матрицы системы: умножим
первую строку на
и сложим
со второй строкой, а также умножим первую строку на
и сложим с третьей строкой. Результатом
будет расширенная матрица первого цикла (в дальнейшем все преобразования будем
изображать в виде схемы)
.
|
|

Решение систем линейных алгебраических уравнений (СЛАУ), несомненно, является важнейшей темой курса линейной алгебры. Огромное количество задач из всех разделов математики сводится к решению систем линейных уравнений. Этими факторами объясняется причина создания данной статьи. Материал статьи подобран и структурирован так, что с его помощью Вы сможете
- подобрать оптимальный метод решения Вашей системы линейных алгебраических уравнений,
- изучить теорию выбранного метода,
- решить Вашу систему линейных уравнений, рассмотрев подробно разобранные решения характерных примеров и задач.
Краткое описание материала статьи.
Сначала дадим все
необходимые определения
, понятия и введем обозначения.
Далее рассмотрим методы решения систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных переменных и которые имеют единственное решение. Во-первых, остановимся на методе Крамера, во-вторых, покажем матричный метод решения таких систем уравнений, в-третьих, разберем метод Гаусса (метод последовательного исключения неизвестных переменных). Для закрепления теории обязательно решим несколько СЛАУ различными способами.
После этого перейдем к решению систем линейных алгебраических уравнений
общего вида
, в которых число уравнений не совпадает с числом неизвестных переменных или основная матрица системы является вырожденной. Сформулируем теорему Кронекера — Капелли, которая позволяет установить совместность СЛАУ. Разберем решение систем (в случае их совместности) с помощью понятия базисного минора матрицы. Также рассмотрим метод Гаусса и подробно опишем решения примеров.
Обязательно остановимся на структуре общего решения однородных и неоднородных систем линейных алгебраических уравнений. Дадим понятие фундаментальной системы решений и покажем, как записывается общее решение СЛАУ с помощью векторов фундаментальной системы решений. Для лучшего понимания разберем несколько примеров.
В заключении рассмотрим системы уравнений, сводящиеся к линейным, а также различные задачи, при решении которых возникают СЛАУ.
Навигация по странице.
Определения, понятия, обозначения.
Будем рассматривать системы из p
линейных алгебраических уравнений с n
неизвестными переменными (p
может быть равно n
) вида
Неизвестные переменные, — коэффициенты (некоторые действительные или комплексные числа), — свободные члены (также действительные или комплексные числа).
Такую форму записи СЛАУ называют
координатной.
В
матричной формезаписи эта система уравнений имеет вид ,
где
— основная матрица системы, — матрица-столбец неизвестных переменных, — матрица-столбец свободных членов.
Если к матрице А
добавить в качестве (n+1)-ого
столбца матрицу-столбец свободных членов, то получим так называемую
расширенную матрицусистемы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т
, а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,
Решением системы линейных алгебраических уравненийназывают набор значений неизвестных переменных , обращающий все уравнения системы в тождества. Матричное уравнение при данных значениях неизвестных переменных также обращается в тождество .
Если система уравнений имеет хотя бы одно решение, то она называется
совместной.
Если система уравнений решений не имеет, то она называется
несовместной.
Если СЛАУ имеет единственное решение, то ее называют
определенной; если решений больше одного, то –
неопределенной.
Если свободные члены всех уравнений системы равны нулю
, то система называется
однородной, в противном случае –
неоднородной.
Мнение эксперта:
Система линейных алгебраических уравнений является важным инструментом в математике и ее приложениях. Эксперты отмечают, что решение таких систем имеет широкое применение в физике, экономике, инженерии и других областях. Они подчеркивают, что понимание и умение работать с системами линейных уравнений является ключевым навыком для специалистов в различных областях науки и техники. Эксперты также отмечают, что методы решения систем линейных уравнений постоянно развиваются, что открывает новые возможности для применения этого математического инструмента в различных областях.

Решение элементарных систем линейных алгебраических уравнений.
Если число уравнений системы равно числу неизвестных переменных и определитель ее основной матрицы не равен нулю, то такие СЛАУ будем называть
элементарными. Такие системы уравнений имеют единственное решение, причем в случае однородной системы все неизвестные переменные равны нулю.
Такие СЛАУ мы начинали изучать в средней школе. При их решении мы брали какое-нибудь одно уравнение, выражали одну неизвестную переменную через другие и подставляли ее в оставшиеся уравнения, следом брали следующее уравнение, выражали следующую неизвестную переменную и подставляли в другие уравнения и так далее. Или пользовались методом сложения, то есть, складывали два или более уравнений, чтобы исключить некоторые неизвестные переменные. Не будем подробно останавливаться на этих методах, так как они по сути являются модификациями метода Гаусса.
Основными методами решения элементарных систем линейных уравнений являются метод Крамера, матричный метод и метод Гаусса. Разберем их.
Решение систем линейных уравнений методом Крамера.
Пусть нам требуется решить систему линейных алгебраических уравнений
в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, .
Пусть — определитель основной матрицы системы, а
— определители матриц, которые получаются из А
заменой
1-ого, 2-ого, …, n-ого
столбца соответственно на столбец свободных членов:
При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как
. Так находится решение системы линейных алгебраических уравнений методом Крамера.
Пример.
Методом Крамера
.
Решение.
Основная матрица системы имеет вид
. Вычислим ее определитель (при необходимости смотрите статью ):
Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.
Составим и вычислим необходимые определители
(определитель получаем, заменив в матрице А
первый столбец на столбец свободных членов , определитель — заменив второй столбец на столбец свободных членов, — заменив третий столбец матрицы А
на столбец свободных членов):
Находим неизвестные переменные по формулам
:
Ответ:
Основным недостатком метода Крамера (если это можно назвать недостатком) является трудоемкость вычисления определителей, когда число уравнений системы больше трех.
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть система линейных алгебраических уравнений задана в матричной форме , где матрица A
имеет размерность n
на n
и ее определитель отличен от нуля.
Так как , то матрица А
– обратима, то есть, существует обратная матрица . Если умножить обе части равенства на слева, то получим формулу для нахождения матрицы-столбца неизвестных переменных . Так мы получили решение системы линейных алгебраических уравнений
матричным методом
.
Пример.
Решите систему линейных уравнений
матричным методом.
Решение.
Перепишем систему уравнений в матричной форме:
Так как
то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как
.
Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицы А
(при необходимости смотрите статью ):
Осталось вычислить — матрицу неизвестных переменных, умножив обратную матрицу
на матрицу-столбец свободных членов (при необходимости смотрите статью ):
Ответ:
или в другой записи x 1 = 4, x 2 = 0, x 3 = -1
.
Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.
Решение систем линейных уравнений методом Гаусса.
Пусть нам требуется найти решение системы из n
линейных уравнений с n
неизвестными переменными
определитель основной матрицы которой отличен от нуля.
Суть метода Гауссасостоит в последовательном исключении неизвестных переменных: сначала исключается x 1
из всех уравнений системы, начиная со второго, далее исключается x 2
из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная x n
. Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется
прямым ходом метода Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находится x n
, с помощью этого значения из предпоследнего уравнения вычисляется x n-1
, и так далее, из первого уравнения находится x 1
. Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется
обратным ходом метода Гаусса.
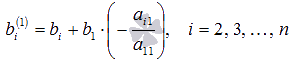
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x 1
из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому
уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид
где , а
.
К такому же результату мы бы пришли, если бы выразили x 1
через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x 1
исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому
уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид
где , а
. Таким образом, переменная x 2
исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x 3
, при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем x n
из последнего уравнения как , с помощью полученного значения x n
находим x n-1
из предпоследнего уравнения, и так далее, находим x 1
из первого уравнения.
Пример.
Решите систему линейных уравнений
методом Гаусса.
Решение.
Исключим неизвестную переменную x 1
из второго и третьего уравнения системы. Для этого к обеим частям второго и третьего уравнений прибавим соответствующие части первого уравнения, умноженные на и на соответственно:
Теперь из третьего уравнения исключим x 2
, прибавив к его левой и правой частям левую и правую части второго уравнения, умноженные на :
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x 3
:
Из второго уравнения получаем .
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .
Ответ:
X 1 = 4, x 2 = 0, x 3 = -1
.
Интересные факты
-
Метод Гауссаявляется одним из самых известных и широко используемых методов решения систем линейных алгебраических уравнений. Он был разработан немецким математиком Карлом Фридрихом Гауссом в 1810 году. Метод Гаусса основан на последовательном исключении переменных из системы уравнений, что приводит к треугольной системе уравнений, которую легко решить.
-
Правило Крамераявляется еще одним известным методом решения систем линейных алгебраических уравнений. Он был разработан швейцарским математиком Габриэлем Крамером в 1750 году. Правило Крамера основано на использовании определителей для решения системы уравнений. Определитель является числом, которое связано с системой уравнений и которое может быть использовано для определения решения системы.
-
Теорема Рунгеутверждает, что если система линейных алгебраических уравнений имеет единственное решение, то это решение непрерывно зависит от коэффициентов системы уравнений. Это означает, что если коэффициенты системы уравнений изменяются непрерывно, то решение системы уравнений также изменяется непрерывно. Теорема Рунге была доказана немецким математиком Карлом Рунге в 1894 году.
Решение систем линейных алгебраических уравнений общего вида.
В общем случае число уравнений системы p
не совпадает с числом неизвестных переменных n
:
Такие СЛАУ могут не иметь решений, иметь единственное решение или иметь бесконечно много решений. Это утверждение относится также к системам уравнений, основная матрица которых квадратная и вырожденная.
Теорема Кронекера – Капелли.
Прежде чем находить решение системы линейных уравнений необходимо установить ее совместность. Ответ на вопрос когда СЛАУ совместна, а когда несовместна, дает
теорема Кронекера – Капелли:
для того, чтобы система из p
уравнений с n
неизвестными (p
может быть равно n
) была совместна необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы, то есть, Rank(A)=Rank(T)
.
Рассмотрим на примере применение теоремы Кронекера – Капелли для определения совместности системы линейных уравнений.
Пример.
Выясните, имеет ли система линейных уравнений
решения.
Решение.
. Воспользуемся методом окаймляющих миноров. Минор второго порядка
отличен от нуля. Переберем окаймляющие его миноры третьего порядка:
Так как все окаймляющие миноры третьего порядка равны нулю, то ранг основной матрицы равен двум.
В свою очередь ранг расширенной матрицы
равен трем, так как минор третьего порядка
отличен от нуля.
Таким образом,
Rang(A) , следовательно, по теореме Кронекера – Капелли можно сделать вывод, что исходная система линейных уравнений несовместна.
Ответ:
Система решений не имеет.
Итак, мы научились устанавливать несовместность системы с помощью теоремы Кронекера – Капелли.
А как же находить решение СЛАУ, если установлена ее совместность?
Для этого нам потребуется понятие базисного минора матрицы и теорема о ранге матрицы.
Минор наивысшего порядка матрицы А
, отличный от нуля, называется
базисным.
Из определения базисного минора следует, что его порядок равен рангу матрицы. Для ненулевой матрицы А
базисных миноров может быть несколько, один базисный минор есть всегда.
Для примера рассмотрим матрицу
.
Все миноры третьего порядка этой матрицы равны нулю, так как элементы третьей строки этой матрицы представляют собой сумму соответствующих элементов первой и второй строк.
Базисными являются следующие миноры второго порядка, так как они отличны от нуля
Миноры
базисными не являются, так как равны нулю.
Теорема о ранге матрицы.
Если ранг матрицы порядка p
на n
равен r
, то все элементы строк (и столбцов) матрицы, не образующие выбранный базисный минор, линейно выражаются через соответствующие элементы строк (и столбцов), образующих базисный минор.
Что нам дает теорема о ранге матрицы?
Если по теореме Кронекера – Капелли мы установили совместность системы, то выбираем любой базисный минор основной матрицы системы (его порядок равен r
), и исключаем из системы все уравнения, которые не образуют выбранный базисный минор. Полученная таким образом СЛАУ будет эквивалентна исходной, так как отброшенные уравнения все равно излишни (они согласно теореме о ранге матрицы являются линейной комбинацией оставшихся уравнений).
В итоге, после отбрасывания излишних уравнений системы, возможны два случая.
Если число уравнений r
в полученной системе будет равно числу неизвестных переменных, то она будет определенной и единственное решение можно будет найти методом Крамера, матричным методом или методом Гаусса.
Пример.
.
Решение.
Ранг основной матрицы системы
равен двум, так как минор второго порядка
отличен от нуля. Ранг расширенной матрицы
также равен двум, так как единственный минор третьего порядка равен нулю
а рассмотренный выше минор второго порядка отличен от нуля. На основании теоремы Кронекера – Капелли можно утверждать совместность исходной системы линейных уравнений, так как Rank(A)=Rank(T)=2
.
В качестве базисного минора возьмем
. Его образуют коэффициенты первого и второго уравнений:
Третье уравнение системы не участвует в образовании базисного минора, поэтому исключим его из системы на основании теоремы о ранге матрицы:
Так мы получили элементарную систему линейных алгебраических уравнений. Решим ее методом Крамера:
Ответ:
x 1 = 1, x 2 = 2
.
Если число уравнений r
в полученной СЛАУ меньше числа неизвестных переменных n
, то в левых частях уравнений оставляем слагаемые, образующие базисный минор, остальные слагаемые переносим в правые части уравнений системы с противоположным знаком.
Неизвестные переменные (их r
штук), оставшиеся в левых частях уравнений, называются
основными.
Неизвестные переменные (их n — r
штук), которые оказались в правых частях, называются
свободными.
Теперь считаем, что свободные неизвестные переменные могут принимать произвольные значения, при этом r
основных неизвестных переменных будут выражаться через свободные неизвестные переменные единственным образом. Их выражение можно найти решая полученную СЛАУ методом Крамера, матричным методом или методом Гаусса.
Разберем на примере.
Пример.
Решите систему линейных алгебраических уравнений
.
Решение.
Найдем ранг основной матрицы системы
методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмем a 1 1 = 1
. Начнем поиск ненулевого минора второго порядка, окаймляющего данный минор:
Так мы нашли ненулевой минор второго порядка. Начнем поиск ненулевого окаймляющего минора третьего порядка:
Таким образом, ранг основной матрицы равен трем. Ранг расширенной матрицы также равен трем, то есть, система совместна.
Найденный ненулевой минор третьего порядка возьмем в качестве базисного.
Для наглядности покажем элементы, образующие базисный минор:
Оставляем в левой части уравнений системы слагаемые, участвующие в базисном миноре, остальные переносим с
противоположными знаками
в правые части:
Придадим свободным неизвестным переменным x 2
и x 5
произвольные значения, то есть, примем
, где — произвольные числа. При этом СЛАУ примет вид
Полученную элементарную систему линейных алгебраических уравнений решим методом Крамера:
Следовательно, .
В ответе не забываем указать свободные неизвестные переменные.
Ответ:
Где — произвольные числа.
Подведем итог.
Чтобы решить систему линейных алгебраических уравнений общего вида, сначала выясняем ее совместность, используя теорему Кронекера – Капелли. Если ранг основной матрицы не равен рангу расширенной матрицы, то делаем вывод о несовместности системы.
Если ранг основной матрицы равен рангу расширенной матрицы, то выбираем базисный минор и отбрасываем уравнения системы, которые не участвуют в образовании выбранного базисного минора.
Если порядок базисного минора равен числу неизвестных переменных, то СЛАУ имеет единственное решение, которое находим любым известным нам методом.
Если порядок базисного минора меньше числа неизвестных переменных, то в левой части уравнений системы оставляем слагаемые с основными неизвестными переменными, остальные слагаемые переносим в правые части и придаем свободным неизвестным переменным произвольные значения. Из полученной системы линейных уравнений находим основные неизвестные переменные методом Крамера, матричным методом или методом Гаусса.
Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.
Методом Гаусса можно решать системы линейных алгебраических уравнений любого вида без предварительного их исследования на совместность. Процесс последовательного исключения неизвестных переменных позволяет сделать вывод как о совместности, так и о несовместности СЛАУ, а в случае существования решения дает возможность отыскать его.
С точки зрения вычислительной работы метод Гаусса является предпочтительным.
Смотрите его
подробное описание
и разобранные примеры в статье метод Гаусса для решения систем линейных алгебраических уравнений общего вида .
Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.
В этом разделе речь пойдет о совместных однородных и неоднородных системах линейных алгебраических уравнений, имеющих бесконечное множество решений.
Разберемся сначала с однородными системами.
Фундаментальной системой решенийоднородной системы из p
линейных алгебраических уравнений с n
неизвестными переменными называют совокупность (n – r)
линейно независимых решений этой системы, где r
– порядок базисного минора основной матрицы системы.
Если обозначить линейно независимые решения однородной СЛАУ как X (1) , X (2) , …, X (n-r)
(X (1) , X (2) , …, X (n-r)
– это матрицы столбцы размерности n
на 1
), то общее решение этой однородной системы представляется в виде линейной комбинации векторов фундаментальной системы решений с произвольными постоянными коэффициентами С 1 , С 2 , …, С (n-r)
, то есть, .
Что обозначает термин общее решение однородной системы линейных алгебраических уравнений (орослау)?
Смысл прост: формула задает все
возможные решения
исходной СЛАУ, другими словами, взяв любой набор значений произвольных постоянных С 1 , С 2 , …, С (n-r)
, по формуле мы получим одно из решений исходной однородной СЛАУ.
Таким образом, если мы найдем фундаментальную систему решений, то мы сможем задать все решения этой однородной СЛАУ как .
Покажем процесс построения фундаментальной системы решений однородной СЛАУ.
Выбираем базисный минор исходной системы линейных уравнений, исключаем все остальные уравнения из системы и переносим в правые части уравнений системы с противоположными знаками все слагаемые, содержащие свободные неизвестные переменные. Придадим свободным неизвестным переменным значения 1,0,0,…,0
и вычислим основные неизвестные, решив полученную элементарную систему линейных уравнений любым способом, например, методом Крамера. Так будет получено X (1)
— первое решение фундаментальной системы. Если придать свободным неизвестным значения 0,1,0,0,…,0
и вычислить при этом основные неизвестные, то получим X (2)
. И так далее. Если свободным неизвестным переменным придадим значения 0,0,…,0,1
и вычислим основные неизвестные, то получим X (n-r)
. Так будет построена фундаментальная система решений однородной СЛАУ и может быть записано ее общее решение в виде .
Для неоднородных систем линейных алгебраических уравнений общее решение представляется в виде , где — общее решение соответствующей однородной системы, а — частное решение исходной неоднородной СЛАУ, которое мы получаем, придав свободным неизвестным значения 0,0,…,0
и вычислив значения основных неизвестных.
Разберем на примерах.
Пример.
Найдите фундаментальную систему решений и общее решение однородной системы линейных алгебраических уравнений
.
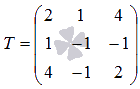
Решение.
Ранг основной матрицы однородных систем линейных уравнений всегда равен рангу расширенной матрицы. Найдем ранг основной матрицы методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмем элемент a 1 1 = 9
основной матрицы системы. Найдем окаймляющий ненулевой минор второго порядка:
Минор второго порядка, отличный от нуля, найден. Переберем окаймляющие его миноры третьего порядка в поисках ненулевого:
Все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг основной и расширенной матрицы равен двум.
Базисным минором возьмем . Отметим для наглядности элементы системы, которые его образуют:
Третье уравнение исходной СЛАУ не участвует в образовании базисного минора, поэтому, может быть исключено:
Оставляем в правых частях уравнений слагаемые, содержащие основные неизвестные, а в правые части переносим слагаемые со свободными неизвестными:
Построим фундаментальную систему решений исходной однородной системы линейных уравнений. Фундаментальная система решений данной СЛАУ состоит из двух решений, так как исходная СЛАУ содержит четыре неизвестных переменных, а порядок ее базисного минора равен двум. Для нахождения X (1)
придадим свободным неизвестным переменным значения x 2 = 1, x 4 = 0
, тогда основные неизвестные найдем из системы уравнений
.
Решим ее методом Крамера:
Таким образом, .
Теперь построим X (2)
. Для этого придадим свободным неизвестным переменным значения x 2 = 0, x 4 = 1
, тогда основные неизвестные найдем из системы линейных уравнений
.
Опять воспользуемся методом Крамера:
Получаем .
Так мы получили два вектора фундаментальной системы решений и , теперь мы можем записать общее решение однородной системы линейных алгебраических уравнений:
, где C 1
и C 2
– произвольные числа.
, равны нулю. Также примем минор в качестве базисного, исключим третье уравнение из системы и перенесем слагаемые со свободными неизвестными в правые части уравнений системы:
Для нахождения придадим свободным неизвестным переменным значения x 2 = 0 и x 4 = 0
, тогда система уравнений примет вид
, откуда методом Крамера найдем основные неизвестные переменные:
Имеем
, следовательно,
где C 1
и C 2
– произвольные числа.
Следует заметить, что решения неопределенной однородной системы линейных алгебраических уравнений порождают
линейное пространство
Решение.
Каноническое уравнение эллипсоида в прямоугольной декартовой системе координат имеет вид
. Наша задача состоит в определении параметров a
, b
и с
. Так как эллипсоид проходит через точки А
, В
и С
, то при подстановке их координат в каноническое уравнение эллипсоида оно должно обращаться в тождество. Так мы получим систему из трех уравнений:
Обозначим
, тогда система станет системой линейных алгебраических уравнений
.
Вычислим определитель основной матрицы системы:
Так как он отличен от нуля, то решение мы можем найти методом Крамера:
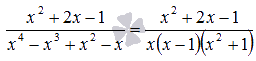
). Очевидно, что x = 0
и x = 1
являются корнями этого многочлена. Частным от деления
на
является . Таким образом, имеем разложение и исходное выражение примет вид
.
Воспользуемся методом неопределенных коэффициентов.
Приравняв соответствующие коэффициенты числителей, приходим к системе линейных алгебраических уравнений
. Ее решение даст нам искомые неопределенные коэффициенты А
, В
, С
и D
.
Решим систему методом Гаусса:
При обратном ходе метода Гаусса находим D = 0, C = -2, B = 1, A = 1
.
Получаем,
Ответ:
.
Системы уравнений получили широкое применение в экономической отрасли при
математическом моделировании
различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.
Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.
Опыт других людей
Система линейных алгебраических уравнений — это основа многих математических и инженерных расчетов. Люди отмечают, что решение таких систем позволяет моделировать и анализировать различные явления в природе, экономике и технике. Они отмечают, что умение работать с системами линейных уравнений является важным навыком для специалистов в различных областях. Также отмечается, что системы линейных уравнений широко применяются в компьютерных технологиях, физике, экономике и других областях, что подчеркивает их значимость и актуальность в современном мире.

Линейное уравнение
Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.
Виды систем линейных уравнений
Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.
Решить систему уравнений
—
это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или решения не существует их называют равносильными.
Однородными системами линейных уравнений являются системы
правая часть
которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.
Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.
Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.
Основная задача при обучении способам решения — это научить правильно анализировать систему и находить
оптимальный алгоритм
решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем решение примера системы линейных уравнений 7 класса методом подстановки:
Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y.
Последний шаг
это проверка полученных значений.
Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:
Решение с помощью алгебраического сложения
При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на
различные числа
. Конечной целью математических действий является уравнение с одной переменной.
Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
- Почленно сложить полученное выражение и найти одно из неизвестных.
- Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.
Способ решения введением новой переменной
Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.
Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.
Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В
заданном примере
a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Решение для полученных в итоге системы находят методом сложения.
Наглядный метод решения систем
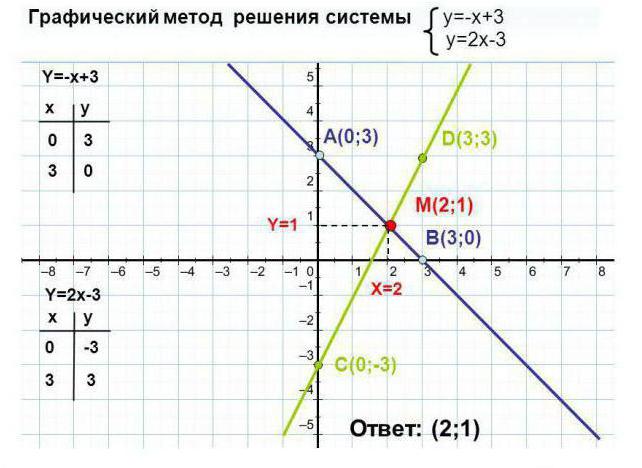
Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.
Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n — строк и m — столбцов.
Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей — вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Обратная матрица — это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.
Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.
Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Решение примеров систем линейных уравнений матричным методом
Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.
В примере a nm — коэффициенты уравнений, матрица — вектор x n — переменные, а b n — свободные члены.
Решение систем методом Гаусса
В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.
После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:
Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .
Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.
Метод Гаусса труден для восприятия учеников
средней школы
, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.
Для простоты записи вычислений принято делать следующим образом:
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.
В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
Возможно, будет полезно почитать:
- Заявление о приостановке работы в связи с невыплатой зарплаты
; - Что сказано об увольнении по собственному желанию в п
; - Как восстановить утерянную квитанцию Потерял чек сбербанка можно ли восстановить
; - Где взять номер лицевого счета для заявления на налоговый вычет?
; - Порядок заполнения перечня заявлений о ввозе товаров и уплате косвенных налогов Проверить уплату косвенных налогов в белоруссии
; - Поиск инн организации по названию
; - Дистанционное обучение на бухгалтерских курсах
; - Измерение величин Измеряется s в физике
;
Частые вопросы
Какие бывают системы линейных алгебраических уравнений?
Если система линейных уравнений имеет хотя бы одно решение, то ее называют совместной. Система линейных уравнений, не имеющая решений, называется несовместной. Система, имеющая единственное решение, называется определенной. Система, имеющая множество решений, называется неопределенной.
Что такое система уравнений простыми словами?
Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться, такую группу уравнений мы называем системой.
Как правильно решать линейные уравнения?
правая и левая части каждого уравнения почленно складываются, получается уравнение с одной переменной, полученное уравнение решается относительно единственной переменной, значение найденной переменной подставляется в одно из исходных уравнений системы, далее определяется значение второй переменной.
Как записать ответ в системе уравнений?
Ответ принято записывать в виде тройки значений (x, y, z). Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Полезные советы
СОВЕТ №1
При решении системы линейных алгебраических уравнений используйте метод Гаусса для приведения матрицы коэффициентов к ступенчатому виду. Это упростит процесс решения системы.
СОВЕТ №2
Не забывайте проверять полученное решение подстановкой в исходную систему уравнений, чтобы исключить возможные ошибки.
СОВЕТ №3
Если система имеет бесконечное количество решений, попробуйте выразить решение через параметры или воспользуйтесь методом Крамера для нахождения общего решения.