О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.
История египетского треугольника
Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.
Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.
Мнение эксперта:
Египетский треугольник – это особый вид прямоугольного треугольника, у которого длины сторон образуют простые числа. Это означает, что стороны треугольника могут быть выражены целыми числами, что делает его особенно интересным для математических исследований.
Мнение экспертов по вопросу о равенстве сторон египетского треугольника различно. Некоторые математики считают, что стороны такого треугольника могут быть равны любым целым числам, при условии их взаимной простоты. Другие эксперты утверждают, что стороны египетского треугольника всегда могут быть выражены в виде (m^2 — n^2), (2mn) и (m^2 + n^2), где m и n – взаимно простые числа, а их разность – нечетное число.
Что касается обратной теоремы Пифагора, то для египетского треугольника она выглядит следующим образом: для любого египетского треугольника с катетами a и b и гипотенузой c справедливо равенство a^2 + b^2 = c^2.
Таким образом, мнения экспертов по вопросу о равенстве сторон египетского треугольника и его связи с обратной теоремой Пифагора различны, и данная тема требует дальнейших исследований и обсуждений в математическом сообществе.

Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника.
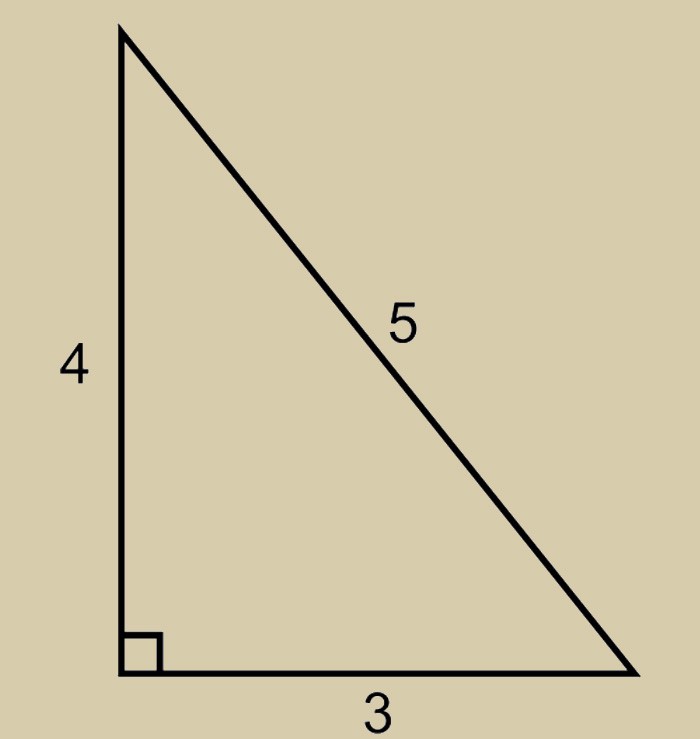
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Внимание
! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов.
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
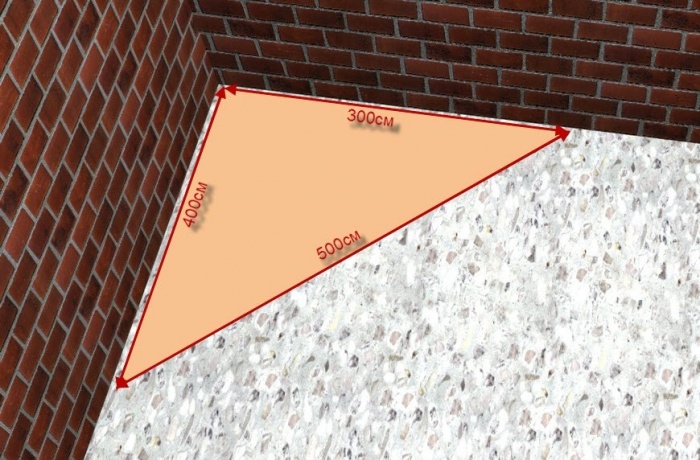
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.
Внимание
! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам.
Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше,
наилучшим вариантом
будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении
прямого угла
помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
Как получить египетский треугольник при помощи верёвки
Свойства этой
геометрической фигуры
тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
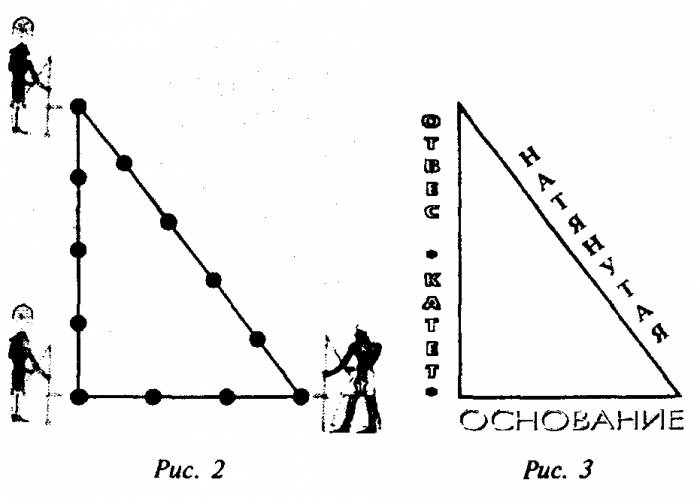
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Важно
! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Внимание
! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках.
Интересные факты
- Египетский треугольник — это прямоугольный треугольник со сторонами 3, 4 и 5.Это самый простой из всех прямоугольных треугольников, и он имеет ряд интересных свойств. Например, его площадь равна половине произведения его катетов, а его гипотенуза равна сумме его катетов.
- Египетский треугольник является единственным прямоугольным треугольником, стороны которого являются целыми числами.Это делает его очень удобным для использования в различных математических задачах и приложениях. Например, египетский треугольник часто используется для построения прямых углов и для измерения расстояний.
- Обратная теорема Пифагора утверждает, что если стороны прямоугольного треугольника являются целыми числами, то его гипотенуза также является целым числом.Это утверждение является обобщением теоремы Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Обратная теорема Пифагора имеет ряд интересных следствий. Например, она позволяет нам найти все прямоугольные треугольники со сторонами, которые являются целыми числами.
https://youtube.com/watch?v=eiugKlEtZuo
Итоги
Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.
Ка-ж-дый, кто внимательно слушал в школе преподавателя геометрии, очень хорошо знаком с тем, что представляет собой египетский треугольник. От других видов подобных с углом в 90 градусов он отличается особым соотношением сторон. Когда человек впервые слышит словосочетание «египетский треугольник», на ум приходят картины величественных пирамид и фараонов. А что же говорит история?
Как это всегда бывает, в отношении названия «египетский треугольник» есть несколько теорий. Согласно одной из них, известная теорема Пифагора увидела свет именно благодаря данной фигуре. В 535 году до н.э. Пифагор, следуя рекомендации Фалеса, отправился в Египет с целью восполнить некоторые пробелы в познаниях математики и астрономии. Там он обратил внимание на особенности работы египетских землемеров. Они очень
необычным способом
выполняли построение с прямым углом, стороны которой были взаимосвязаны одна с другой соотношением 3-4-5. Данный математический ряд позволял относительно легко связать квадраты всех трех сторон одним правилом. Именно так и возникла знаменитая теорема. А египетский треугольник как раз и есть та самая фигура, натолкнувшая Пифагора на гениальнейшее решение. Согласно другим историческим данным, фигуре дали название греки: в то время они часто гостили в Египте, где могли заинтересоваться работой землемеров. Существует вероятность, что, как это часто бывает с научными открытиями, обе истории произошли одновременно, поэтому нельзя с уверенностью утверждать, кто же придумал первым название «египетский треугольник». Свойства его удивительны и, разумеется, не исчерпываются одним лишь соотношением размеров сторон. Его площадь и стороны представлены целыми числами. Благодаря этому применение к нему теоремы Пифагора позволяет получить целые числа квадратов гипотенузы и катетов: 9-16-25. Конечно, это может быть простым совпадением. Но как в таком случае объяснить тот факт, что египтяне считали «свой» треугольник священным? Они верили в его взаимосвязь со всей Вселенной.
После того, как информация об этой необычной геометрической фигуре стала общедоступной, в мире начались поиски других подобных треугольников с целочисленными сторонами. Было очевидно, что они существуют. Но важность вопроса состояла не в том, чтобы просто выполнить математические расчеты, а проверить «священные» свойства. Египтяне, при всей своей необычности, никогда не считались глупыми — ученые до сих пор не могут объяснить, как именно были возведены пирамиды. А здесь, вдруг, обычной фигуре приписывалась связь с Природой и Вселенной. И, действительно, найденная клинопись содержит указания о подобном треугольнике со стороной, размер которой описывается 15-значным числом. В настоящее время египетский треугольник, углы которого равны 90 (прямой), 53 и 37 градусов, находят в совершенно неожиданных местах. К примеру, при изучении поведения молекул самой обыкновенной воды, выяснилось, что смена сопровождается перестройкой пространственной конфигурации молекул, в которой можно увидеть…тот самый египетский треугольник. Если вспомнить, что состоит из трех атомов, то можно говорить об условных трех сторонах. Конечно, о полном совпадении знаменитого соотношения речь не идет, но получаемые числа очень и очень близки к искомым. Не потому ли египтяне признавали за своим «3-4-5» треугольником символический ключ к
природным явлениям
и тайнам Вселенной? Ведь вода, как известно, основа жизни. Без сомнения, еще слишком рано ставить точку в изучении знаменитой египетской фигуры. Наука никогда не спешит с выводами, стремясь доказать свои предположения. А нам же остается лишь ждать и удивляться знаниям
У каждой науки есть свой фундамент, на основании которого и строится все последующее ее развитие. В это, безусловно, теорема Пифагора. Со школьной скамьи учат формулировке: «Пифагоровы штаны во все стороны равны». По научному звучит немного , менее красноречиво. Наглядно эта теорема представляется в со сторонами 3-4-5. Это и есть замечательный Египетский треугольник.
Опыт других людей
Египетский треугольник вызывает интерес у многих людей. Одни утверждают, что его стороны соотносятся как 3:4:5, другие утверждают, что это не всегда так. Однако обратная теорема Пифагора позволяет нам легко вычислить длины сторон этого треугольника, если известна его площадь. Это делает его особенно полезным в геометрии и строительстве.

История
Знаменитый греческий математик и философ Пифагор Самосский, давший свое имя теореме, жил 2,5 тыс. лет назад. Биография этого выдающегося ученого мало изучена, однако до сегодняшнего времени все же дошли некоторые .
По просьбе Фалеса, с целью изучения математики и астрономии, в 535 году до нашей эры он отправился в длинное путешествие в Египет и Вавилон. В Египте среди бескрайнего простора пустыни он увидел величественные пирамиды, изумляющие своими огромными размерами и стройными геометрическими формами. Стоит отметить, что Пифагор их лицезрел в несколько ином виде, чем тот, в котором видят туристы сейчас. Это были невообразимо огромные для того времени сооружения с четкими ровными гранями на фоне прилегающих храмов поменьше, для жен, детей и других родственников фараона. Кроме прямого назначения (усыпальницы и хранителя священного тела фараона) пирамиды сооружались и как символы величия, богатства и могущества Египта.
И вот Пифагор в ходе тщательного изучения этих конструкций заметил строгую закономерность в соотношении размеров и форм сооружений. Размерам Египетского треугольника соответствует пирамида Хеопса, она считалась священной и носила особенный магический смысл.
Пирамида Хеопса есть достоверное подтверждение тому, что знание о пропорциях египетского треугольника использовалась египтянами задолго до открытия Пифагора.
Применение
Форма у треугольника самая простая и гармоничная, с ним легко работать, для этого потребуются лишь самые незатейливые инструменты — циркуль и линейка.
Без применения специальных инструментов построить прямой угол практически невозможно. Но задание сильно упрощается при использовании знаний о египетском треугольнике. Для этого берут простую веревку, разделяют ее на 12 частей и складывают в форме треугольника с пропорциями 3-4-5. Угол между 3 и 4 получится прямым. В далеком прошлом этот треугольник активно использовали архитекторы и землемеры.
Не исключено, что, термин «Египетский треугольник» дал
Пифагор, побывав по настоянию
Фалесав Египте…
«… в данном очерке нас интересует именно непрактический, неприкладной аспект математики, мы предполагаем весьма и весьма поучительным включение в «джентльменский набор» математических представлений знание того, почему треугольник со сторонами 3, 4, 5 назывется египетским.
А всё дело в том, что древнеегипетские строители пирамид нуждались в способе построения прямого угла. Вот требуемый способ. Веревка разбивается на 12 равных частей, границы между соседними частями помечаются, а концы верёвки соединяются. Затем верёвка натягивается тремя людьми так, чтобы она образовала треугольник, а расстояния между соседними натягивателями составляли бы, соответственно, 3 части, 4 части и 5 частей. В таком случае треугольник окажется прямоугольным, в коем стороны 3 и 4 будут катетами, а сторона 5 — гипотенузой, так что угол между сторонами 3 и 4 будет прямым.
Боюсь, что большинство читателей в ответ на вопрос «Почему треугольник окажется прямоугольным?» сошлётся на теорему Пифагора: ведь три в квадрате плюс четыре в квадрате равно пяти в квадрате. Однако теорема Пифагора утверждает, что если треугольник прямоугольный, то в этом случае сумма квадратов двух его сторон равна квадрату третьей.
Здесь же используется теорема, обратная к теореме Пифагора: если сумма квадратов двух сторон треугольника равна квадрату третьей, то в этом случае треугольник прямоугольный. (Не уверен, что эта обратная теорема занимает должное место в школьной программе.)».
Успенский В.А. , Апология математики, или о математике как части духовной культуры, журнал «
Новый мир
», 2007 г., N 11, с. 131.
Известный математик Пифагор совершил множество различных открытий, но большинству людей, которым не приходится регулярно сталкиваться с алгеброй и геометрией, он известен благодаря своей теореме. Ученый открыл ее, пребывая в Египте, где его очаровала красота и изящность пирамид, а это, в свою очередь, натолкнуло его на мысль о том, что в их формах прослеживается определенная закономерность.
История открытия
Своим названием египетский треугольник обязан эллинам, которые часто посещали Египет в VII-V веках до н. э., среди них был и Пифагор. Основой пирамиды Хеопса является прямоугольный многоугольник, а
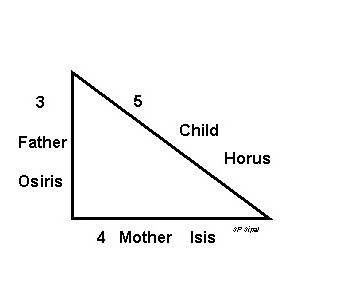
пирамиды Хефрена — так называемый египетский треугольник, который древние называли священным. Плутарх писал, что жители Египта соотносили природу с этой геометрической фигурой: вертикальный катет символизировал мужчину, основание — женщину, а гипотенуза — ребенка. Соотношение сторон в нем равно 3:4:5, а это приводит к теореме Пифагора, так как 3 2 х 4 2 = 5 2 . Следовательно, тот факт, что в основании пирамиды Хефрена лежит египетский треугольник, позволяет утверждать, что знаменитая теорема была известна жителям
древнего мира
еще до того, как ее сформулировал Пифагор. Особенностью этой фигуры также считается то, что благодаря такому соотношению сторон она является первым и простейшим из Героновых треугольников, поскольку ее стороны и площадь целочисленные.
Применение
Египетский треугольник с древности пользовался популярностью в архитектуре и строительстве.
В основном он использовался тогда, когда строили прямые углы с помощью шнура или веревки, разделенной на 12 частей. По отметкам на такой веревке можно было очень точно создать прямоугольную фигуру, катеты которой будут служить направляющими для установки прямого угла строения. Известно, что такие свойства этой геометрической фигуры использовались не только в Древнем Египте, но и, задолго до этого, в Китае, Вавилоне и Месопотамии. Для создания пропорциональных сооружений в Средние века также использовался египетский треугольник.
Углы
Соотношение сторон этого треугольника 3:4:5 приводит к тому, что он является прямоугольным, т. е. один угол равен 90 градусам, а два других — 53,13 и 36,87 градусам. Прямым является угол между сторонами, соотношение которых равно 3:4.
Доказательство
При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3 2 х 4 2 = 5 2 , следовательно, он является прямоугольным.
Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.
Возможно, будет полезно почитать:
- Заявление о приостановке работы в связи с невыплатой зарплаты
; - Что сказано об увольнении по собственному желанию в п
; - Как восстановить утерянную квитанцию Потерял чек сбербанка можно ли восстановить
; - Где взять номер лицевого счета для заявления на налоговый вычет?
; - Порядок заполнения перечня заявлений о ввозе товаров и уплате косвенных налогов Проверить уплату косвенных налогов в белоруссии
; - Поиск инн организации по названию
; - Дистанционное обучение на бухгалтерских курсах
; - Измерение величин Измеряется s в физике
;
Частые вопросы
Чему равны стороны египетского треугольника?
Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.
Чему равен египетский треугольник?
Египетский треугольник – известная с античности геометрическая фигура, стороны которой соотносятся согласно пропорции 3:4:5. В соответствии с обратной теоремой Пифагора, этот треугольник имеет прямой угол.
Чему равны углы в треугольнике Пифагора?
В равнобедренном прямоугольном треугольнике углы при гипотенузе равны (180° — 90°) /2 = 45°. В равностороннем треугольнике все три угла совпадают и поэтому равны 180° / 3 = 60°. (Теорема о внешнем угле треугольника) Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Как связаны Пифагор и прямоугольный треугольник?
Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Полезные советы
СОВЕТ №1
Изучите историю и особенности египетского треугольника, чтобы понять его значение и применение в математике.
СОВЕТ №2
Изучите обратную теорему Пифагора и применение ее к египетскому треугольнику, чтобы лучше понять связь между этими математическими концепциями.