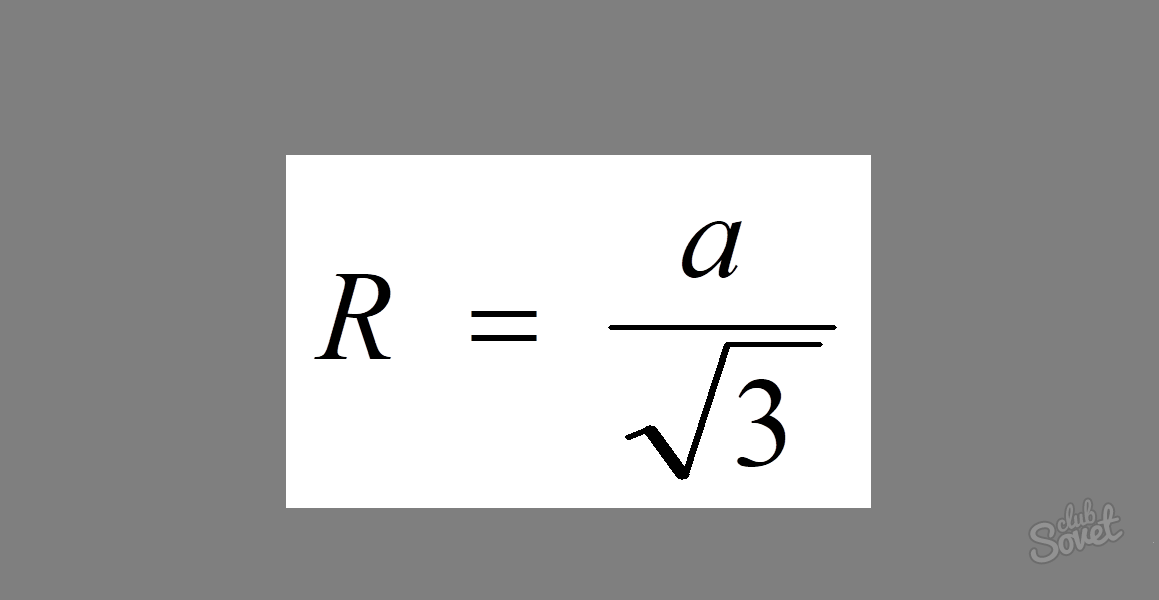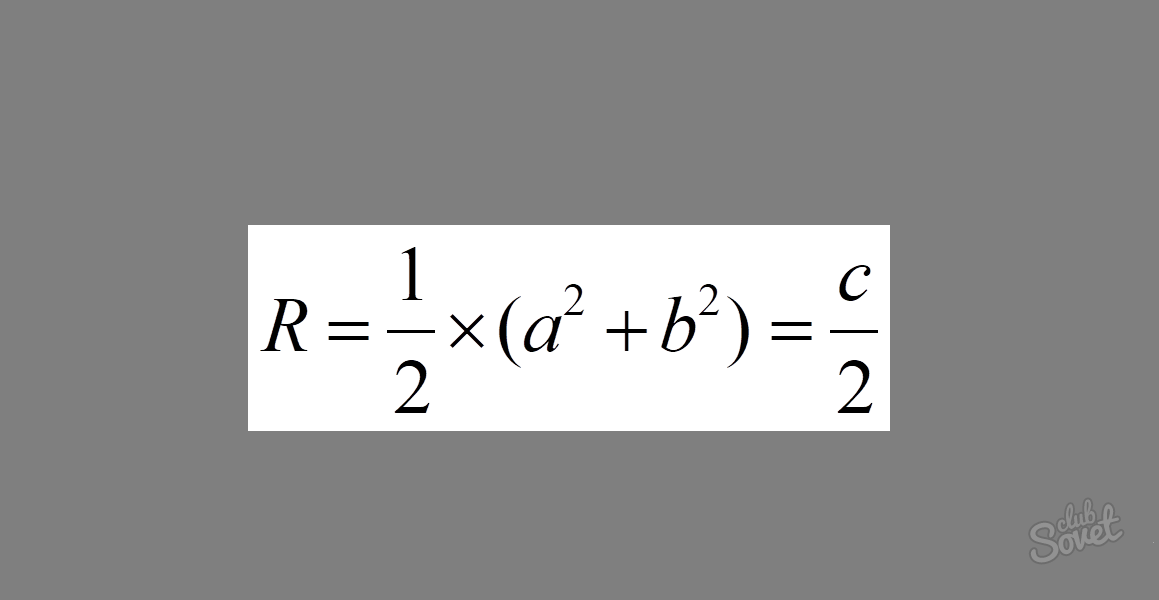Очень часто при решении геометрических задач приходится совершать действия со вспомогательными фигурами. Например, находить радиус вписанной или описанной окружности и т.д. Данная статья покажет, как находить радиус окружности, описанной около треугольника. Или, иными словами, радиус окружности, в которую вписан треугольник.
Как найти радиус окружности, описанной около треугольника — общая формула
Общая формула выглядит следующим образом: R = abc/4√p(p — a)(p — b)(p — c), где R — радиус описанной окружности, p — периметр треугольника поделенный на 2 (полупериметр). a, b, c —
стороны треугольника
.
Найти радиус описанной окружности треугольника, если a = 3, b = 6, c = 7.
Таким образом, исходя из вышеприведенной формулы, вычисляем полупериметр:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Подставляем значения в формулу и получаем:
R = 3 × 6 × 7/4√8(8 — 3)(8 — 6)(8 — 7) = 126/4√(8 × 5 × 2 × 1) = 126/4√80 = 126/16√5.
Ответ: R = 126/16√5
Мнение эксперта:
При рассмотрении вписанной и описанной окружностей в треугольнике, эксперты сходятся во мнении, что их центром является одна и та же точка. Эта точка называется центром описанной окружности и совпадает с центром вписанной окружности. Чтобы найти радиус окружности, описанной около треугольника, можно воспользоваться формулой: радиус описанной окружности равен половине произведения сторон треугольника, деленной на площадь треугольника. Это позволяет определить радиус окружности, описанной вокруг треугольника, и использовать эту информацию в дальнейших расчетах и анализе геометрических фигур.

Как найти радиус окружности, описанной около равностороннего треугольника
Для нахождения радиуса окружности, описанной около
равностороннего треугольника
, существует довольно простая формула: R = a/√3, где a — величина его стороны.
Пример: Сторона равностороннего треугольника равна 5. Найти радиус описанной окружности.
Так как у равностороннего треугольника все стороны равны, для решения задачи нужно всего лишь вписать ее значение в формулу. Получим: R = 5/√3.
Ответ: R = 5/√3.
Интересные факты
- Центр вписанной окружности треугольника – это точка пересечения его биссектрис. Эта точка находится на одинаковом расстоянии от всех трех сторон треугольника.
- Центр описанной окружности треугольника – это точка пересечения его серединных перпендикуляров. Эта точка находится на одинаковом расстоянии от всех трех вершин треугольника.
- Радиус описанной окружности треугольника равен половине длины его диаметра. Диаметр описанной окружности треугольника – это отрезок, соединяющий две вершины треугольника и проходящий через его центр.

Как найти радиус окружности, описанной около прямоугольного треугольника
Формула выглядит следующим образом: R = 1/2 × √(a² + b²) = c/2, где a и b — катеты и c — гипотенуза. Если сложить квадраты катетов в
прямоугольном треугольнике
, то получим квадрат гипотенузы. Как видно из формулы, данное выражение находится под корнем. Вычислив корень из квадрата гипотенузы, мы получим саму длину. Умножение получившегося выражения на 1/2 в итоге приводит нас к выражению 1/2 × c = c/2.
Пример: Вычислить радиус описанной окружности, если катеты треугольника равны 3 и 4. Подставим значения в формулу. Получим: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2.5.
В данном выражение 5 — длина гипотенузы.
Ответ: R = 2.5.
Опыт других людей
При обсуждении центра вписанной и описанной окружности, люди часто выражают удивление тем, как легко можно найти радиус окружности, описанной вокруг треугольника. Один из способов – использовать формулу радиуса описанной окружности, которая составляет половину произведения сторон треугольника, деленного на площадь треугольника. Этот метод позволяет быстро и точно определить радиус описанной окружности, что вызывает восхищение у многих.

Как найти радиус окружности, описанной около равнобедренного треугольника
Формула выглядит следующим образом: R = a²/√(4a² — b²), где a — длина бедра треугольника и b — длина основания.
Пример: Вычислить радиус окружности, если его бедро = 7, а основание = 8.
Решение: Подставляем в формулу данные значения и получаем: R = 7²/√(4 × 7² — 8²).
R = 49/√(196 — 64) = 49/√132. Ответ можно записать прямо так.
Ответ: R = 49/√132
Онлайн ресурсы для вычисления радиуса окружности
Можно очень легко запутаться во всех этих формулах. Поэтому при необходимости можно воспользоваться
онлайн калькуляторами
, которые помогут вам в решении задач на нахождение радиуса. Принцип работы таких мини-программ очень прост. Подставляете значение стороны в соответствующее поле и получаете готовый ответ. Можно выбрать несколько вариантов округления ответа: до десятичных, сотых, тысячных и т.д.
>>Геометрия: Окружность, описанная около треугольника. Полные уроки
ТЕМА УРОКА:
Окружность, описанная около треугольника.
Цели урока:
- Углубить знания по теме «Описанная окружности в треугольниках»
Задачи урока:
- Систематизировать знания по этой теме
- Подготовиться к решению задач повышенной сложности.
План урока:
- Введение.
- Теоретическая часть.
- Для треугольника.
- Практическая часть.
Введение.
Тема «Вписанные и описанные окружности в треугольниках» является одной из самых сложных в курсе геометрии. На уроках ей уделяется очень мало времени.
Геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы.
Для успешного выполнения этих заданий необходимы твердые знания основных геометрических фактов и некоторый опыт в решении геометрических задач.
Теоретическая часть.
Описанная окружность многоугольника– окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать O) пересечения серединных перпендикуляров к сторонам многоугольника.
Свойства.
Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
Вокруг любого
правильного многоугольника
можно описать окружность.
Для треугольника.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Вокруг любого треугольника можно описать окружность, притом
только одну.
Её центром будет являться точка пересечения серединных перпендикуляров.
У остроугольного треугольника центр описанной окружности лежит
внутри, у тупоугольного –
вне треугольника, у прямоугольного –
на середине гипотенузы.
Радиус описанной окружности может быть найден по формулам:
Где:
a,b,c– стороны треугольника,
α– угол, лежащий против стороны a,
S– площадь треугольника.
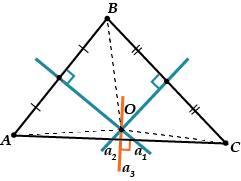
Доказать:
т.О – точка пересечения серединных перпендикуляров к сторонам ΔABC
Доказательство:
- ΔAОC – равнобедренный, т.к. ОА=ОС (как радиусы)
- ΔAОC – равнобедренный, перпендикуляр OD – медиана и высота, т.е. т.О лежит на серединном перпендикуляре к стороне АС
- Аналогично доказывается, что т.О лежит на серединных перпендикулярах к сторонам АВ и ВС
Что и требовалось доказать.
Замечание.
Прямую, проходящую через середину отрезка перпендикулярно к нему, часто называют серединным перпендикуляром. В связи с этим иногда говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Предмети > Математика > Математика 7 класс
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес
электронной почты
и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и
ближайших событиях
. - Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо – в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от
государственных органов
на территории РФ – раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности – включая административные, технические и физические – для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
В этой части мы обсудим окружность, описанную вокруг (часто говорят «около») треугольника. Прежде всего дадим определение.
1. Существование и центр описанной окружности
Тут возникает вопрос: а для всякого ли треугольника существует такая окружность? Вот оказывается, что да, для всякого. И более того, мы сейчас сформулируем теорему, которая ещё и отвечает на вопрос, где же находится центр описанной окружности.
Смотри, вот так:
Давай наберёмся мужества и докажем эту теорему. Если ты читал уже тему « » разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы. А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют. В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
Тут множество – это серединный перпендикуляр, а свойство « » – это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
Соединим с и с.Тогда линия является медианой и высотой в. Значит, – равнобедренный, – убедились, что любая точка, лежащая на серединном перпендикуляре, одинаково удалена от точек и.
Возьмём – середину и соединим и. Получилась медиана. Но – равнобедренный по условию не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка – точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
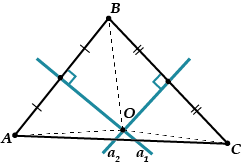
Рассмотрим треугольник. Проведём два серединных перпендикуляра и, скажем, к отрезкам и. Они пересекутся в какой-то точке, которую мы назовем.
А теперь, внимание!
Точка лежит на серединном перпендикуляре;
точка лежит на серединном перпендикуляре.
И значит, и.
Отсюда следует сразу несколько вещей:
Во – первых, точка обязана лежать на третьем серединном перпендикуляре, к отрезку.
То есть серединный перпендикуляр тоже обязан пройти через точку, и все три серединных перпендикуляра пересеклись в одной точке.
Во – вторых: если мы проведём окружность с центром в точке и радиусом, то эта окружность также пройдёт и через точку, и через точку, то есть будет описанной окружностью. Значит, уже есть, что пересечение трёх серединных перпендикуляров – центр описанной окружности для любого треугольника.
И последнее: о единственности. Ясно (почти), что точку можно получить единственным образом, поэтому и окружность – единственная. Ну, а «почти» – оставим на твоё размышление. Вот и доказали теорему. Можно кричать «Ура!».
А если в задаче стоит вопрос «найдите радиус описанной окружности»? Или наоборот, радиус дан, а требуется найти что – то другое? Есть ли формула, связывающая радиус описанной окружность с другими элементами треугольника?
Возможно, будет полезно почитать:
- Что написать в резюме в разделе «обо мне
; - Срок давности по неоплаченным кредитам: какой он
; - Психологическое понимание труда и профессии
; - Как испечь пасхальный кулич – рецепты к пасхе
; - Как испечь пасхальный кулич: мой семейный рецепт с подробными картинками
; - Пустынными тропами Аризоны
; - Пошаговый рецепт морковных оладий: фото и секреты
; - Сколько хранится фаршированный перец в холодильнике
;
Частые вопросы
Как найти радиус окружности, описанной около треугольника?
Радиус описанной около треугольника окружности можем найти по формуле: R = a / 2sinα, где а – сторона треугольника, α – противолежащий этой стороне угол.
Как определить центр окружности, описанной около треугольника?
Центр окружности описанной вокруг прямоугольного треугольника находится на середине гипотенузы. Нужно найти середину гипотенузы и провести перпендикуляр к гипотенузе, через эту середину. Этот перпендикуляр будет проходить через центр окружности.
Что является центром вписанной и описанной окружности?
Центром вписанной окружности является точка пересечения биссектрис. Около каждого треугольника можно описать окружность и при том только одну. Центром вписанной окружности является точка пересечения серединных перпендикуляров.
Как найти радиус описанной вписанной окружности?
Формулой вычисления радиуса вписанной окружности в прямоугольный треугольник является r = (a + b — c) / 2, где a и b – катеты треугольника.
Полезные советы
СОВЕТ №1
Центр вписанной окружности треугольника является точкой пересечения биссектрис его углов. Для нахождения центра вписанной окружности можно воспользоваться формулой для точки пересечения двух прямых.
СОВЕТ №2
Радиус окружности, описанной вокруг треугольника, можно найти, зная длины сторон треугольника, по формуле: \( R = \frac{abc}{4S} \), где \( a, b, c \) – длины сторон треугольника, а \( S \) – его площадь.