Действия с матрицами. Матрицы

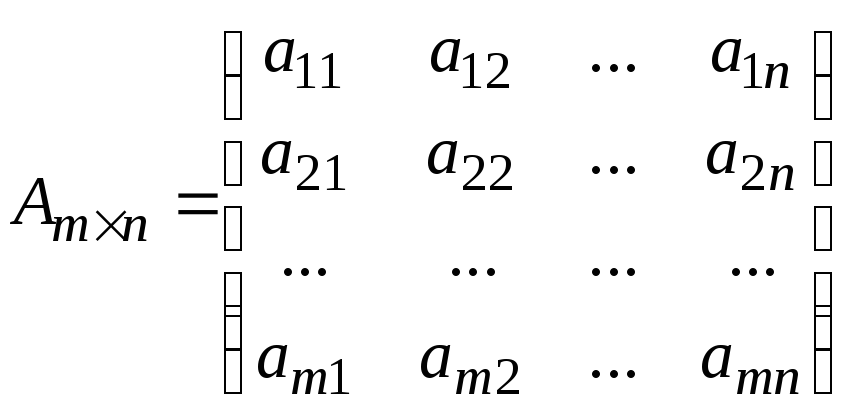
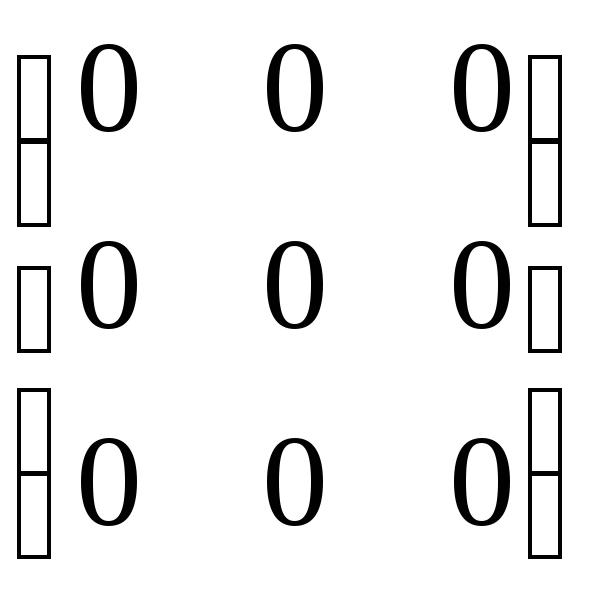
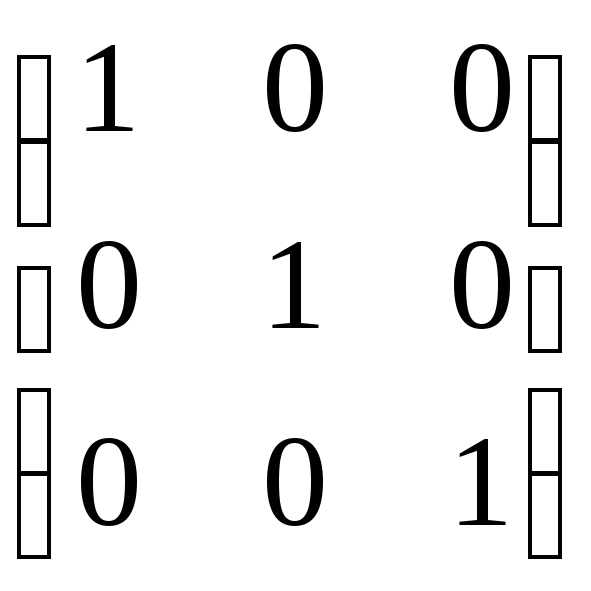
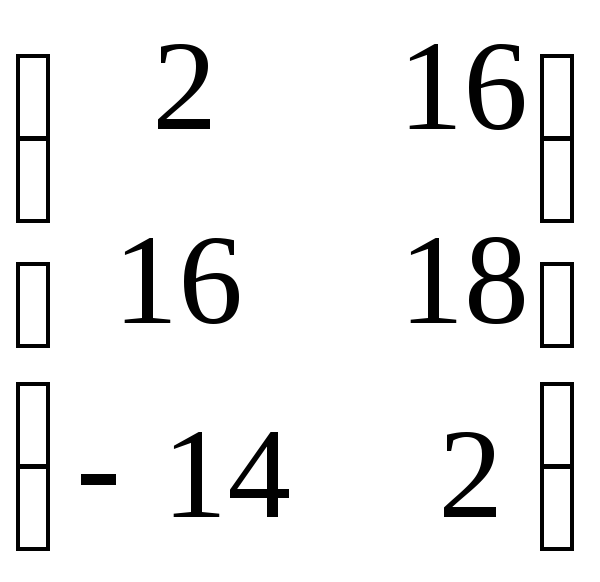
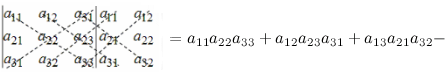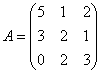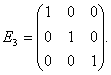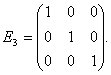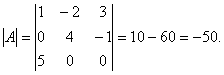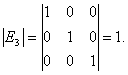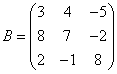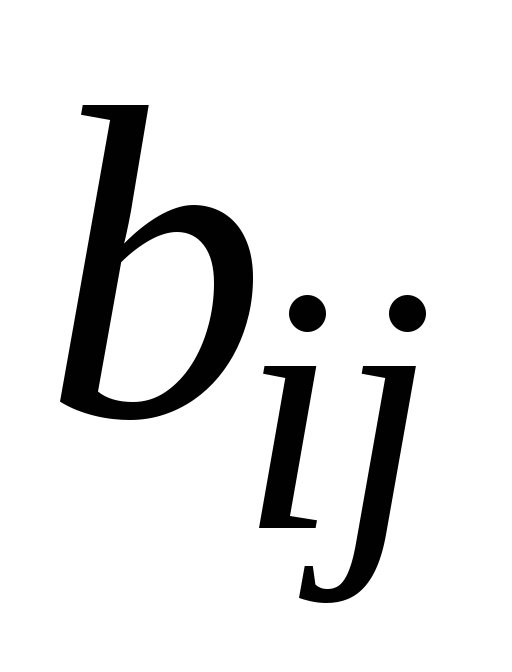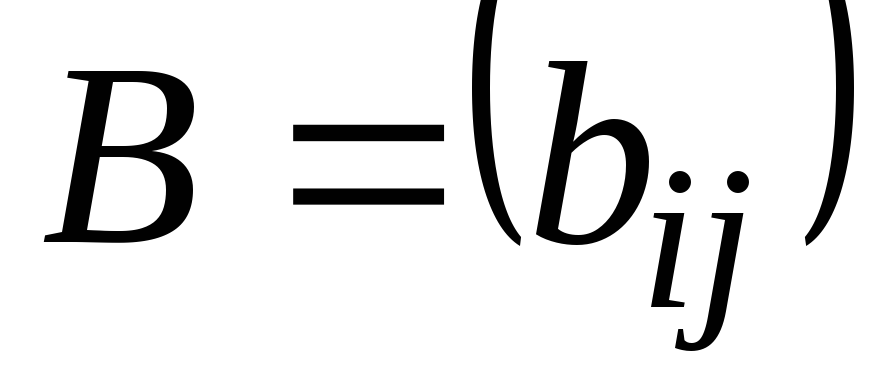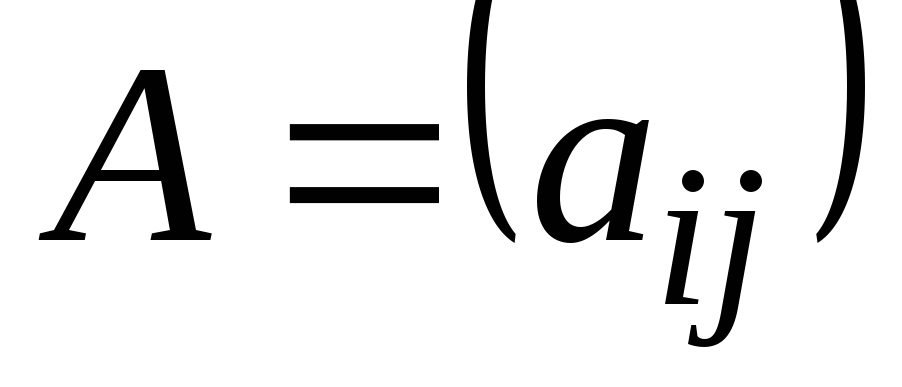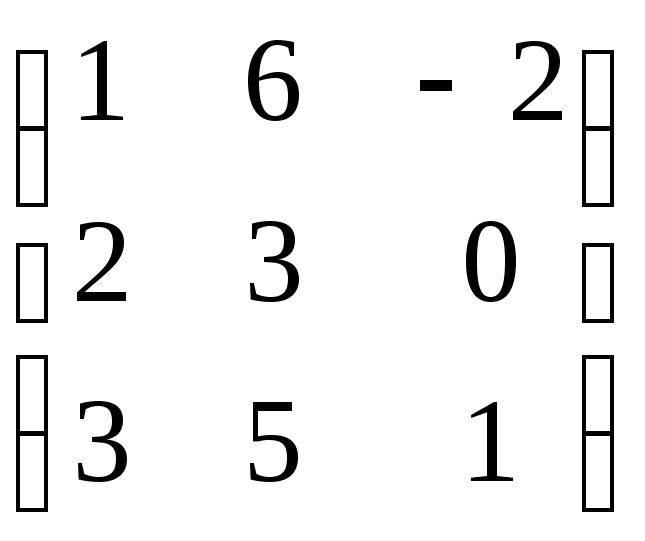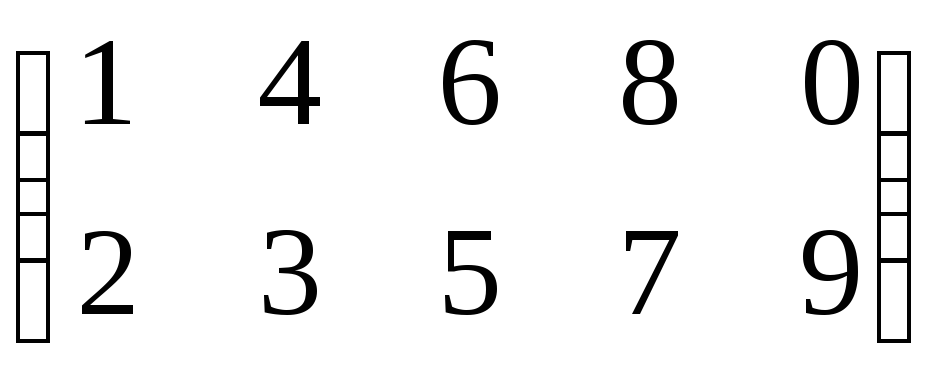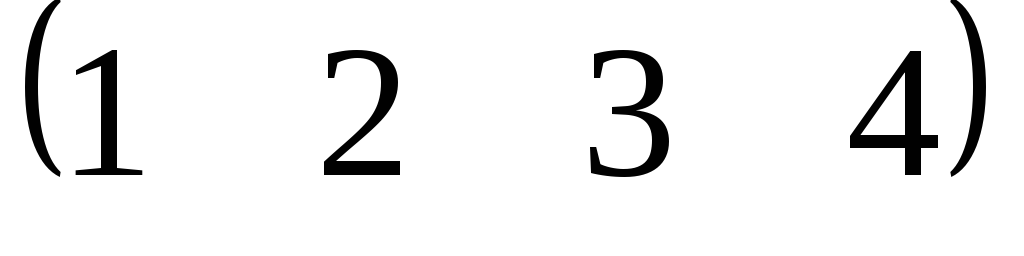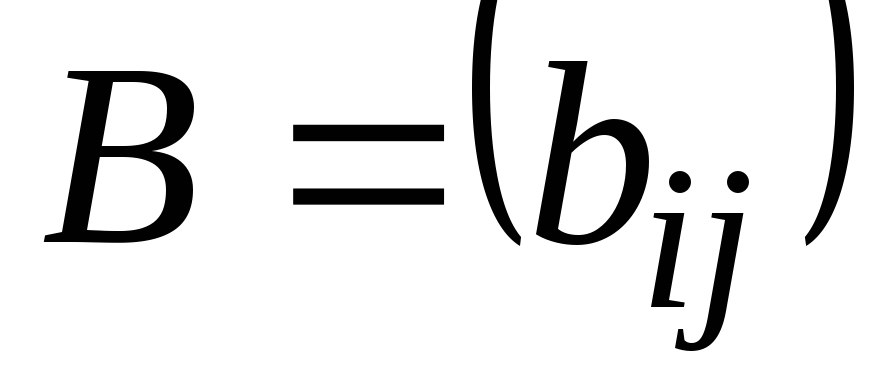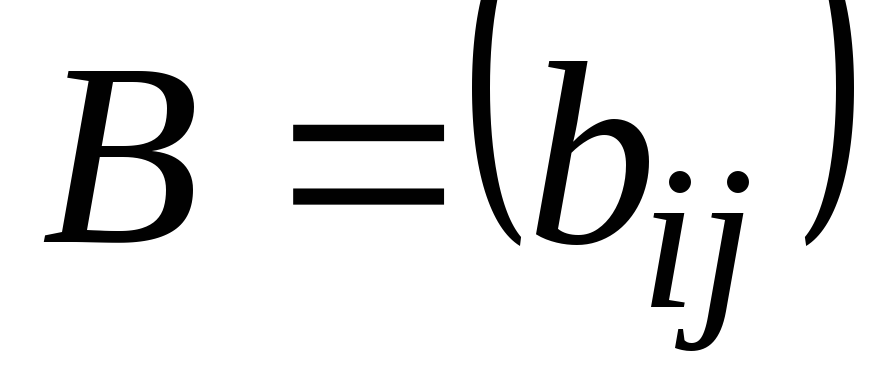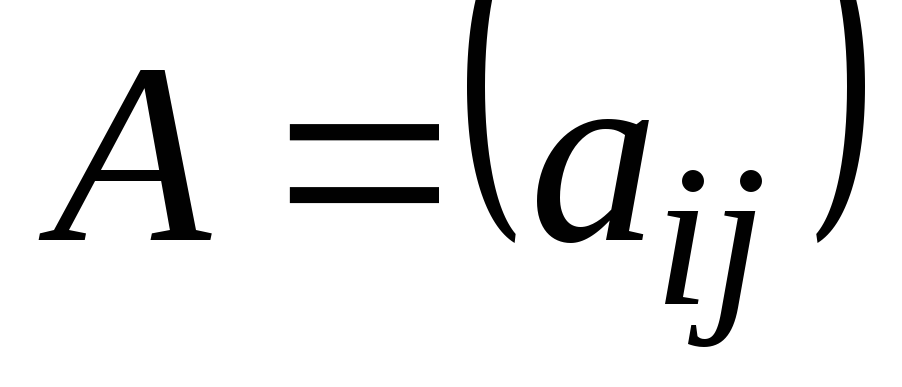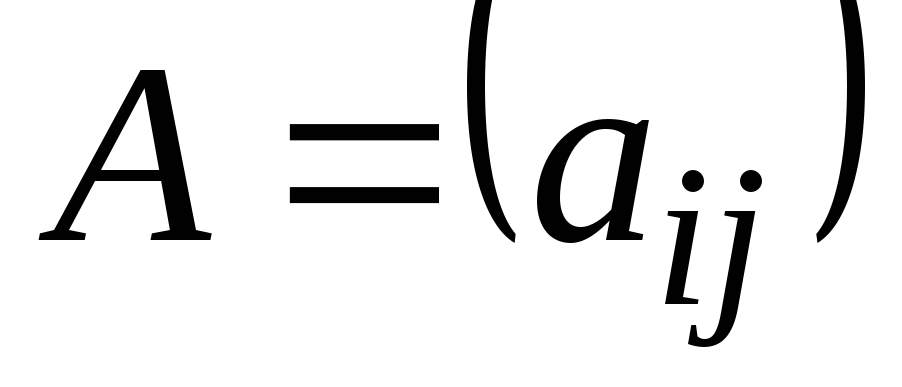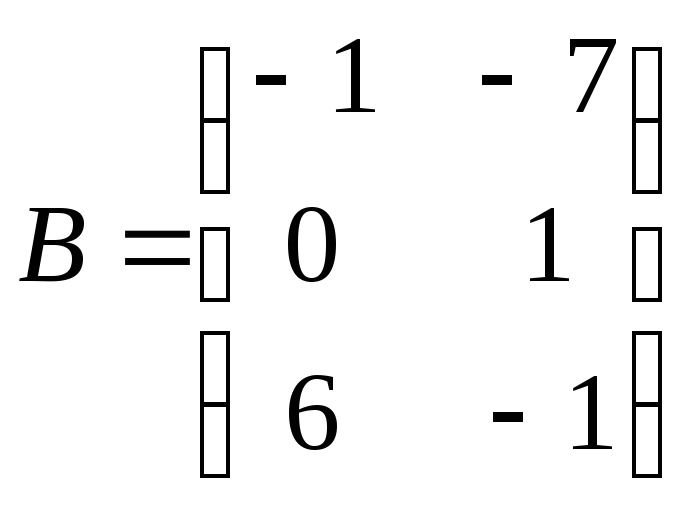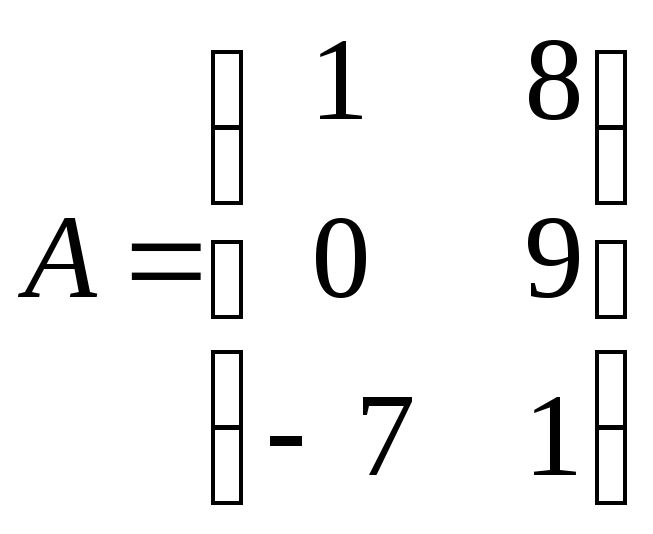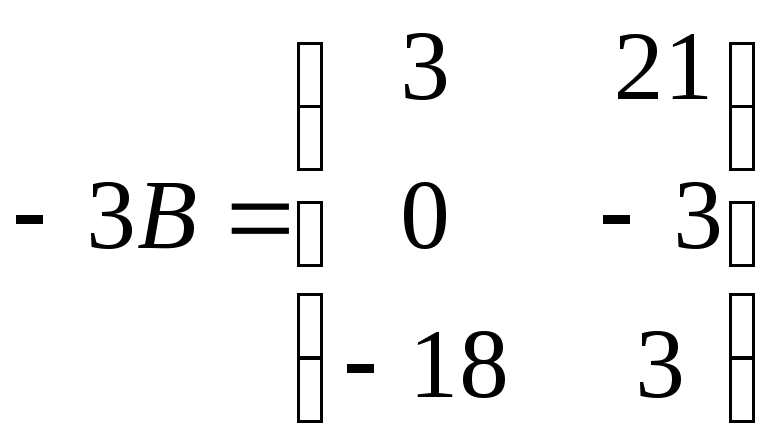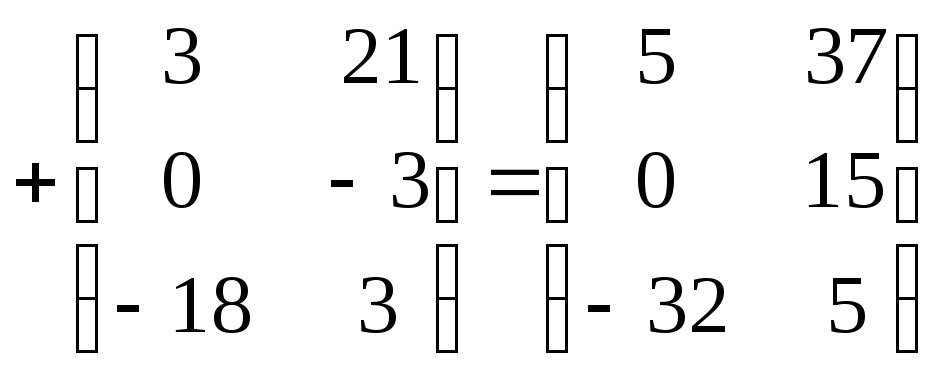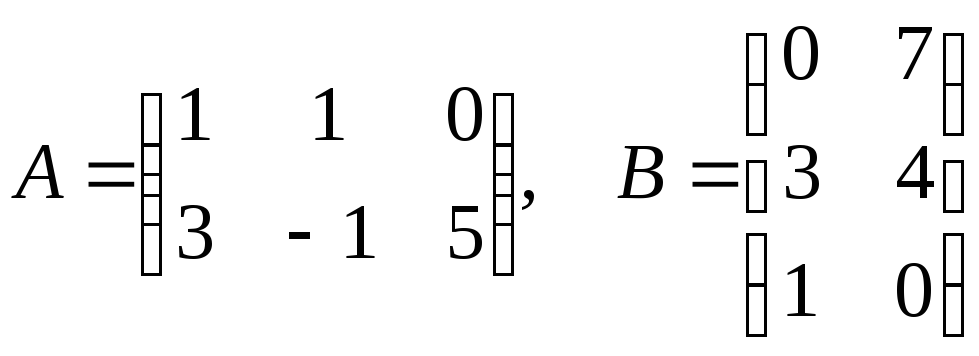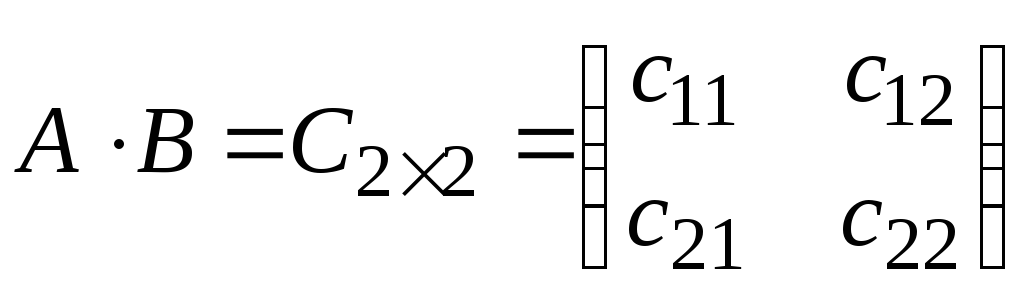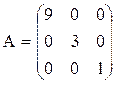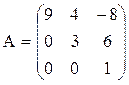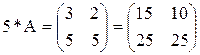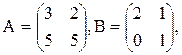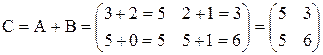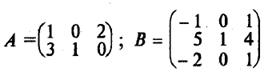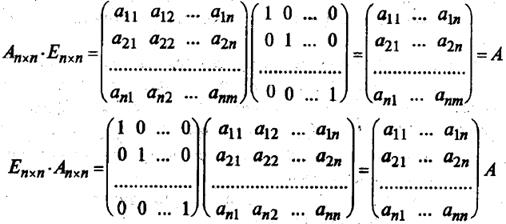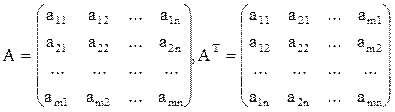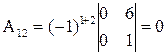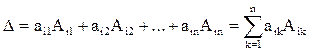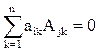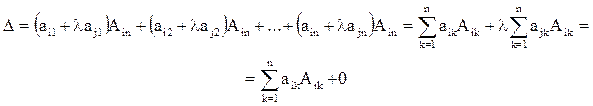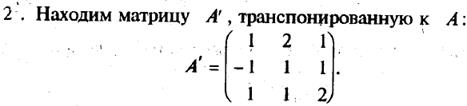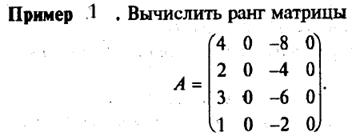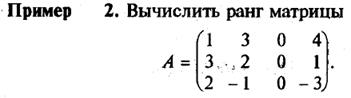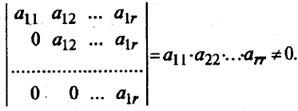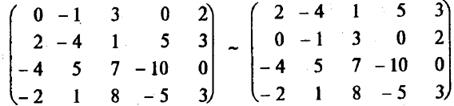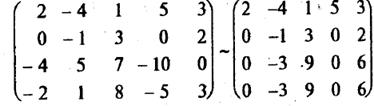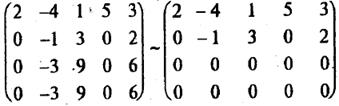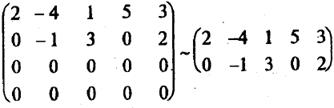Это понятие, которое обобщает все возможные операции, производимые с матрицами. Математическая матрица – таблица элементов. О такой таблице, где

mстрок и

nстолбцов, говорят, что это матрица имеет размерность

mна

n.

Общий вид матрицы:

Для

решения матрицнеобходимо понимать, что такое матрица и знать основные ее параметры. Основные элементы матрицы:

• Главная диагональ, состоящая из элементов
  
  а 11 ,а 22 …..а mn.
• Побочная диагональ, состоящая из элементов
  
  а 1n ,а 2n-1 …..а m1.

Основные виды матриц:

• Квадратная – такая матрица, где число строк = числу столбцов (
  
  m=n).
• Нулевая – где все элементы матрицы = 0.
• Транспонированная матрица — матрица
  
  В, которая была получена из исходной матрицы
  
  Aпутем замены строк на столбцы.
• Единичная – все элементы главной диагонали = 1, все остальные = 0.
• Обратная матрица — матрица, при умножении на которую исходная матрица даёт в результате единичную матрицу.

Матрица может быть симметричной относительно главной и побочной диагонали. Т.е., если

а 12 =а 21,

а 13 =а 31 ,….а 23 =а 32 …. а m-1n =а mn-1, то матрица симметрична относительно главной диагонали. Симметричными могут быть лишь квадратные матрицы.

Методы решения матриц.

Почти все

методы решения матрицызаключаются в нахождении ее определителя

n-го порядка и большинство из них довольно громоздки. Чтобы найти определитель 2го и 3го порядка есть другие, более рациональные способы.

Нахождение определителей 2-го порядка.

Для вычисления определителя матрицы

А2го порядка, необходимо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали:

Методы нахождения определителей 3го порядка.

Ниже приведены правила для нахождения определителя 3го порядка.

Упрощенно правило треугольника, как одного из

методов решения матриц, можно изобразить таким образом:

Другими словами, произведение элементов в первом определителе, которые соединены прямыми, берется со знаком “+”; так же, для 2го определителя – соответствующие произведения берутся со знаком “-“, то есть по такой схеме:

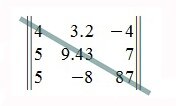
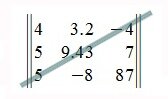
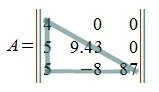
При

решении матриц правилом Саррюса, справа от определителя дописывают первые 2 столбца и произведения соответствующих элементов на главной диагонали и на диагоналях, которые ей параллельны, берут со знаком “+”; а произведения соответствующих элементов побочной диагонали и диагоналей, которые ей параллельны, со знаком “-“:

Разложение определителя по строке или столбцу при решении матриц.

Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку либо столбец, по которой/ому ведется разложение, будут обозначать стрелкой.

Приведение определителя к треугольному виду при решении матриц.

При

решении матрицметодом приведения определителя к треугольному виду, работают так: с помощью простейших преобразований над строками либо столбцами, определитель становится треугольного вида и тогда его значение, в соответствии со свойствами определителя, будет равно произведению элементов, которые стоят на главной диагонали.

Теорема Лапласа при решении матриц.

Решая матрицы по теореме Лапласа, необходимо знать непосредственно саму теорему. Теорема Лапласа: Пусть

Δ– это определитель

n-го порядка. Выбираем в нем любые

kстрок (либо столбцов), при условии

k
≤
n – 1. В таком случае сумма произведений всех миноров

k-го порядка, содержащихся в выбранных

kстроках (столбцах), на их алгебраические дополнения будет равна определителю.

Мнение эксперта:

Эксперты отмечают, что действия с матрицами играют важную роль в различных областях, включая математику, физику, информатику и экономику. Умение работать с матрицами необходимо для решения систем линейных уравнений, анализа данных, проектирования компьютерных график и многих других задач. По мнению специалистов, понимание операций над матрицами, таких как умножение, сложение, вычитание и нахождение определителя, является ключевым элементом успешного решения задач, связанных с линейной алгеброй и прикладными науками.

МАТРИЦЫ математика УМНОЖЕНИЕ МАТРИЦ и простейшие операции с матрицами

Решение обратной матрицы.

Последовательность действий для

решения обратной матрицы:

1. Понять, квадратная ли данная матрица. В случае отрицательного ответа становится ясно, что обратной матрицы для нее не может быть.
2. Вычисляем алгебраические дополнения.
3. Составляем союзную (взаимную, присоединённую) матрицу
   
   C.
4. Составляем обратную матрицу из алгебраических дополнений: все элементы присоединённой матрицы
   
   Cделим на определитель начальной матрицы. Итоговая матрица будет искомой обратной матрицей относительно заданной.
5. Проверяем выполненную работу: умножаем матрицу начальную и полученную матрицы, результатом должна стать единичная матрица.

Интересные факты

1. Матрицы были впервые введены в математику английским математиком Джеймсом Джозефом Сильвестром в 1850 году. Он назвал их “матрицами”, потому что они были похожи на таблицы, которые использовались в то время для записи данных.

2. Матрицы используются во многих областях математики, физики, инженерии и других наук. Они используются для решения систем линейных уравнений, для представления геометрических преобразований, для анализа данных и для многих других целей.

3. Матрицы также используются в компьютерной графике для представления трехмерных объектов. Каждая точка в трехмерном пространстве может быть представлена в виде матрицы 4×4, которая содержит информацию о ее положении и ориентации.

Операции над матрицами #1

Решение систем матриц.

Для

решения систем матрицнаиболее часто используют метод Гаусса.

Метод Гаусса — это стандартный способ решения систем линейных алгебраических уравнений (СЛАУ) и он заключается в том, что последовательно исключаются переменные, т.е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы.

Метод Гауссаявляется самым универсальным и лучшим инструментом для нахождения решения матриц. Если у системы бесконечное множество решений или система является несовместимой, то ее нельзя решать по правилу Крамера и матричным методом.

Метод Гаусса подразумевает также прямой (приведение расширенной матрицы к ступенчатому виду, т.е. получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и есть метод Гаусса, обратный – метод Гаусса-Жордана. Метод Гаусса-Жордана отличается от метода Гаусса лишь последовательностью исключения переменных.

Матрицы в математике – один из важнейших объектов, имеющих прикладное значение. Часто
экскурс в теорию матриц начинают со слов: “Матрица – это прямоугольная таблица…”. Мы начнём этот экскурс
несколько с другой стороны.

Телефонные книги любого размера и с любым числом данных об абоненте – ни что иное, как матрицы. Такие матрицы
имеют примерно следующий вид:

Ясно, что такими матрицами мы все пользуемся почти каждый день. Эти матрицы бывают с различным
числом строк (различаются как выпущенный телефонной компанией справочник, в котором могут быть тысячи, сотни тысяч и даже миллионы строк
и только что начатая Вами новая записная книжка, в которой меньше десяти строк) и столбцов (справочник должностных лиц какой-нибудь
организации, в котором могут быть такие столбцы, как должность и номер кабинета и та же Ваша записная книжка, где
может не быть никаких данных, кроме имени, и, таким образом, в ней только два столбца – имя и телефон).

Всякие матрицы можно складывать и умножать, а также проводить над ними другие операции,
однако нет необходимости складывать и умножать телефонные справочники, от этого нет никакой пользы, к тому
же можно и подвинуться рассудком.

Но очень многие матрицы можно и нужно складывать и перемножать и решать таким образом
различные насущные задачи. Ниже примеры таких матриц.

Матрицы, в которых столбцы – выпуск единиц продукции того или иного вида, а строки
– годы, в которых ведётся учёт выпуска этой продукции:

Можно складывать матрицы такого вида, в которых учтён выпуск аналогичной продукции
различными предприятиями, чтобы получить суммарные данные по отрасли.

Или матрицы, состоящие, к примеру, из одного столбца, в которых строки –
средняя себестоимость того или иного вида продукции:

Матрицы двух последних видов можно умножать, а в результате получится матрица-строка,
содержащая себестоимость всех видов продукции по годам.

Опыт других людей

Действия с матрицами вызывают разные отзывы у людей. Одни считают их сложными и непонятными, другие находят в них увлекательное занятие. Матрицы используются в различных областях, от физики и математики до компьютерных наук и экономики. Некоторые отмечают, что работа с матрицами помогает им лучше понимать структуру данных и решать сложные задачи. В то же время, другие выражают затруднения при применении матриц в практических задачах. В целом, мнения о действиях с матрицами разнообразны, и каждый находит в них что-то своё.

МАТРИЦЫ и операции над ними

Матрицы, основные определения

Прямоугольная таблица, состоящая из чисел, расположенных в

mстроках и

nстолбцах, называется


mn-матрицей
(или просто


матрицей
) и записывается так:

(1)

В матрице (1) числа
называются её


элементами
(как и в определителе, первый индекс означает номер строки, второй – столбца, на пересечении которых стоит элемент;

i= 1, 2, …,

m;

j= 1, 2,

n).

Матрица называется


прямоугольной
, если
.

Если же

m=

n, то матрица называется


квадратной
, а число n – её


порядком
.

Определителем квадратной матрицы A
называется определитель, элементами которого являются элементы матрицы

A. Он обозначается символом |

A|.

Квадратная матрица называется


неособенной
(или


невырожденной
,


несингулярной
), если её определитель не равен нулю, и


особенной
(или


вырожденной
,


сингулярной
), если её определитель равен нулю.

Матрицы называются


равными
, если у них одинаковое число строк и столбцов и все соответствующие элементы совпадают.

Матрица называется


нулевой
, если всё её элементы равны нулю. Нулевую матрицу будем обозначать символом

0или
.

Например,

Матрицей-строкой
(или


строчной
) называется 1

n-матрица, а


матрицей-столбцом
(или


столбцовой
) –

m1-матрица.

Матрица

A”
, которая получается из матрицы

Aзаменой в ней местами строк и столбцов, называется


транспонированной
относительно матрицы

A. Таким образом, для матрицы (1) транспонированной является матрица

Операция перехода к матрице

A”
,
транспонированной относительно матрицы

A, называется транспонированием матрицы

A.
Для

mn-матрицы транспонированной является

nm-матрица.

Транспонированной относительно матрицы
является матрица

A, то есть

(

A“)” =

A.

Пример 1.Найти матрицу

A”
,
транспонированную относительно матрицы

и выяснить, равны ли определители исходной и транспонированной матриц.

Главной диагональю
квадратной матрицы называется воображаемая линия, соединяющая её элементы, у которых оба индекса одинаковые. Эти элементы называются


диагональными
.

Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется


диагональной
. Не обязательно все диагональные элементы диагональной матрицы отличны от нуля. Среди них могут быть и равные нулю.

Квадратная матрица, у которой элементы, стоящие на главной диагонали равны одному и тому же числу, отличному от нуля, а
все прочие равны нулю, называется


скалярной матрицей
.

Единичной матрицей
называется диагональная матрица, у которой все диагональные элементы равны единице. Например, единичной матрицей третьего порядка является матрица

Пример 2.Даны матрицы:

Решение. Вычислим определители данных матриц. Пользуясь правилом треугольников, найдём

Определитель матрицы

Bвычислим по формуле

Легко получаем, что

Следовательно, матрицы

Aи
– неособенные (невырожденные, несингулярные), а матрица

B– особенная (вырожденная, сингулярная).

Определитель единичной матрицы любого порядка, очевидно, равен единице.

Решить задачу на матрицы самостоятельно, а затем посмотреть решение

Пример 3.Даны матрицы

,

,

Установить, какие из них являются неособенными (невырожденными, несингулярными).

Применение матриц в математико-экономическом моделировании

В виде матриц просто и удобно записываются структурированные данные о том или ином объекте. Матричные
модели создаются не только для хранения этих структурированных данных, но и для решения различных задач с этими данными
средствами линейной алгебры.

Так, известной матричной моделью экономики является модель “затраты-выпуск”, внедрённая американским
экономистом русского происхождения Василием Леонтьевым. Эта модель исходит из предположения, что весь производственный
сектор экономики разбит на

nчистых отраслей. Каждая из отраслей выпускает продукцию только одного вида и разные отрасли
выпускают разную продукцию. Из-за такого разделения труда между отраслями существуют межотраслевые связи, смысл которых
состоит в том, что часть продукции каждой отрасли передаётся другим отраслям в качестве ресурса производства.

Объём продукции

i-й отрасли (измеряемый определённой единицей измерения), которая была произведена
за отчётный период, обозначается через и
называется полным выпуском

i-й отрасли. Выпуски
удобно разместить в

n-компонентную строку матрицы.

Количество единиц продукции

i-й отрасли, которое необходимо затратить

j-й
отрасли для производства единицы своей продукции, обозначается
и называется коэффициентом прямых затрат.

Определение
1.

Матрицей
А размера
m

nназывается прямоугольная таблица из m
строк и n
столбцов, состоящая из чисел или иных
математических выражений
(называемых элементами матрицы),i
= 1,2,3,…,m,
j
= 1,2,3,…,n.

,
или

Определение
2.
Две матрицы

и

одного размера называются

равными,
если они совпадают поэлементно, т.е.
=
,i
= 1,2,3,…,m,
j
= 1,2,3,…,n.

С
помощью матриц легко записывать некоторые
экономические зависимости, например
таблицы распределения ресурсов по
некоторым отраслям экономики.

Определение
3.
Если число строк матрицы совпадает с
числом ее столбцов, т.е. m
= n,
то матрица называется

квадратной
порядка
n
,а в противном случае

прямоугольной.

Определение
4.
Переход от матрицы А к матрице А т, в которой строки и столбцы поменялись
местами с сохранением порядка, называется

транспонированиемматрицы.

Виды
матриц: квадратная (размера 33)
–

,

прямоугольная
(размера 25)
–

,

диагональная
–

,
единичная –

,
нулевая –

,

матрица-строка
–

,
матрица-столбец -.

Определение
5.

Элементы
квадратной матрицы порядка n
с одинаковыми индексами называются
элементами главной диагонали, т.е. это
элементы:

.

Определение
6.

Элементы
квадратной матрицы порядка n
называются элементами побочной диагонали,
если сумма их индексов равна n
+ 1, т.е. это элементы:
.

1.2. Операции над матрицами.

1
0
.

Суммой
двух матриц

и

одинакового размера называется матрица
С = (с ij),
элементы которой определяются равенством
с ij
= a ij
+ b ij ,
(i
= 1,2,3,…,m,
j
= 1,2,3,…,n).

Свойства
операции сложения матриц.

Для
любых матриц А,В,С одного размера
выполняются равенства:

1)
А + В = В + А (коммутативность),

2)
(А + В) + С = А + (В + С) = А + В + С (ассоциативность).

2
0
.

Произведением


матрицы



на число



называется матрица

того же размера, что и матрица А, причемb ij
= 
(i
= 1,2,3,…,m,
j
= 1,2,3,…,n).

Свойства
операции умножения матрицы на число.

(А)
= ()А
(ассоциативность
умножения);

(А+В)
= А+В
(дистрибутивность умножения относительно
сложения матриц);

(+)А
= А+А
(дистрибутивность умножения относительно
сложения чисел).

Определение 7.
Линейной
комбинацией матриц

и

одинакового размера называется выражение
видаА+В,
где 
и 
– произвольные числа.

3
0
.

Произведением
А





В
матриц
А
и В соответственно
размеров mn
и nk
называется матрица С размера mk,
такая, что элемент с ij
равен сумме произведений элементов
i-той
строки матрицы А и j-того
столбца матрицы В, т.е. с ij
= a i 1 b 1 j +a i 2 b 2 j +…+a ik b kj .

Произведение
АВ существует, только в том случае, если
число столбцов матрицы А совпадает с
числом строк матрицы В.

Свойства операции умножения матриц:

(АВ)С
= А(ВС)
(ассоциативность);

(А+В)С
= АС+ВС
(дистрибутивность относительно
сложения матриц);

А(В+С)
= АВ+АС
(дистрибутивность относительно
сложения матриц);

АВ

ВА
(не коммутативность).

Определение 8.

Матрицы
А и В, для которых АВ = ВА, называются
коммутирующими или перестановочными.

Умножение
квадратной матрицы любого порядка на
соответствующую единичную матрицу не
меняет матрицу.

Определение 9.

Элементарными
преобразованиямиматриц называются следующие операции:

Перемена
местами двух строк (столбцов).

Умножение
каждого элемента строки (столбца) на
число, отличное от нуля.

Прибавление
к элементам одной строки (столбца)
соответствующих элементов другой
строки (столбца).

Определение 10.

Матрица
В, полученная из матрицы А с помощью
элементарных преобразований называется

эквивалентной(обозначается ВА).

Пример
1.1.Найти линейную комбинацию матриц 2А–3В,
если

,

.

,

,

.

Пример

1.2.Найти
произведение матриц

,
если

.

Решение:
т.к количество столбцов первой матрицы
совпадает с количеством строк второй
матрицы, то произведение матриц
существует. В результате получаем новую
матрицу

,
где

В
результате получим

.

Лекция
2. Определители. Вычисление определителей
второго, третьего порядка. Свойства
определителей
n
-го
порядка.

Матрицей называется прямоугольная таблица из чисел с некоторым количеством

mстрок и с некоторым количеством

nстолбцов. Числа

mи

nназываются

порядкамиили

размерамиматрицы.

Матрица порядка

m × nзаписывается в форме:

или

(i=

1,2,…m; j=

1,2,…n).

Числа

a ijвходящие в состав данной матрицы называются ее элементами. В записи

a ijпервый индекс

iозначает номер строки, а второй индекс

j– номер столбца.

Матрица строка

Матрица размером 1

×n, т.е. состоящая из одной строки, называется

матрицей-строкой. Например:

Матрица столбец

Матрица размером

m×1, т.е. состоящая из одного столбца, называется

матрицей-столбцом. Например

Нулевая матрица

Если все элементы матрицы равны нулю,то матрица называется

нулевой матрицей. Например

Квадратная матрица

Матрица

Aпорядка

m×nназывается

квадратной матрицей, если количество строк и столбцов совпадают:

m=n. Число

m=nназывается

порядкомквадратной матрицы. Например:

Главная диагональ матрицы

a 11 , a 22 ,…, a nnобразуют

главную диагональматрицы. Например:

В случае

m×n-матриц элементы

a ii (i=

1,2,…,min(m,n))также образуют

главную диагональ. Например:

Элементы расположенные на главной диагонали называются

главными диагональными элементамиили просто

диагональными элементами.

Побочная диагональ матрицы

Элементы расположенные на местах

a 1n , a 2n-1 ,…, a n1образуют

побочную диагональматрицы. Например:

Диагональная матрица

Квадратная матрица называется

диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

Единичная матрица

Квадратную матрицу

n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется

единичной матрицейи обозначается через

Eили

En , где

n– порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:

След матрицы

Сумма главных диагональных элементов матрицы

Aназывается

следомматрицы и обозначается Sp

Aили Tr

A. Например:

Верхняя треугольная матрица

Квадратная матрица порядка n×n называется

верхней треугольнойматрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е.

a ij =0, при всех

i>j. Например:

Нижняя треугольная матрица

Квадратная матрица порядка

n×nназывается

нижней треугольнойматрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е.

a ij =0, при всех

i

. Например:

Cтроки матрицы

Aобразуют

пространство строк
R(AT).

Cтолбцы матрицы

Aобразуют

пространство столбцовматрицы и обозначаются через

R(A).

Ядро или нуль пространство матрицы

Множесто всех решений уравнения

Ax=0, где

A- mx

n-матрица,

x– вектор длины

n– образует

нуль пространствоили

ядроматрицы

Aи обозначается через

Ker(A)или

N(A).

Противоположная матрица

Для любой матрицы

Aсущеcтвует противоположная матрица

-Aтакая, что

A+(-A)=0.Очевидно, что в качестве матрицы

-Aследует взять матрицу

(-1)A, элементы которой отличаются от элементов

Aзнаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Разность матриц

Разностью

Cдвух матриц

Aи

Bодинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера

n×n.Тогда степень матрицы определяется следующим образом:

где E-единичная матрица.

Из сочетательного свойства умножения следует:

где

p,q– произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию

A=A Tназывается симметричной матрицей.

Для симметричных матриц имеет место равенство:

a ij =a ji ; i=1,2,…n, j=1,2,…n

Линейная алгебра

Матрицы

Матрицаразмера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы принято обозначать заглавными латинскими буквами, а элементы – теми же, но строчными буквами с двойной индексацией.

Например, рассмотрим матрицу А размерности 2 х 3:

В этой матрице две строки (m = 2) и три столбца (n = 3), т.е. она состоит из шести элементов a ij , где i – номер строки, j – номер столбца. При этом принимает значения от 1 до 2, а от одного до трех (записывается ). А именно, a 11 = 3; a 12 = 0; a 13 = -1; a 21 = 0; a 22 = 1,5; a 23 = 5.

Матрицы А и В одного размера (m х n) называют

равными, если они поэлементно совпадают, т.е. a ij = b ij для , т.е. для любых i и j (можно записать “i, j).

Матрица-строка– это матрица, состоящая из одной строки, а

матрица-столбец– это матрица, состоящая из одного столбца.

Например,
– матрица-строка, а .

Квадратная матрицаn-го порядка – это матрица, в число строк равно числу столбцов и равно n.

Например, – квадратная матрица второго порядка.

Диагональныеэлементы матрицы – это элементы, у которых номер строки равен номеру столбца (a ij , i = j). Эти элементы образуют

главную диагональматрицы. В предыдущем примере главную диагональ образуют элементы a 11 = 3 и a 22 = 5.

Диагональная матрица– это квадратная матрица, в которой все недиагональные элементы равны нулю. Например,
– диагональная матрица третьего порядка. Если при этом все диагональные элементы равны единице, то матрица называется

единичной(обычно обозначаются буквой Е). Например,
– единичная матрица третьего порядка.

Матрица называется

нулевой, если все ее элементы равны нулю.

Квадратная матрица называется

треугольной, если все ее элементы ниже (или выше) главной диагонали равны нулю. Например,
– треугольная матрица третьего порядка.

Операции над матрицами

Над матрицами можно производить следующие операции:

1.

Умножение матрицы на число. Произведением матрицы А на число l называется матрица В = lА, элементы которой b ij = la ij для любых i и j.

Например, если , то
.

2.

Сложение матриц. Суммой двух матриц А и В одинакового размера m х n называется матрица С = А + В, элементы которой с ij = a ij + b ij для “i, j.

Например, если
то

.

Отметим, что через предыдущие операции можно определить

вычитание матрицодинакового размера: разность А-В = А + (-1)*В.

3.

Умножение матриц. Произведением матрицы А размера m x n на матрицу В размера n x p называется такая матрица С, каждый элемент которой с ij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В, т.е.
.

Например, если

, то размер матрицы-произведения будет 2 x 3, и она будет иметь вид:

В этом случае матрица А называется согласованной с матрицей В.

На основе операции умножения для квадратных матриц определена операция

возведения в степень. Целой положительной степенью А m (m > 1) квадратной матрицы А называются произведение m матриц, равных А, т.е.

Подчеркнем, что сложение (вычитание) и умножение матриц определены не для любых двух матриц, а только для удовлетворяющим определенным требованиям к своей размерности. Для нахождения суммы или разности матриц их размер обязательно должен быть одинаковым. Для нахождения произведения матриц число столбцов первой из них должно совпадать с числом строк второй (такие матрицы называют

согласованными).

Рассмотрим некоторые свойства рассмотренных операций, аналогичные свойствам операций над числами.

1) Коммутативный (переместительный) закон сложения:

А + В = В + А

2) Ассоциативный (сочетательный) закон сложения:

(А + В) + С = А + (В + С)

3) Дистрибутивный (распределительный) закон умножения относительно сложения:

l(А + В) = lА + lВ

А (В + С) = АВ + АС

(А + В) С = АС + ВС

5) Ассоциативный (сочетательный) закон умножения:

l(АВ) = (lА)В = А(lВ)

A(BС) = (АВ)С

Подчеркнем, что переместительный закон умножения для матриц в общем случае НЕ выполняется, т.е. AB ¹ BA. Более того, из существования AB не обязательно следует существование ВА (матрицы могут быть не согласованными, и тогда их произведение вообще не определено, как в приведенном примере умножения матриц). Но даже если оба произведения существуют, они обычно разные.

В частном случае коммутативным законом обладает произведение любой квадратной матрицы А на единичную матрицу того же порядка, причем это произведение равно А (умножение на единичную матрицу здесь аналогично умножению на единицу при умножении чисел):

АЕ = ЕА = А

В самом деле,

Подчеркнем еще одно отличие умножения матриц от умножения чисел. Произведение чисел может равняться нулю тогда и только тогда, когда хотя бы одно из них равно нулю. О матрицах этого сказать нельзя, т.е. произведение ненулевых матриц может равняться нулевой матрице. Например,

Продолжим рассмотрение операций над матрицами.

4.

Транспонирование матрицыпредставляет собой операцию перехода от матрицы А размера m x n к матрице А Т размера n x m, в которой строки и столбцы поменялись местами:

%.

Свойства операции транспонирования:

1) Из определения следует, что если матрицу транспонировать дважды, мы вернемся к исходной матрице: (A T) T = A.

2) Постоянный множитель можно вынести за знак транспонирования: (lА) T = lА T .

3) Транспонирование дистрибутивно относительно умножения и сложения матриц: (AB) T = B T A T и (A + B) T = B T + A T .

Определители матриц

Для каждой квадратной матрицы А вводится число |А|, которое называют ее

определителем. Иногда его еще обозначают буквой D.

Это понятие является важным для решения ряда практических задач. Определим его через способ вычисления.

Для матрицы А первого порядка ее определителем называют ее единственный элемент |А| = D 1 = а 11 .

Для матрицы А второго порядка ее определителем называют число, которое вычисляют по формуле |А| = D 2 = а 11 * а 22 – а 21 * а 12

Для матрицы А третьего порядка ее определителем называют число, которое вычисляют по формуле

Оно представляет алгебраическую сумму, состоящую из 6 слагаемых, в каждое из которых входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Для запоминания формулы определителя принято пользоваться так называемым правилом треугольников или правилом Сарруса (рисунок 6.1).

На рисунке 6.1 схема слева показывает, каким образом выбирать элементы для слагаемых со знаком «плюс», – они находятся на главной диагонали и в вершинах равнобедренных треугольников, основания которых ей параллельны. Схема слева используется для слагаемых со знаком «минус»; на ней вместо главной диагонали берется так называемая побочная.

Определители более высоких порядков вычисляют рекуррентным способом, т.е. определитель четвертого порядка через определитель третьего порядка, определитель пятого порядка через определитель четвертого порядка и т.д. Для описания этого способа необходимо ввести понятия минора и алгебраического дополнения элемента матрицы (сразу же отметим, что сам способ, который будет рассмотрен далее, подходит и для определителей третьего и второго порядка).

МиноромМ ij элемента а ij матрицы n-го порядка называют определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца.

Каждая матрица n-го порядка имеет n 2 миноров (n-1)-го порядка.

Алгебраическим дополнениемA ij элемента а ij матрицы n-го порядка называют его минор, взятый со знаком (-1) (i+ j) :

A ij = (-1) (i+ j) *М ij

Из определения следует, что A ij = М ij , если сумма номеров строки и столбца четная, и A ij = -М ij , если она нечетная.

Например, если
, то
;
и т.д.

Способ вычисления определителясостоит в следующем: определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

(разложение по элементам i-й строки; );

(разложение по элементам j-го столбца; ).

Например,

Отметим, что и в общем случае определитель треугольной матрицы равен произведению элементов главной диагонали.

Сформулируем основные свойства определителей.

1. Если какая-либо строка или столбец матрицы состоит из одних нулей, то определитель равен 0 (следует из способа расчета).

2. Если все элементы какой-либо строки (столбца) матрицы умножить на одно и то же число, то и ее определитель умножится на это число (также следует из способа расчета – на расчет алгебраических дополнений общий множитель не влияет, а все остальные слагаемые умножены именно на это число).

Замечание: за знак определителя можно выносить общий множитель именно строки или столбца (в отличие от матрицы, за знак которой можно выносить общий множитель всех ее элементов). Например, , но
.

3. При транспонировании матрицы ее определитель не изменяется: |А Т | = |А| (доказательство проводить не будем).

4. При перестановке местами двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

Для доказательства этого свойства вначале предположим, что переставлены две соседние строки матрицы: i-я и (i+1)-я. Для расчета определителя исходной матрицы осуществим разложение по i-й строке, а для определителя новой матрицы (с переставленными строками) – по (i+1)–й (которая в ней такая же, т.е. поэлементно совпадает). Тогда при расчете второго определителя каждое алгебраическое дополнение будет иметь противоположный знак, так как (-1) будет возводиться не в степень (i + j), а в степень (i + 1+ j), а в остальном формулы отличаться не будут. Таким образом, знак определителя изменится на противоположный.

Теперь предположим, что переставлены не соседние, а две произвольные строки, например, i-я и (i+t)-я. Такую перестановку можно представить как последовательное смещение i-й строки на t строк вниз, а (i+t)-й строки – на (t-1) строк вверх. При этом знак определителя поменяется (t + t – 1) = 2t – 1 число раз, т.е. нечетное число раз. Следовательно, в конечном итоге он поменяется на противоположный.

Аналогичные рассуждения можно поменять для столбцов.

5. Если матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.

В самом деле, если одинаковые строки (столбцы) переставить местами, то будет получена та же самая матрица с тем же самым определителей. С другой стороны, по предыдущему свойству он должен поменять знак, т.е. D = -D Û D = 0.

6. Если элементы двух строк (столбцов) матрицы пропорциональны, то определитель равен 0.

Это свойство основано на предыдущем свойстве и выносе за скобку общего множителя (после выноса за скобку коэффициента пропорциональности в матрице будут одинаковые строки или столбцы, и в результате этот коэффициент будет умножаться на ноль).

7. Сумма произведений элементов любой строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) той же матрицы всегда равна 0:
при i ¹ j.

Чтобы доказать это свойство, достаточно заменить в матрице А j–ю строку на i–ю. В полученной матрице будет две одинаковые строки, поэтому ее определитель равен 0. С другой стороны, его можно вычислить разложением по элементам j -й строки:
.

8. Определитель матрицы не изменяется, если к элементам строки или столбца матрицы прибавить элементы другой строки (столбца), умноженные на одно и тоже число.

В самом деле, пусть к элементам i–й строки прибавляют элементы j-й строки, умноженные на l. Тогда элементы новой i–й строки примут вид

(a ik + la jk , “k). Вычислим определитель новой матрицы разложением по элементам i-й строке (отметим, что алгебраические дополнения ее элементов при этом не изменятся):

Мы получили, что этот определитель не отличается от определителя исходной матрицы.

9. Определитель произведения матриц равен произведению их определителей: |АВ| = |А| * |В| (доказательство проводить не будем).

Рассмотренные выше свойства определителей используют для упрощения их вычисления. Обычно стараются преобразовать матрицу к такому виду, чтобы какой-либо столбец или строка содержали как можно больше нулей. После этого определитель легко найти разложением по этой строке или столбцу.

Обратная матрица

Матрицу А -1 называют

обратнойпо отношению к квадратной матрице А, если при умножении этой матрицы на матрицу А как справа, так и слева получается единичная матрица: А -1 * А = А * А -1 = Е.

Из определения следует, что обратная матрица является квадратной матрицей того же порядка, что и матрица А.

Можно отметить, что понятие обратной матрицы аналогично понятию обратного числа (это число, которое при умножении на данное число дает единицу: а*а -1 = а*(1/а) = 1).

Все числа, кроме нуля, имеют обратные числа.

Чтобы решить вопрос о том, имеет ли квадратная матрица обратную, необходимо найти ее определитель. Если определитель матрицы равен нулю, то такая матрица называется

вырожденной, или

особенной.

Необходимое и достаточное условие существования обратной матрицы: обратная матрица существует и единственна тогда и только тогда, когда исходная матрица невырожденная.

Докажем необходимость. Пусть матрица А имеет обратную матрицу А -1 , т.е. А -1 * А = Е. Тогда |А -1 * А| = |А -1 | * |А| = |Е| = 1. Следовательно,

|А| ¹ 0.

Докажем достаточность. Чтобы его доказать, необходимо просто описать способ вычисления обратной матрицы, который мы всегда сможем применить для невырожденной матрицы.

Итак, пусть |А| ¹ 0. Транспонируем матрицу А. Для каждого элемента А Т найдем алгебраическое дополнение и составим из них матрицу , которую называют

присоединенной(взаимной, союзной): .

Найдем произведение присоединенной матрицы и исходной . Получим
. Таким образом матрица В – диагональная. На ее главной диагонали стоят определители исходной матрицы, а все остальные элементы – нули:

Аналогично можно показать, что .

Если разделить все элементы матрицы на |А|, то будет получена единичная матрица Е.

Таким образом
, т.е. .

Докажем единственность обратной матрицы. Предположим, что существует другая обратная матрица для А, отличная от А -1 . Обозначим ее X. Тогда А * Х = Е. Умножим слева обе части равенства на А -1 .

А -1 * А * Х = А -1 * Е

Единственность доказана.

Итак, алгоритм вычисления обратной матрицы состоит из следующих шагов:

1. Найти определитель матрицы |А| . Если |А| = 0, то матрица А – вырожденная, и обратную матрицу найти нельзя. Если |А| ¹ 0, то переходят к следующему шагу.

2. Построить транспонированную матрицу А Т.

3. Найти алгебраические дополнения элементов транспонированной матрицы и построить присоединенную матрицу .

4. Вычислить обратную матрицу, разделив присоединенную матрицу на |А|.

5. Можно проверить правильность вычисления обратной матрицы в соответствии с определением: А -1 * А = А * А -1 = Е.

1. Найдем определитель этой матрицы по правилу треугольников:

Проверку опустим.

Можно доказать следующие свойства обращения матриц:

1) |А -1 | = 1/|А|

2) (А -1) -1 = А

3) (А m) -1 = (А -1) m

4) (АB) -1 = B -1 * А -1

5) (А -1) T = (А T) -1

Ранг матрицы

Минором k-го порядкаматрицы А размера m х n называют определитель квадратной матрицы k-го порядка, которая получена из матрицы А вычеркиванием каких-либо строк и столбцов.

Из определения следует, что порядок минора не превосходит меньшего из ее размеров, т.е. k £ min {m; n}. Например, из матрицы А 5х3 можно получить квадратные подматрицы первого, второго и третьего порядков (соответственно, рассчитать миноры этих порядков).

Рангомматрицы называют наивысший порядок отличных от нуля миноров этой матрицы (обозначают rang А, или r(А)).

Из определения следует, что

1) ранг матрицы не превосходит меньшего из ее размеров, т.е.

r(А) £ min {m; n};

2) r(А) = 0 тогда и только тогда, когда матрица нулевая (все элементы матрицы равны нулю), т.е. r(А) = 0 Û А = 0;

3) для квадратной матрицы n-го порядка r(А) = n тогда и только тогда, когда эта матрица А невырожденная, т.е. r(А) = n Û |А| ¹ 0.

На самом деле, для этого достаточно вычислить только один такой минор (тот, который получен вычеркиванием третьего столбца (потому что в остальных будет присутствовать нулевой третий столбец, и поэтому они равны нулю).

По правилу треугольника
= 1*2*(-3) + 3*1*2 + 3*(-1)*4 – 4*2*2 – 1*(-1)*1 – 3*3*(-3) = -6 +6 – 12 – 16 + 1 +27 = 0.

Поскольку все миноры третьего порядка нулевые, r(А) £ 2. Так как существует ненулевой минор второго порядка, например,

Очевидно, что использованные нами приемы (рассмотрение всевозможных миноров) не подходят для определения ранга в более сложных случаях ввиду большой трудоемкости. Обычно для нахождения ранга матрицы используют некоторые преобразования, которые называют

элементарными:

1). Отбрасывание нулевых строк (столбцов).

2). Умножение всех элементов строки или столбца матрицы на число, отличное от нуля.

3). Изменение порядка строк (столбцов) матрицы.

4). Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5). Транспонирование.

Если матрица А получена из матрицы B элементарными преобразованиями, то эти матрицы называют

эквивалентнымии обозначают А ~ В.

Теорема. Элементарные преобразования матрицы не изменяют ее ранг.

Доказательство теоремы следует из свойств определителя матрицы. В самом деле, при этих преобразованиях определители квадратных матриц либо сохраняются, либо умножаются на число, не равное нулю. В результате наивысший порядок отличных от нуля миноров исходной матрицы остается прежним, т.е. ее ранг не меняются.

С помощью элементарных преобразований матрицу приводят к так называемому ступенчатому виду (преобразуют в

ступенчатую матрицу), т.е. добиваются, чтобы в эквивалентной матрице под главной диагональю стояли только нулевые элементы, а на главной диагонали – ненулевые:

Ранг ступенчатой матрицы равен r, так как вычеркиванием из нее столбцов, начиная с (r + 1)-го и дальше можно получить треугольную матрицу r-го порядка, определитель которой будет отличен от нуля, так как будет представлять собой произведение ненулевых элементов (следовательно, имеется минор r-го порядка, не равный нулю):

Пример. Найти ранг матрицы

1). Если а 11 = 0 (как в нашем случае), то перестановкой строк или столбцов добьемся того, чтобы а 11 ¹ 0. Здесь поменяем местами 1-ю и 2-ю строки матрицы:

2). Теперь а 11 ¹ 0. Элементарными преобразованиями добьемся того, чтобы все остальные элементы в первом столбце равнялись нулю. Во второй строке a 21 = 0. В третьей строке a 31 = -4. Чтобы вместо (-4) стоял 0, прибавим к третьей строке первую строку, умноженную на 2 (т.е. на (-а 31 /а 11) = -(-4)/2 =

= 2). Аналогично к четвертой строке прибавим первую строку (умноженную на единицу, т.е. на (-а 41 /а 11) = -(-2)/2 = 1).

3). В полученной матрице а 22 ¹ 0 (если бы было а 22 = 0, то можно было бы снова переставить строки). Добьемся, чтобы ниже диагонали во втором столбце тоже стояли нули. Для этого к 3-й и 4-й строкам прибавим вторую строку, умноженную на -3 ((-а 32 /а 22) = (-а 42 /а 22) = -(-3)/(-1) = -3):

4). В полученной матрице две последние строки – нулевые, и их можно отбросить:

Получена ступенчатая матрица, состоящая из двух строк. Следовательно, r(A) = 2.

Возможно, будет полезно почитать:

• Заявление о приостановке работы в связи с невыплатой зарплаты
  ;
• Что сказано об увольнении по собственному желанию в п
  ;
• Как восстановить утерянную квитанцию Потерял чек сбербанка можно ли восстановить
  ;
• Где взять номер лицевого счета для заявления на налоговый вычет?
  ;
• Порядок заполнения перечня заявлений о ввозе товаров и уплате косвенных налогов Проверить уплату косвенных налогов в белоруссии
  ;
• Поиск инн организации по названию
  ;
• Дистанционное обучение на бухгалтерских курсах
  ;
• Измерение величин Измеряется s в физике
  ;

Частые вопросы

Какие действия можно выполнять с матрицей?

Основные операции, которые можно выполнять с матрицами, включают сложение, вычитание и умножение. Сложение матриц выполняется путем поэлементного сложения соответствующих элементов матриц. Вычитание матриц выполняется аналогично — путем поэлементного вычитания.

Что значит что мы живем в матрице?

simulation hypothesis) — философская гипотеза о том, что окружающая нас реальность является симуляцией (чаще всего предполагается, что это компьютерная симуляция).

Что такое матрицы и действия над ними?

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), который представляет собой совокупность строк и столбцов, на пересечении которых находятся его элементы. Количество строк и столбцов задает размер матрицы.

Где используются матрицы в жизни?

Математические матрицы широко применяются в различных областях, таких как физика, экономика, компьютерная графика, машинное обучение и др. Они позволяют компактно представлять и обрабатывать данные, решать системы линейных уравнений, выполнять преобразования координат и многое другое.

Полезные советы

СОВЕТ №1

Изучите основные операции с матрицами, такие как сложение, вычитание, умножение на число и умножение матриц.

СОВЕТ №2

Познакомьтесь с определителем матрицы и его свойствами, такими как вычисление определителя, обратимость матрицы и вычисление обратной матрицы.

СОВЕТ №3

Изучите применение матриц в решении систем линейных уравнений и в геометрии, таких как трансформации и преобразования координат.