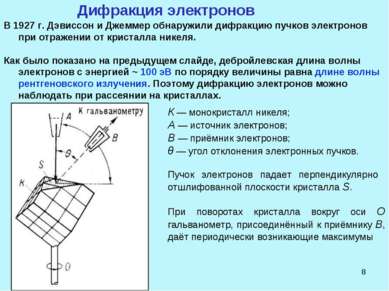
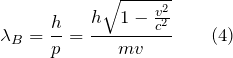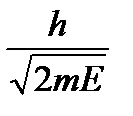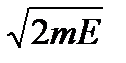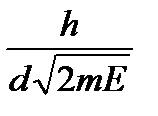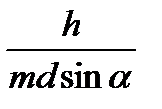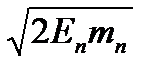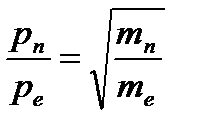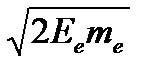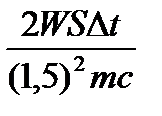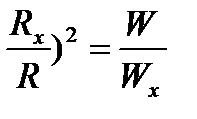Схема опыта Дэвиссона–Джермера (1927г.): К – монокристалл никеля; А – источник электронов; В – приёмник электронов; θ – угол отклонения электронных пучков.
Пучок электронов падает перпендикулярно отшлифованной плоскости кристалла S. При поворотах кристалла вокруг оси О гальванометр, присоединённый к приёмнику В, даёт периодически возникающие максимумы
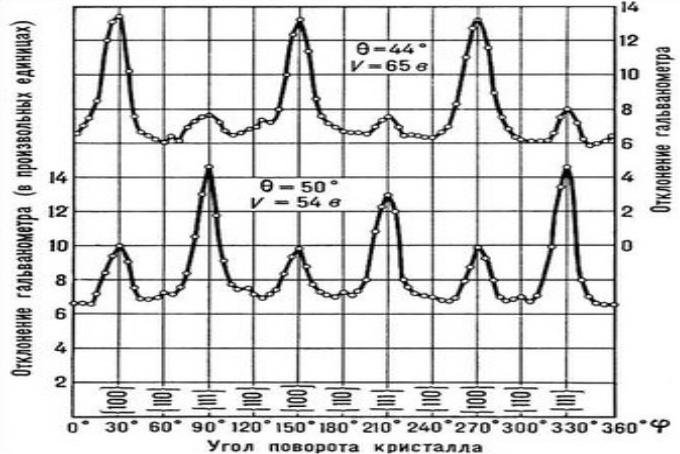
Запись дифракционных максимумов в опыте Дэвиссона–Джермера по дифракции электронов при различных углах поворота кристалла φ для двух значений угла отклонения электронов θ и двух ускоряющих напряжений V
. Максимумы отвечают отражению от различных кристаллографических плоскостей, индексы которых указаны в скобках
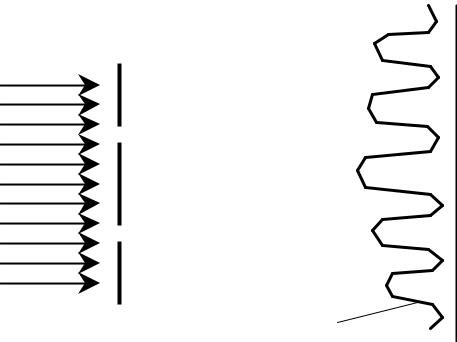
Эксперимент с двумя щелями в случае света и электронов
Свет или электроны
Распределение интенсивности на экране
Английский физик
Поль Андриен Морис Дирá к (Paul Adrien Maurice Dirac)
(8.08.1902-1984)
7.2.3. Принцип неопределённостинности
Гейзенберга
Квантовая механика (волновая механика) –
теория, устанавливающая способ описания и законы движения микрочастиц в заданных внешних полях.
Невозможно произвести измерение, не внося в измеряемый объект какое-нибудь возмущение, хотя бы слабое. Сам акт наблюдения вносит существенную неопределённость либо в положение, либо в импульс электрона. В этом и заключается
принцип неопределённости
,
впервые сформулированный Гейзенбергом в
Неравенства Гейзенберга
Dx
Dp
x
³ ,
Dy
Dp
y
³ ,
Dz
Dp
z
³
Dt
× D(E′
— E
)
³
7.2.4.
Волновые функции
ии
В
квантовой механике амплитуду, скажем, электронной волны называют
волновой функцией
и
обозначают греческой буквой «пси»: Ψ.
Таким образом, Ψ задаёт амплитуду нового типа поля, которое можно было бы назвать полем или волной материи, как функцию времени и положения.
Физический смысл функции Ψ заключается в том, что квадрат её модуля даёт плотность вероятности (вероятность, отнесённую к единице объёма) нахождения частицы в соответствующем месте пространства.
|
© А.В. Бармасов, 1998-2013 |
ОПРЕДЕЛЕНИЕ
Дифракцией электроновназывают процесс рассеяния данных элементарных частиц на системах частиц вещества. При этом электрон проявляет волновые свойства.
В первой половине XX века Л. де Бройль представил гипотезу о корпускулярно-волновом дуализме различных форма материи. Ученый полагал, электроны наряду с фотонами и другими частицами обладают и корпускулярными и волновыми свойствами. К корпускулярным характеристикам частицы можно отнести: ее энергию (E), импульс (), к волновым параметрам относят: частоту () и длину волны (). При этом волновые и корпускулярные параметры малых частиц связаны формулами:
где h — постоянная Планка.
Каждой частице массы в соответствии с идеей де Бройля, сопоставляется волна, имеющая длину :
Для релятивистского случая:
Дифракция электронов на кристаллах
Первым эмпирическим доказательством, которое подтверждало гипотезу де Бройля был эксперимент американских ученых К Девиссона и Л. Джермера. Они установили, что если пучок электронов рассеивать на кристалле никеля, то получается четкая картина дифракции, которая аналогична картине рассеивания на этом кристалле рентгеновского излучения. Атомные плоскости кристалла играли роль дифракционной решетки. Это стало возможным так как при разности потенциалов в 100 В длина волны Де Бройля для электрона равна приблизительно м, это расстояние сравнимо с расстояние между атомными плоскостями используемого кристалла.
Дифракция электронов на кристаллах аналогична дифракции лучей рентгена. Дифракционный максимум отраженной волны появляется при величинах угла Брэгга (), если он удовлетворяет условию:
где d — постоянная решетки кристалла (расстояние между плоскостями отражения); — порядок отражения. Выражение (4) означает то, что максимум дифракции возникает тогда, когда разность хода волн, отражающихся от соседних атомных плоскостей будет равна целому числу длин волн Де Бройля.
Г. Томсон наблюдал картину дифракции электронов на тонкой золотой фольге. На фотографической пластинке, которая находилась за фольгой, были получены концентрические светлые и темные кольца. Радиус колец зависели от скорости движения электронов, которая по Де Бройлю связана с длиной волны. Для установления природы дифрагировавших частиц в данном опыте в пространстве между фольгой и фотографической пластиной создавали магнитное поле. Магнитное поле должно искажать картину дифракции, если картину дифракции создают электроны. Так и случилось.
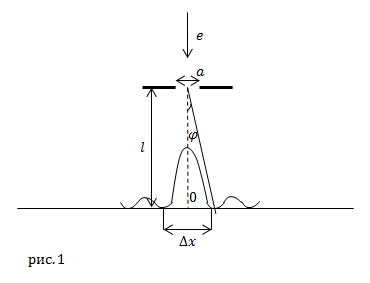
Дифракцию пучка моноэнергетических электронов на узкой щели, при нормальном падении пучка, можно характеризовать выражением (условие возникновения главных минимумов интенсивности):
где — угол между нормалью к решетке и направлением распространения дифрагированных лучей; a — ширина щели; k — порядок минимума дифракции; — длина волны де Бройля для электрона.
В середине XX века в СССР был проведен опыт по дифракции на тонкой пленке одиночных электронов, которые летели по очереди.
Так как дифракционные эффекты для электронов наблюдаются только если длина волны, связанная с элементарной частицей имеет такой же порядок как величина расстояния между атомами в веществе, то для изучения структуры вещества применяют метод электонографии, основанный на явлении дифракции электронов. Электронография используется для исследования структур поверхностей тел, так как проникающая способность электронов мала.
При помощи явления дифракции электронов находят расстояния между атомами в молекуле газов, которые адсорбируются на поверхности твердого тела.
Мнение эксперта:
Ученые создали «наклонный» пучок электронов, что открывает новые перспективы для изучения электромагнитного излучения. Эксперты отмечают, что данное достижение может привести к разработке более эффективных методов обнаружения и измерения электромагнитных полей. Кроме того, такие инновации могут найти применение в различных областях, включая медицинскую диагностику, связь и научные исследования. Это открытие подчеркивает важность фундаментальных исследований в области физики и технологий, и может стать отправной точкой для новых открытий и технологических разработок.

Опыт других людей
Электромагнитное излучение вызывает большой интерес у людей, и мнения по этому поводу различны. Одни считают его опасным для здоровья, другие утверждают, что оно несет большие преимущества для технологического прогресса. Недавно ученые создали «наклонный» пучок электронов, что вызвало новую волну обсуждений. Некоторые видят в этом потенциал для развития новых технологий, в то время как другие выражают опасения относительно возможных негативных последствий. Тем не менее, дальнейшие исследования и тщательное наблюдение помогут понять, какие перспективы открывает этот новый научный достижение.
Интересные факты
-
Ученые из Института физики плазмы Общества Макса Планка в Германии создали «наклонный» пучок электронов, который может использоваться для изучения фундаментальных свойств материи и для разработки новых технологий. Этот пучок электронов имеет уникальные свойства, которые позволяют ему проникать в материалы глубже, чем обычные пучки электронов, и взаимодействовать с ними более эффективно.
-
«Наклонный» пучок электронов создается с помощью специального устройства, которое называется «наклонный инжектор». Это устройство использует сильное магнитное поле для того, чтобы отклонить пучок электронов от его первоначального направления. В результате этого пучок электронов приобретает «наклонный» угол, который позволяет ему проникать в материалы глубже, чем обычные пучки электронов.
-
«Наклонный» пучок электронов может использоваться для изучения фундаментальных свойств материи, таких как структура атомов и молекул. Он также может использоваться для разработки новых технологий, таких как более эффективные солнечные батареи и более мощные лазеры.

Примеры решения задач
ПРИМЕР 1
| Задание | Пучок электронов, обладающих одинаковыми энергиями, падает на кристалл, имеющий период нм. Какова скорость электронов (v), если брэгговское отражение первого порядка появляется, если угол скольжения равен ? |
| Решение | За основу решения задачи примем условие возникновения максимума дифракции отраженной волны:
где по условию . Согласно гипотезе де Бройля длина волны электрона равна (для релятивистского случая): Подставим Из (1.3) выразим искомую скорость: где кг — масса электрона; Дж с — постоянная Планка. Проведем вычисления скорости электрона: |
| Ответ |
ПРИМЕР 2
| Задание | Какова скорость электронов в параллельном пучке, если они направлены перпендикулярно на узкую щель, ширина которой равна a? Расстояние от щели до экрана равно l, ширина центрального максимума дифракции . |
| Решение | Сделаем рисунок.
В качестве решения задачи используем условие возникновения главных минимумов интенсивности: |
Cлайд 1
* Лекция № 3 Принцип корпускулярно-волнового дуализма Л. де Бройля и его экспериментальное подтверждение Лекция для студентов ФНМ, 2013 год Интерференция атомов He в двухщелевом эксперименте Н.В.Никитин О.В.Фотина, П.Р.Шарапова
Cлайд 2
* Корпускулярно – волновой дуализм для излучения Частица света: фотон – в области
видимого света
(термин Гильберта Льюиса, 1926 г!!!) гамма-квант – в области жёсткого (высо- коэнергичного) рентгеновского диапазона. Вопрос: e- и p – частицы. Могут ли они в определённых условиях обладать волновыми свойствами?
Cлайд 3
* Фазовая и групповая скорости волн Волна: – фазовая скорость. – размерность скорости где λ – длина волны, T – период волны. Фазовая скорость, так как u – это не скорость передачи сигнала. Сигнал передаётся с квадратом амплитуды волнового пакета. Пусть: A(k) «пикует» при k=k0 Покажем, что пакет движется с – групповой скоростью волны: Тогда: То есть сигнал действительно передаётся с групповой скоростью vg.
Cлайд 4
* Принцип корпускулярно – волнового дуализма Луи де Бройля Луи де Бройль распространил принцип корпускулярно – волнового дуализма на вещество (частицы, имеющие ненулевую массу покоя). Гипотеза де Бройля: «… быть может, каждое движущееся тело сопровождается волной, и что не возможно разделить движение тела и распространение волны» Louis-Victor-Pierre-Raymond, de Broglie (1892 — 1987) L. de Broglie. Ondes et quanta // Comptes rendus de l»Académie des sciences. — 1923. — Vol. 177. — P. 507-510. Русский перевод: Л. де Бройль. Волны и кванты // УФН. — 1967. — Т. 93. — С. 178–180. Или Л. де Бройль, «Избранные
научные труды
», т.1, стр. 193-196, М. «Логос», 2010
Нобелевская премия
по физике (1929) за открытие волновой природы материи
Cлайд 5
* Математическая реализация гипотезы де Бройля Необходимо непротиворечивым образом каждой частице сопоставить колебатель-ный процесс. Природа этого колебательного процесса остается без ответа. Используется релятивистский подход. Колебательный процесс в К»: где u – фазовая скорость волны материи. Колебательный процесс в К («волновая» точка зрения): Но и — отвечают одному и тому же колебательному процессу: Колебательный процесс в К («корпускулярная» точка зрения):
Cлайд 6
* Математическая реализация гипотезы де Бройля: фазовая и групповая скорости. Эквивалентность колебательных процессов означает, что: Положим n=0. Кроме того, x=vt. Тогда фазовая скорость волн де Бройля есть: Групповая скорость: Таким образом: vg= v, то есть групповая скорость волн де Бройля в точности равна скорости частицы, с которой эта волна ассоциирована! Триумф теории!!!
Cлайд 7
* Длина волны де Бройля Импульс релятивисткой частицы Покажем, что с точки зрения волн де Бройля, его можно записать как Действительно: Это ещё одна математическая формулировка проявления дуализма волна — частица Длина волны де Бройля: Численные оценки: а) длина волны де Бройля теннисного мячика с m =50 г и v =10 m/c размеров мячика => для макроскопических предметов волновые свойства не проявляются. б) электрон, ускоренный до энергии Ee=100 эВ. Т.к. mec2≈0,51 МэВ, то можно пользоваться нерелятивистскими формулами: ─ сравнима с длинной волны рентгеновского излучения.
Cлайд 8
* Дифракция электронов В 1927 г. Дэвиссон и Джеммер обнаружили дифракцию пучков электронов при отражении от кристалла никеля. Как было показано на предыдущем слайде, дебройлевская длина волны электронов с энергией ~ 100 эВ по порядку величины равна длине волны рентгеновского излучения. Поэтому дифракцию электронов можно наблюдать при рассеянии на кристаллах. К — монокристалл никеля; А — источник электронов; В — приёмник электронов; θ — угол отклонения электронных пучков. Пучок электронов падает перпендикулярно отшлифованной плоскости кристалла S. При поворотах кристалла вокруг оси О гальванометр, присоединённый к приёмнику В, даёт периодически возникающие максимумы
Cлайд 9
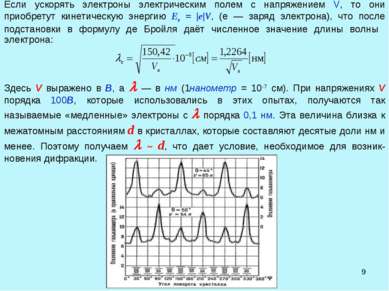
* Если ускорять электроны
электрическим полем
с напряжением V, то они приобретут кинетическую энергию Ee = |e|V, (е — заряд электрона), что после подстановки в формулу де Бройля даёт численное значение длины волны Здесь V выражено в В, а — в нм (1нанометр = 10-7 см). При напряжениях V порядка 100В, которые использовались в этих опытах, получаются так называемые «медленные» электроны с порядка 0,1 нм. Эта величина близка к межатомным расстояниям d в кристаллах, которые составляют десятые доли нм и менее. Поэтому получаем ~ d, что дает условие, необходимое для возник-новения дифракции.
Cлайд 10
* Эксперимент Бибермана – Сушкина – Фабриканта по дифракции одиночных электронов {ДАН СССР т.66, №2, с.185 (1949г.)} Вопрос: быть может волновые свойства микрочастиц связаны с тем, что в опытах участ-вуют пучки частиц (e-, p, γ и т.д.), а один e- или γ будут вести себя как “классический шарик”? Ответ: нет, это не так! Скорость e-: Время пролета Интенсивность пучка Время между пролетом двух e- Вероятность, что в приборе одновременно два e- На фотопластинке наблюдалась дифракционная картина от ансамбля одиночных электронов
Cлайд 11
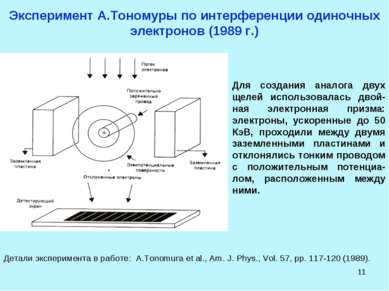
* Эксперимент А.Тономуры по интерференции одиночных электронов (1989 г.) Для создания аналога двух щелей использовалась двой-ная электронная призма: электроны, ускоренные до 50 КэВ, проходили между двумя заземленными пластинами и отклонялись тонким проводом с положительным потенциа-лом, расположенным между ними. Детали эксперимента в работе: A.Tonomura et al., Am. J. Phys., Vol. 57, pp. 117-120 (1989).
Cлайд 12
* Результат эксперимента А. Тономуры Каждая точка обозначает попадание электрона в детектирующий экран. а) 10 электронов; б) 100 электронов; в) 3000 электронов; г) 20 000 электронов; д) 70 000 электронов.
Cлайд 13
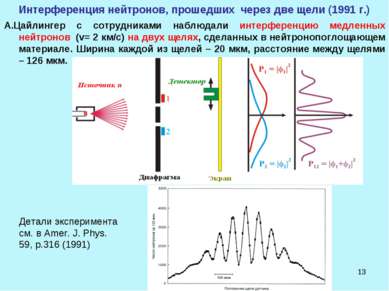
* Интерференция нейтронов, прошедших через две щели (1991 г.) А.Цайлингер с сотрудниками наблюдали интерференцию медленных нейтронов (v= 2 км/с) на двух щелях, сделанных в нейтронопоглощающем материале. Ширина каждой из щелей – 20 мкм, расстояние между щелями – 126 мкм. Детали эксперимента см. в Amer. J. Phys. 59, p.316 (1991)
Cлайд 14
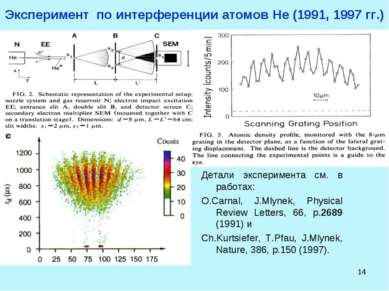
* Эксперимент по интерференции атомов He (1991, 1997 гг.) Детали эксперимента см. в работах: O.Carnal, J.Mlynek, Physical Review Letters, 66, p.2689 (1991) и Ch.Kurtsiefer, T.Pfau, J.Mlynek, Nature, 386, p.150 (1997).
Cлайд 15
Эксперимент по интерференции атомов Na (1991) * Интерферометр состоит из трех дифракционных решеток с периодом 400 нм каждая, расположенных на расстоянии 0.6 м друг от друга. Атомы Na имеют v= 1км/c, что соответствует λ=1,6*10-2 нм. Атомы дифрагируют на 1-ой решетке. Пучки нулевого и первого порядков падают на вторую решетку, на которой они претерпевают дифракцию первого и минус-первого порядков, так, что сходятся на третьей решетке. Первые две решетки образуют интерференционную картину в плоскости третьей решетки, которая используется в качестве экрана. См. детали эксперимента в работе: D.W.Keith et al., Physical Review Letters, 66, p.2693 (1991). Сравните со ссылкой на предыдущем слайде!!!
Cлайд 17
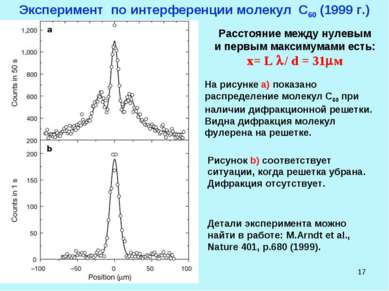
* Эксперимент по интерференции молекул С60 (1999 г.) Расстояние между нулевым и первым максимумами есть: x= L / d = 31 м На рисунке а) показано распределение молекул С60 при наличии дифракционной решетки. Видна дифракция молекул фулерена на решетке. Рисунок b) соответствует ситуации, когда решетка убрана. Дифракция отсутствует. Детали эксперимента можно найти в работе: M.Arndt et al., Nature 401, p.680 (1999).
Дифра
кция части
ц,рассеяние микрочастиц (электронов, нейтронов, атомов и т.п.) кристаллами или молекулами жидкостей и газов, при котором из начального пучка частиц
данного типа
возникают дополнительно отклонённые пучки этих частиц; направление и интенсивность таких отклонённых пучков зависят от строения рассеивающего объекта.
Д. ч. может быть понята лишь на основе квантовой теории. Дифракция — явление волновое, оно наблюдается при распространении волн различной природы: дифракция света, звуковых волн, волн на поверхности жидкости и т.д. Дифракция при рассеянии частиц, с точки зрения классической физики, невозможна.
направлен в сторону распространения волны, или вдоль движения частицы.
Т. о., волновой вектор монохроматической волны, связанной со свободно движущейся микрочастицей, пропорционален её импульсу или обратно пропорционален длине волны.
Поскольку кинетическая энергия сравнительно медленно движущейся частицы
E=
mv 2/2, длину волны можно выразить и через энергию:
При взаимодействии частицы с некоторым объектом — с кристаллом, молекулой и т.п. — её энергия меняется: к ней добавляется потенциальная энергия этого взаимодействия, что приводит к изменению движения частицы. Соответственно меняется характер распространения связанной с частицей волны, причём это происходит согласно принципам, общим для всех волновых явлений. Поэтому основные геометрические закономерности Д. ч. ничем не отличаются от закономерностей дифракции любых волн (см.
Дифракция
волн).
Общим условием
дифракции волн любой природы является соизмеримость длины падающей волны l
с расстоянием
dмежду рассеивающими центрами: l
£
d.
Опыты по дифракции частиц и их квантовомеханическая интерпретация.Первым опытом по Д. ч., блестяще подтвердившим исходную идею квантовой механики — корпускулярно-волновой дуализм, явился опыт американских физиков К.
Дэвиссона
и Л.
Джермера
(1927) по дифракции электронов на монокристаллах никеля (
рис. 2
). Если ускорять электроны электрическим полем с напряжением
V, то они приобретут кинетическую энергию E =
eV, (
е— заряд электрона), что после подстановки в равенство (4) числовых зн
ачений даёт
Здесь
Vвыражено в
в, а l
— в А (1 А = 10 -8
см). При напряжениях
Vпорядка 100
в, которые использовались в этих опытах, получаются так называемые «медленные» электроны с l
порядка 1 А. Эта величина близка к межатомным расстояниям
dв кристаллах, которые составляют несколько А и менее, и соотношение l
£
d, необходимое для возникновения дифракции, выполняется.
Кристаллы обладают
высокой степенью
упорядоченности. Атомы в них располагаются в трёхмерно-периодической кристаллической решётке, т. е. образуют пространственную дифракционную решётку для соответствующих длин волн. Дифракция волн на такой решётке происходит в результате рассеяния на системах пара
ллельных кристаллографических плоскостей, на которых в строгом порядке расположены рассеивающие центры. Условием наблюдения дифракционного максимума при отражении от кристалла является
Брэгга — Вульфа условие
:
2
dsin J
=
nl
, (6)
здесь J
— угол, под которым падает пучок электронов на данную кристаллографическую плоскость (угол скольжения), а
d— расстояние между соответствующими кристаллографическими плоскостями.
В опыте Дэвиссона и Джермера при «отражении» электронов от поверхности кристалла никеля при определённых углах отражения возникали максимумы (
рис. 3
). Эти максимумы отражённых пучков электронов соответствовали формуле (6), и их появление не могло быть объяснено никаким другим путём, кроме как
на основе представлений о волнах и их дифракции; т. о., волновые свойства частиц — электронов — были доказаны экспериментом.
При более высоких ускоряющих электрических напряжениях (десятках
кв) электроны приобретают достаточную кинетическую энергию, чтобы проникать сквозь тонкие плёнки вещества (толщиной порядка 10 -5
см, т. е. тысячи А). Тогда возникает так называемая дифракция быстрых электронов на прохождение, которую на поликристаллических плёнках алюминия и золота впервые исследовали английский учёный Дж. Дж.
Томсон
и советский физик П. С. Тартаковский.
Вскоре после этого удалось наблюдать и явления дифракции атомов и молекул. Атомам с массой
М, находящимся в газообразном состоянии в сосуде при абсолютной температуре
Т, соответствует, по формуле (4), длина волны
Количественно рассеивающую способность атома характеризуют величиной, которая называется атомной амплитудой рассеяния
f(J
), где J
— угол рассеяния, и определяется потенциальной энергией взаимодействия частиц данного сорта с атомами рассеивающего вещества. Интенсивность рассеяния частиц пропорциональна
f 2(J
).
Если атомная амплитуда известна, то, зная взаимное расположение рассеивающих центров — атомов вещества в образце (т. е. зная структуру рассеивающего образца), можно рассчитать общую картину дифракции (которая образуется в результате интерференции вторичных волн, исходящих из рассеивающих центров).
Теоретический расчёт, подтверждённый экспериментальными измерениями, показывает, что атомная амплитуда рассеяния электронов
f эмаксимальна при J
= 0 и спадает с увеличением J
. Величина
f эзависит также от заряда ядра (атомного номера)
Zи от строения электронных оболочек атома, в среднем возрастая с увеличением
Zприблизительно как
Z 1/3для малых J
и как
Z 2/3при больших з
начениях J
, но обнаруживая колебания, связанные с периодическим характером заполнения электронных оболочек.
Атомная амплитуда рассеяния нейтронов
fH для тепловых нейтронов (нейтронов с энергией в сотые доли
эв) не зависит от угла рассеяния, т. е. рассеяние таких нейтронов ядром одинаково во всех направлениях (сферически симметрично). Это объясняется тем, что
атомное ядро
с радиусом порядка 10 -13
смявляется «точкой» для тепловых нейтронов, длина волны которых составляет 10 -8
см. Кроме того, для рассеяния нейтронов нет явной зависимости от заряда ядра
Z. Вследствие наличия у некоторых ядер так называемых резонансных уровней с энергией, близкой к энергии тепловых нейтронов,
fH для таких ядер отрицательны.
Атом рассеивает электроны значительно сильнее, чем рентгеновские лучи и нейтроны: абсолютные значения амплитуды рассеяния электронов
f э
sub>— это величины порядка 10 -8
см, рентгеновских лучей —
f p~
10 -11
см, нейтронов —
fH ~ 10 -12
см. Т. к. интенсивность рассеяния пропорциональна квадрату амплитуды рассеяния, электроны взаимодействуют с веществом (рассеиваются) примерно в миллион раз сильнее, чем рентгеновские лучи (и тем более нейтроны). Поэтому образцами для наблюдения дифракции электронов обычно служат тонкие плёнки толщиной 10 -6 -10 -5
см, тогда как для наблюдения дифракции рентгеновских лучей и нейтронов нужно иметь образцы толщиной в несколько
мм.
Дифракцию на любой системе атомов (молекуле, кристалле и т.п.) можно рассчитать, зная координаты их центров
r iи атомные амплитуды
f iдля данного сорта частиц.
Наиболее ярко эффекты Д. ч. выявляются при дифракции на кристаллах. Однако тепловое движение атомов в кристал
ле несколько изменяет условия дифракции, и интенсивность дифрагированных пучков с увеличением угла J
в формуле (6) уменьшается. При Д. ч. жидкостями, аморфными телами или молекулами газов, упорядоченность которых значительно ниже кристаллической, обычно наблюдается несколько размытых дифракционных максимумов.
Д. ч., сыгравшая в своё время столь
большую роль
в установлении двойственной природы материи — корпускулярно-волнового дуализма (и тем самым послужившая экспериментальным обоснованием квантовой механики), давно уже стала одним из главных рабочих методов для изучения строения вещества. На Д. ч. основаны два важных
современных метода
анализа атомной структуры вещества —
электронография
и
нейтронография
.
Лит.:Блохинцев Д. И., Основы квантовой механики, 4 изд., М., 1963, гл. 1, §
7, 8; Пинскер З. Г., Дифракция электронов, М. — Л., 1949; Вайнштейн Б. К., Структурная электронография, М., 1956; Бэкон Дж., Дифракция нейтронов, пер. с англ., М., 1957; Рамзей Н., Молекулярные пучки, пер. с англ., М., 1960.
Пример 4.1.(С4).Мыльная пленка представляет собой тонкий слой воды, на поверхности которой находится слой молекул мыла, обеспечивающий механическую устойчивость и не влияющий на оптические свойства пленки. Мыльная пленка натянута на квадратную рамку, две стороны которой расположены горизонтально, а две другие — вертикально. Под действием силы тяжести пленка приняла форму клина (см. рисунок), толщина которого внизу оказалась больше, чем вверху. При освещении квадрата параллельным пучком света лазера с длиной волны 666 нм (в воздухе), падающим перпендикулярно пленке, часть света отражается от нее, образуя на ее поверхности интерференционную картину, состоящую из 20 горизонтальных полос. На сколько больше толщина мыльной пленки у основания клина, чем в верхней части, если показатель преломления воды равен ?
Решение.Число полос на пленке определяется разностью хода световой волны в его нижней и верхней частях: Δ = Nλ»/2, где λ»/2 = λ/2n — число полуволн в веществе с показателем преломления n, N — число полос, а Δ — разность толщины пленки в нижней и верхней частях клина.
Отсюда получаем связь между длиной волны лазерного излучения в воздухе λ и параметрами мыльной пленки, из которой следует ответ: Δ = Nλ/2n.
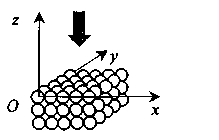
Пример 4.2.(С5).При исследовании структуры кристаллической решетки пучок электронов, имеющих одинаковую скорость, направляется перпендикулярно поверхности кристалла вдоль оси Oz, как показано на рисунке. После взаимодействия с кристаллом отраженные от верхнего слоя электроны распределяются по пространству так, что в некоторых направлениях наблюдаются дифракционные максимумы. В плоскости Ozx имеется такой максимум первого порядка. Какой угол составляет направление на этот максимум с осью Oz, если кинетическая энергия электронов равна 50 эВ, а период кристаллической структуры атомной решетки вдоль оси Ох равен 0,215 нм?
Решение.Импульс р электрона с кинетической энергией Е и массой m равен р =
. Длина волны де-Бройля связана с импульсом λ = =
. Первый дифракционный максимум для решетки с периодом d наблюдается под углом α, удовлетворяющим условию sin α = .
Ответ: sin α =
≈ 0,8, α = 53 o .
Пример 4.3.(С5).При исследовании структуры мономолекулярного слоя вещества пучок электронов, имеющих одинаковую скорость, направляется перпендикулярно исследуемому слою. В результате дифракции на молекулах, образовавших периодическую решетку, часть электронов отклоняется на определенные углы, образуя дифракционные максимумы. С какой скоростью движутся электроны, если первый дифракционный максимум соответствует отклонению электронов на угол α=50° от первоначального направления, а период молекулярной решетки составляет 0,215 нм?
Решение.Импульс р электрона связан с его скоростью р = mv. Длина волны де-Бройля определяется импульсом электрона λ = = . Первый дифракционный максимум для решетки с периодом d наблюдается под углом α, удовлетворяющем условию sin α = = . v =
.
Пример 4.4. (С5).Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает электрон из металлической пластинки (катода) в сосуде, из которого откачан воздух и впущено небольшое количество водорода. Электрон разгоняется постоянным электрическим полем до энергии, равной энергии ионизации атома водорода W= 13,6 эВ, и ионизует атом. Возникший протон ускоряется имеющимся электрическим полем и ударяется о катод. Во сколько раз импульс р m , передаваемый пластинке протоном, больше максимального импульса электрона р е, ионизовавшего атом? Начальную скорость протона считать равной нулю, удар — абсолютно неупругим.
Решение.Энергия Е э, приобретаемая электроном в электрическом поле, равна энергии Е п, приобретаемой протоном, и равна энергии ионизации: Е э = Е п = W. Выражения для импульсов:
протона: р п = m n v n или р п =
;
электрона: р е = m е v е или р е =
; отсюда
.
Пример 4.5. (С6).Для разгона космических аппаратов в открытом космосе и коррекции их орбит предложено использовать солнечный парус — скрепленный с аппаратом легкий экран большой площади из тонкой пленки, которая зеркально отражает солнечный свет. Масса космического аппарата (вместе с парусом) m = 500 кг. На сколько м/с изменится за 24 часа после разворачивания паруса скорость космического аппарата, находящегося на орбите Марса, если парус имеет размеры 100 м х 100 м, а мощность W солнечного излучения, падающего на 1 м 2 поверхности, перпендикулярной солнечным лучам, составляет вблизи Земли 1370 Вт? Считать, что Марс находится в 1,5 раза дальше от Солнца, чем Земля.
Решение.Формула для расчета давления света при его зеркальном отражении: p = . Сила давления: F
=. Зависимость мощности излучения от расстояния до Солнца: (
. Применяя второй закона Ньютона: F = m
а,получаем ответ: Δv =
.
Возможно, будет полезно почитать:
- Что написать в резюме в разделе «обо мне
; - Срок давности по неоплаченным кредитам: какой он
; - Психологическое понимание труда и профессии
; - Как испечь пасхальный кулич – рецепты к пасхе
; - Как испечь пасхальный кулич: мой семейный рецепт с подробными картинками
; - Пустынными тропами Аризоны
; - Пошаговый рецепт морковных оладий: фото и секреты
; - Сколько хранится фаршированный перец в холодильнике
;
Полезные советы
СОВЕТ №1
При чтении статьи об электромагнитном излучении, обратите внимание на то, какие конкретно ученые исследовали эту тему, их квалификацию и опыт в данной области.
СОВЕТ №2
Посмотрите, какие новые технологии или открытия могут быть связаны с этим излучением и как они могут повлиять на нашу повседневную жизнь.

Частые вопросы
Какие свойства имеет «наклонный» пучок электронов?
«Наклонный» пучок электронов обладает особыми свойствами, такими как изменяемый угол наклона, высокая энергия и возможность управления направлением излучения.
Какое значение имеет создание «наклонного» пучка электронов для научных и практических целей?
Создание «наклонного» пучка электронов имеет большое значение для различных областей, включая медицину, физику и технологии, так как он может быть использован для создания рентгеновского излучения, ускорения частиц и других приложений.