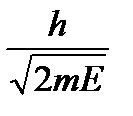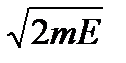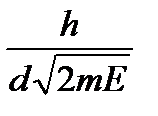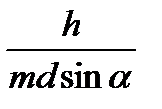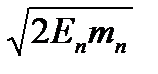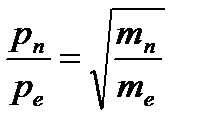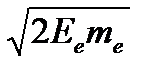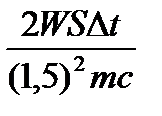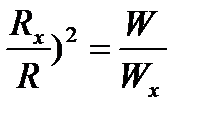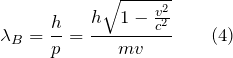Пример 4.1.(С4).Мыльная пленка представляет собой тонкий слой воды, на поверхности которой находится слой молекул мыла, обеспечивающий механическую устойчивость и не влияющий на оптические свойства пленки. Мыльная пленка натянута на квадратную рамку, две стороны которой расположены горизонтально, а две другие — вертикально. Под действием силы тяжести пленка приняла форму клина (см. рисунок), толщина которого внизу оказалась больше, чем вверху. При освещении квадрата параллельным пучком света лазера с длиной волны 666 нм (в воздухе), падающим перпендикулярно пленке, часть света отражается от нее, образуя на ее поверхности интерференционную картину, состоящую из 20 горизонтальных полос. На сколько больше толщина мыльной пленки у основания клина, чем в верхней части, если показатель преломления воды равен ?
Решение.Число полос на пленке определяется разностью хода световой волны в его нижней и верхней частях: Δ = Nλ»/2, где λ»/2 = λ/2n — число полуволн в веществе с показателем преломления n, N — число полос, а Δ — разность толщины пленки в нижней и верхней частях клина.
Отсюда получаем связь между длиной волны лазерного излучения в воздухе λ и параметрами мыльной пленки, из которой следует ответ: Δ = Nλ/2n.
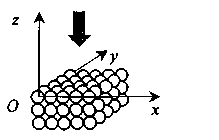
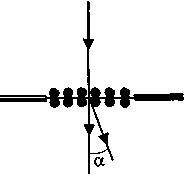
Пример 4.2.(С5).При исследовании структуры кристаллической решетки пучок электронов, имеющих одинаковую скорость, направляется перпендикулярно поверхности кристалла вдоль оси Oz, как показано на рисунке. После взаимодействия с кристаллом отраженные от верхнего слоя электроны распределяются по пространству так, что в некоторых направлениях наблюдаются дифракционные максимумы. В плоскости Ozx имеется такой максимум первого порядка. Какой угол составляет направление на этот максимум с осью Oz, если кинетическая энергия электронов равна 50 эВ, а период кристаллической структуры атомной решетки вдоль оси Ох равен 0,215 нм?
Решение.Импульс р электрона с кинетической энергией Е и массой m равен р =
. Длина волны де-Бройля связана с импульсом λ = =
. Первый дифракционный максимум для решетки с периодом d наблюдается под углом α, удовлетворяющим условию sin α = .
Ответ: sin α =
≈ 0,8, α = 53 o .
Пример 4.3.(С5).При исследовании структуры мономолекулярного слоя вещества пучок электронов, имеющих одинаковую скорость, направляется перпендикулярно исследуемому слою. В результате дифракции на молекулах, образовавших периодическую решетку, часть электронов отклоняется на определенные углы, образуя дифракционные максимумы. С какой скоростью движутся электроны, если первый дифракционный максимум соответствует отклонению электронов на угол α=50° от первоначального направления, а период молекулярной решетки составляет 0,215 нм?
Решение.Импульс р электрона связан с его скоростью р = mv. Длина волны де-Бройля определяется импульсом электрона λ = = . Первый дифракционный максимум для решетки с периодом d наблюдается под углом α, удовлетворяющем условию sin α = = . v =
.
Пример 4.4. (С5).Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает электрон из металлической пластинки (катода) в сосуде, из которого откачан воздух и впущено небольшое количество водорода. Электрон разгоняется постоянным
электрическим полем
до энергии, равной энергии ионизации атома водорода W= 13,6 эВ, и ионизует атом. Возникший протон ускоряется имеющимся электрическим полем и ударяется о катод. Во сколько раз импульс р m , передаваемый пластинке протоном, больше максимального импульса электрона р е, ионизовавшего атом? Начальную скорость протона считать равной нулю, удар — абсолютно неупругим.
Решение.Энергия Е э, приобретаемая электроном в электрическом поле, равна энергии Е п, приобретаемой протоном, и равна энергии ионизации: Е э = Е п = W. Выражения для импульсов:
протона: р п = m n v n или р п =
;
электрона: р е = m е v е или р е =
; отсюда
.
Пример 4.5. (С6).Для разгона космических аппаратов в открытом космосе и коррекции их орбит предложено использовать солнечный парус — скрепленный с аппаратом легкий экран большой площади из тонкой пленки, которая зеркально отражает солнечный свет. Масса космического аппарата (вместе с парусом) m = 500 кг. На сколько м/с изменится за 24 часа после разворачивания паруса скорость космического аппарата, находящегося на орбите Марса, если парус имеет размеры 100 м х 100 м, а мощность W солнечного излучения, падающего на 1 м 2 поверхности, перпендикулярной солнечным лучам, составляет вблизи Земли 1370 Вт? Считать, что Марс находится в 1,5 раза дальше от Солнца, чем Земля.
Решение.Формула для расчета давления света при его зеркальном отражении: p = . Сила давления: F
=. Зависимость мощности излучения от расстояния до Солнца: (
. Применяя второй закона Ньютона: F = m
а,получаем ответ: Δv =
.
D. Ehberger et al. / Phys. Rev. Lett.
Физики из Германии научились получать «наклоненные» фемтосекундные пучки электронов, волновой фронт которых распространяется под углом к направлению движения пучка. Для этого ученые пропускали электроны через тонкое алюминиевое зеркало и светили на них терагерцовым излучением, растягивающим и поворачивающим пучок. Статья опубликована в
Physical Review Letters, кратко о ней сообщает
Physics. Этот результат позволит получить на некоторых типах электронных микроскопов значительно лучшее пространственное и временное разрешение, и даст возможность, например, следить за ходом химических реакций в режиме реального времени.
Исторически ученые используют оптические микроскопы, чтобы изучать небольшие объекты — впервые такие микроскопы были сконструированы еще в начале XVII века, и именно с их помощью биологи открыли одноклеточные организмы и изучили клеточную структуру тканей. К сожалению, возможности таких микроскопов ограничены дифракционным пределом , который не позволяет разрешить объекты с характерным размером много меньше длины волны видимого света (400–750 нанометров). С другой стороны, разрешение микроскопа можно повысить, заменяя фотоны частицами с меньшей длиной волны — например, релятивистскими электронами. Это позволяет увеличить разрешение до десятых долей ангстрема и увидеть отдельные атомы и молекулы.
В
последнее время
физики все больше интересуются не только пространственными, но и временны́ми характеристиками наблюдаемых процессов — например, пытаются увидеть,
какатомы в пространстве или взаимодействуют друг с другом в ходе
химической реакции
. Чтобы ухватить такие особенности, нужно получать «сжатые» пучки электронов, характерное время движения которых (например, время, в течение которого электроны проходят через образец) не превышает характерное время исследуемого процесса. Как правило, это время равно нескольким фемтосекундам (одна фемтосекунда = 10 −15 секунд).
К сожалению, электроны внутри пучка имеют ненулевой
электрический заряд
и отталкиваются друг от друга, в результате чего пучок размывается во времени и пространстве. Из-за этого получить «сжатые» пучки на практике долгое время не удавалось; впервые об успехе сообщили только в 2011 году французские физики-экспериментаторы. Кроме того, такими пучками сложно управлять, и на
данный момент
возможности электронной микроскопии отстают от оптической. Пока что ученые умеют ускорять , сжимать , модулировать и разделять ультракороткие электронные пучки с помощью методов, аналогичных методам оптической микроскопии, однако многие практические приложения требуют более сложной структуры пучков.
Группа исследователей под руководством Питера Баума придумала, как можно «наклонить» волновой фронт фемтосекундного электронного пучка по отношению к направлению его движения. Когда такой «наклоненный» электронный пучок падает перпендикулярно поверхности образца, по ней начинает бежать «волна» энергии с эффективной скоростью
v=
c/tgθ, где
с— скорость пучка, а θ — угол наклона; в обычных пучках (θ = 0°) энергия высвобождается одномоментно. В оптической микроскопии получить «наклоненные» пучки очень просто — достаточно пропустить электромагнитную волну через призму, и из-за дисперсии гармоники с разной частотой будут преломляться на различные углы, формируя наклоненный волновой фронт . Как правило, такие пучки используют для возбуждения образцов. К сожалению, применить этот метод для электронных пучков нельзя.
Схема получения «наклоненного» оптического (сверху) и электронного (снизу) пучка
APS / Alan Stonebraker
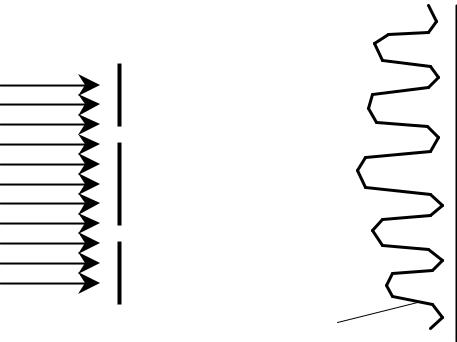
Тем не менее, ученым удалось придумать способ, с помощью которого можно «наклонить» электронный пучок, используя и зеркало из металлической фольги. Суть этого метода заключается в том, что под действием электрического поля электромагнитной волны электроны пучка ускоряются, и его форма изменяется. А поскольку характерное время электромагнитных колебаний (10 −12 секунд) много больше характерного времени прохождения пучка (10 −15 секунд), поле можно считать «застывшим» во времени, а его пространственную часть описывать «мгновенным снимком» электромагнитной волны (на рисунке эта часть представлена синусоидой, которая отражает абсолютную величину вектора напряженности).
Если поле направлено перпендикулярно направлению движения пучка, его передняя и задняя часть также «растаскиваются» в противоположные стороны перпендикулярно движению, и пучок наклоняется. Если же поле направлено вдоль пучка, передняя и задняя части «прижимаются» друг к другу. Чтобы скомбинировать оба эффекта и получить сжатый наклоненный пучок, ученые использовали зеркало из тонкой алюминиевой фольги (толщина около 10 нанометров), которое свободно пропускает электроны и практически полностью отражает терагерцовое излучение. Поворачивая зеркало под нужным углом, исследователи добились того, чтобы продольная и поперечная компоненты электрического поля волны выстроились нужным образом, и повернули волновой фронт электронного пучка по отношению к направлению его движения. Частота электромагнитного излучения при этом составляла 0,3 терагерца, а кинетическая энергия электронов достигала 70 килоэлектронвольт, что отвечает скорости частиц около 0,5 от скорости света.
Искажение формы пучка под действием поперечного (слева) и продольного (справа) электрического поля
APS / Alan Stonebraker
В результате ученым удалось получить пучки с углами наклона вплоть до θ = 10 градусов (при
больших значениях
пучки слишком сильно размывались). Результаты эксперимента при этом хорошо согласовались с теорией. Длина волны таких пучков в сто миллионов раз меньше, чем длина волны оптических «наклоненных» пучков, что позволяет существенно повысить разрешение исследуемых объектов. Кроме того, электроны в пучке ведут себя практически независимо: их пространственная В июле 2016 года физики Андрей Рябов и Питер Баум (два из трех соавторов
новой работы
) новую методику микроскопии, которая основана на фемтосекундных пучках электронов и позволяет увидеть сверхбыстрые колебания электромагнитного поля. В сентябре 2017 года швейцарские исследователи и реализовали на практике метод получения трехмерных изображений нанообъектов с помощью просвечивающей электронной микроскопии; для этого ученые «сжимали» пучки электронов в узкие конусы с помощью системы фокусирующих магнитных линз. А в июле 2018 года американские физики до 0,039 нанометра разрешение изображений, получаемых с помощью просвечивающей электронной микроскопии. Для этого ученые использовали технику птихографии, то есть восстанавливали изображение по
большому числу
дифракционных спектров, полученных при различных параметрах съемки.
Дмитрий Трунин
Дифра
кция части
ц,рассеяние микрочастиц (электронов, нейтронов, атомов и т.п.) кристаллами или молекулами жидкостей и газов, при котором из начального пучка частиц
данного типа
возникают дополнительно отклонённые пучки этих частиц; направление и интенсивность таких отклонённых пучков зависят от строения рассеивающего объекта.
Д. ч. может быть понята лишь на основе квантовой теории. Дифракция — явление волновое, оно наблюдается при распространении волн различной природы: дифракция света, звуковых волн, волн на поверхности жидкости и т.д. Дифракция при рассеянии частиц, с точки зрения классической физики, невозможна.
направлен в сторону распространения волны, или вдоль движения частицы.
Т. о., волновой вектор монохроматической волны, связанной со свободно движущейся микрочастицей, пропорционален её импульсу или обратно пропорционален длине волны.
Поскольку кинетическая энергия сравнительно медленно движущейся частицы
E=
mv 2/2, длину волны можно выразить и через энергию:
При взаимодействии частицы с некоторым объектом — с кристаллом, молекулой и т.п. — её энергия меняется: к ней добавляется потенциальная энергия этого взаимодействия, что приводит к изменению движения частицы. Соответственно меняется характер распространения связанной с частицей волны, причём это происходит согласно принципам, общим для всех волновых явлений. Поэтому основные геометрические закономерности Д. ч. ничем не отличаются от закономерностей дифракции любых волн (см.
Дифракция
волн).
Общим условием
дифракции волн любой природы является соизмеримость длины падающей волны l
с расстоянием
dмежду рассеивающими центрами: l
£
d.
Опыты по дифракции частиц и их квантовомеханическая интерпретация.Первым опытом по Д. ч., блестяще подтвердившим исходную идею квантовой механики — корпускулярно-волновой дуализм, явился опыт американских физиков К.
Дэвиссона
и Л.
Джермера
(1927) по дифракции электронов на монокристаллах никеля (
рис. 2
). Если ускорять электроны электрическим полем с напряжением
V, то они приобретут кинетическую энергию E =
eV, (
е— заряд электрона), что после подстановки в равенство (4) числовых зн
ачений даёт
Здесь
Vвыражено в
в, а l
— в А (1 А = 10 -8
см). При напряжениях
Vпорядка 100
в, которые использовались в этих опытах, получаются так называемые «медленные» электроны с l
порядка 1 А. Эта величина близка к межатомным расстояниям
dв кристаллах, которые составляют несколько А и менее, и соотношение l
£
d, необходимое для возникновения дифракции, выполняется.
Кристаллы обладают
высокой степенью
упорядоченности. Атомы в них располагаются в трёхмерно-периодической кристаллической решётке, т. е. образуют пространственную дифракционную решётку для соответствующих длин волн. Дифракция волн на такой решётке происходит в результате рассеяния на системах пара
ллельных кристаллографических плоскостей, на которых в строгом порядке расположены рассеивающие центры. Условием наблюдения дифракционного максимума при отражении от кристалла является
Брэгга — Вульфа условие
:
2
dsin J
=
nl
, (6)
здесь J
— угол, под которым падает пучок электронов на данную кристаллографическую плоскость (угол скольжения), а
d— расстояние между соответствующими кристаллографическими плоскостями.
В опыте Дэвиссона и Джермера при «отражении» электронов от поверхности кристалла никеля при определённых углах отражения возникали максимумы (
рис. 3
). Эти максимумы отражённых пучков электронов соответствовали формуле (6), и их появление не могло быть объяснено никаким другим путём, кроме как
на основе представлений о волнах и их дифракции; т. о., волновые свойства частиц — электронов — были доказаны экспериментом.
При более высоких ускоряющих электрических напряжениях (десятках
кв) электроны приобретают достаточную кинетическую энергию, чтобы проникать сквозь тонкие плёнки вещества (толщиной порядка 10 -5
см, т. е. тысячи А). Тогда возникает так называемая дифракция быстрых электронов на прохождение, которую на поликристаллических плёнках алюминия и золота впервые исследовали английский учёный Дж. Дж.
Томсон
и советский физик П. С. Тартаковский.
Вскоре после этого удалось наблюдать и явления дифракции атомов и молекул. Атомам с массой
М, находящимся в газообразном состоянии в сосуде при абсолютной температуре
Т, соответствует, по формуле (4), длина волны
Количественно рассеивающую способность атома характеризуют величиной, которая называется атомной амплитудой рассеяния
f(J
), где J
— угол рассеяния, и определяется потенциальной энергией взаимодействия частиц данного сорта с атомами рассеивающего вещества. Интенсивность рассеяния частиц пропорциональна
f 2(J
).
Если атомная амплитуда известна, то, зная взаимное расположение рассеивающих центров — атомов вещества в образце (т. е. зная структуру рассеивающего образца), можно рассчитать общую картину дифракции (которая образуется в результате интерференции вторичных волн, исходящих из рассеивающих центров).
Теоретический расчёт, подтверждённый экспериментальными измерениями, показывает, что атомная амплитуда рассеяния электронов
f эмаксимальна при J
= 0 и спадает с увеличением J
. Величина
f эзависит также от заряда ядра (атомного номера)
Zи от строения электронных оболочек атома, в среднем возрастая с увеличением
Zприблизительно как
Z 1/3для малых J
и как
Z 2/3при больших з
начениях J
, но обнаруживая колебания, связанные с периодическим характером заполнения электронных оболочек.
Атомная амплитуда рассеяния нейтронов
fH для тепловых нейтронов (нейтронов с энергией в сотые доли
эв) не зависит от угла рассеяния, т. е. рассеяние таких нейтронов ядром одинаково во всех направлениях (сферически симметрично). Это объясняется тем, что
атомное ядро
с радиусом порядка 10 -13
смявляется «точкой» для тепловых нейтронов, длина волны которых составляет 10 -8
см. Кроме того, для рассеяния нейтронов нет явной зависимости от заряда ядра
Z. Вследствие наличия у некоторых ядер так называемых резонансных уровней с энергией, близкой к энергии тепловых нейтронов,
fH для таких ядер отрицательны.
Атом рассеивает электроны значительно сильнее, чем рентгеновские лучи и нейтроны: абсолютные значения амплитуды рассеяния электронов
f э
sub>— это величины порядка 10 -8
см, рентгеновских лучей —
f p~
10 -11
см, нейтронов —
fH ~ 10 -12
см. Т. к. интенсивность рассеяния пропорциональна квадрату амплитуды рассеяния, электроны взаимодействуют с веществом (рассеиваются) примерно в миллион раз сильнее, чем рентгеновские лучи (и тем более нейтроны). Поэтому образцами для наблюдения дифракции электронов обычно служат тонкие плёнки толщиной 10 -6 -10 -5
см, тогда как для наблюдения дифракции рентгеновских лучей и нейтронов нужно иметь образцы толщиной в несколько
мм.
Дифракцию на любой системе атомов (молекуле, кристалле и т.п.) можно рассчитать, зная координаты их центров
r iи атомные амплитуды
f iдля данного сорта частиц.
Наиболее ярко эффекты Д. ч. выявляются при дифракции на кристаллах. Однако тепловое движение атомов в кристал
ле несколько изменяет условия дифракции, и интенсивность дифрагированных пучков с увеличением угла J
в формуле (6) уменьшается. При Д. ч. жидкостями, аморфными телами или молекулами газов, упорядоченность которых значительно ниже кристаллической, обычно наблюдается несколько размытых дифракционных максимумов.
Д. ч., сыгравшая в своё время столь
большую роль
в установлении двойственной природы материи — корпускулярно-волнового дуализма (и тем самым послужившая экспериментальным обоснованием квантовой механики), давно уже стала одним из главных рабочих методов для изучения строения вещества. На Д. ч. основаны два важных
современных метода
анализа атомной структуры вещества —
электронография
и
нейтронография
.
Лит.:Блохинцев Д. И., Основы квантовой механики, 4 изд., М., 1963, гл. 1, §
7, 8; Пинскер З. Г., Дифракция электронов, М. — Л., 1949; Вайнштейн Б. К., Структурная электронография, М., 1956; Бэкон Дж., Дифракция нейтронов, пер. с англ., М., 1957; Рамзей Н., Молекулярные пучки, пер. с англ., М., 1960.
ОПРЕДЕЛЕНИЕ
Дифракцией электроновназывают процесс рассеяния данных элементарных частиц на системах частиц вещества. При этом электрон проявляет волновые свойства.
В первой половине XX века Л. де Бройль представил гипотезу о корпускулярно-волновом дуализме различных форма материи. Ученый полагал, электроны наряду с фотонами и другими частицами обладают и корпускулярными и волновыми свойствами. К корпускулярным характеристикам частицы можно отнести: ее энергию (E), импульс (), к волновым параметрам относят: частоту () и длину волны (). При этом волновые и корпускулярные параметры малых частиц связаны формулами:
где h — постоянная Планка.
Каждой частице массы в соответствии с идеей де Бройля, сопоставляется волна, имеющая длину :
Для релятивистского случая:
Дифракция электронов на кристаллах
Первым эмпирическим доказательством, которое подтверждало гипотезу де Бройля был эксперимент американских ученых К Девиссона и Л. Джермера. Они установили, что если пучок электронов рассеивать на кристалле никеля, то получается четкая картина дифракции, которая аналогична картине рассеивания на этом кристалле рентгеновского излучения. Атомные плоскости кристалла играли роль
дифракционной решетки
. Это стало возможным так как при разности потенциалов в 100 В длина волны Де Бройля для электрона равна приблизительно м, это расстояние сравнимо с расстояние между атомными плоскостями используемого кристалла.
Дифракция электронов на кристаллах аналогична дифракции лучей рентгена. Дифракционный максимум отраженной волны появляется при величинах угла Брэгга (), если он удовлетворяет условию:
где d — постоянная решетки кристалла (расстояние между плоскостями отражения); — порядок отражения. Выражение (4) означает то, что максимум дифракции возникает тогда, когда разность хода волн, отражающихся от соседних атомных плоскостей будет равна целому числу длин волн Де Бройля.
Г. Томсон наблюдал картину дифракции электронов на тонкой золотой фольге. На фотографической пластинке, которая находилась за фольгой, были получены концентрические светлые и темные кольца. Радиус колец зависели от скорости движения электронов, которая по Де Бройлю связана с длиной волны. Для установления природы дифрагировавших частиц в данном опыте в пространстве между фольгой и фотографической пластиной создавали магнитное поле. Магнитное поле должно искажать картину дифракции, если картину дифракции создают электроны. Так и случилось.
Дифракцию пучка моноэнергетических электронов на узкой щели, при нормальном падении пучка, можно характеризовать выражением (условие возникновения главных минимумов интенсивности):
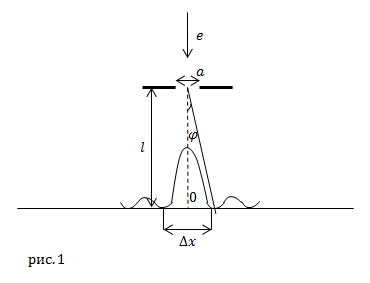
где — угол между нормалью к решетке и направлением распространения дифрагированных лучей; a — ширина щели; k — порядок минимума дифракции; — длина волны де Бройля для электрона.
В середине XX века в СССР был проведен опыт по дифракции на тонкой пленке одиночных электронов, которые летели по очереди.
Так как дифракционные эффекты для электронов наблюдаются только если длина волны, связанная с элементарной частицей имеет такой же порядок как величина расстояния между атомами в веществе, то для изучения структуры вещества применяют метод электонографии, основанный на явлении дифракции электронов. Электронография используется для исследования структур поверхностей тел, так как проникающая способность электронов мала.
При помощи явления дифракции электронов находят расстояния между атомами в молекуле газов, которые адсорбируются на поверхности твердого тела.
Мнение эксперта:
Энциклопедия Примеры решения задач является незаменимым инструментом для обучения и самостоятельной работы. По мнению экспертов, такие энциклопедии предоставляют не только теоретические сведения, но и практические примеры, что делает процесс обучения более наглядным и понятным. Решение задач из энциклопедии позволяет учащимся лучше усвоить материал и применить его на практике. Благодаря разнообразию примеров, представленных в энциклопедии, студенты могут углубить свои знания и научиться применять их в различных ситуациях.

Опыт других людей
Энциклопедия Примеры решения задач — это настоящий помощник для всех, кто сталкивается с математическими задачами. Люди отмечают, что благодаря этой энциклопедии им удалось лучше понять принципы решения задач разной сложности. Они высоко оценивают доступный и понятный язык, в котором изложены материалы, а также обилие примеров, которые помогают усвоить материал на практике. Энциклопедия стала незаменимым инструментом для учеников, студентов и всех, кто хочет улучшить свои знания в математике.
Интересные факты
-
Первая энциклопедия была создана в Китае во II веке до н.э. Она называлась «Эрья» и содержала информацию о различных аспектах китайской культуры, включая историю, географию, науку и литературу.
-
Самая большая энциклопедия в мире — «Википедия». Она содержит более 55 миллионов статей на более чем 300 языках. «Википедия» является свободной энциклопедией, что означает, что любой может редактировать ее статьи.
-
Энциклопедии могут быть использованы для решения задач различного рода. Например, они могут помочь студентам найти информацию для написания рефератов или курсовых работ, а также могут быть использованы для поиска ответов на различные вопросы, возникающие в повседневной жизни.

Примеры решения задач
ПРИМЕР 1
| Задание | Пучок электронов, обладающих одинаковыми энергиями, падает на кристалл, имеющий период нм. Какова скорость электронов (v), если брэгговское отражение первого порядка появляется, если угол скольжения равен ? |
| Решение | За основу решения задачи примем условие возникновения максимума дифракции отраженной волны:
где по условию . Согласно гипотезе де Бройля длина волны электрона равна (для релятивистского случая): Подставим Из (1.3) выразим искомую скорость: где кг — масса электрона; Дж с — постоянная Планка. Проведем вычисления скорости электрона: |
| Ответ |
ПРИМЕР 2
| Задание | Какова скорость электронов в параллельном пучке, если они направлены перпендикулярно на узкую щель, ширина которой равна a? Расстояние от щели до экрана равно l, ширина центрального максимума дифракции . |
| Решение | Сделаем рисунок.
В качестве решения задачи используем условие возникновения главных минимумов интенсивности: |
Схема опыта Дэвиссона–Джермера (1927г.): К – монокристалл никеля; А – источник электронов; В – приёмник электронов; θ – угол отклонения электронных пучков.
Пучок электронов падает перпендикулярно отшлифованной плоскости кристалла S. При поворотах кристалла вокруг оси О гальванометр, присоединённый к приёмнику В, даёт периодически возникающие максимумы
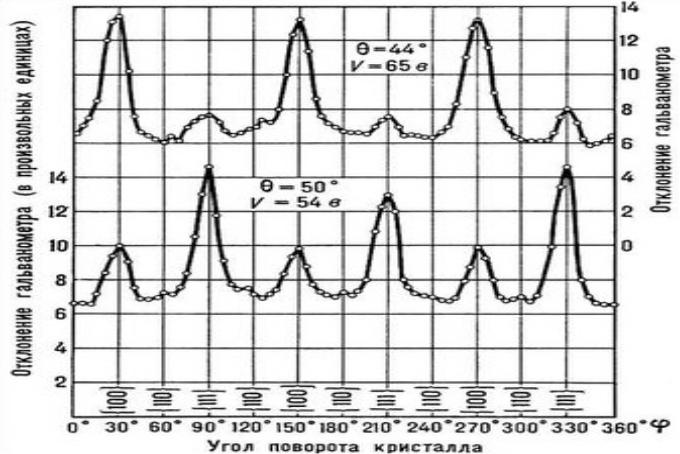
Запись дифракционных максимумов в опыте Дэвиссона–Джермера по дифракции электронов при различных углах поворота кристалла φ для двух значений угла отклонения электронов θ и двух ускоряющих напряжений V
. Максимумы отвечают отражению от различных кристаллографических плоскостей, индексы которых указаны в скобках
Эксперимент с двумя щелями в случае света и электронов
Свет или электроны
Распределение интенсивности на экране
Английский физик
Поль Андриен Морис Дирá к (Paul Adrien Maurice Dirac)
(8.08.1902-1984)
7.2.3. Принцип неопределённостинности
Гейзенберга
Квантовая механика (волновая механика) –
теория, устанавливающая способ описания и законы движения микрочастиц в заданных внешних полях.
Невозможно произвести измерение, не внося в измеряемый объект какое-нибудь возмущение, хотя бы слабое. Сам акт наблюдения вносит существенную неопределённость либо в положение, либо в импульс электрона. В этом и заключается
принцип неопределённости
,
впервые сформулированный Гейзенбергом в
Неравенства Гейзенберга
Dx
Dp
x
³ ,
Dy
Dp
y
³ ,
Dz
Dp
z
³
Dt
× D(E′
— E
)
³
7.2.4.
Волновые функции
ии
В
квантовой механике амплитуду, скажем, электронной волны называют
волновой функцией
и
обозначают греческой буквой «пси»: Ψ.
Таким образом, Ψ задаёт амплитуду нового типа поля, которое можно было бы назвать полем или волной материи, как функцию времени и положения.
Физический смысл функции Ψ заключается в том, что квадрат её модуля даёт плотность вероятности (вероятность, отнесённую к единице объёма) нахождения частицы в соответствующем месте пространства.
|
© А.В. Бармасов, 1998-2013 |
Возможно, будет полезно почитать:
- Заявление о приостановке работы в связи с невыплатой зарплаты
; - Что сказано об увольнении по собственному желанию в п
; - Как восстановить утерянную квитанцию Потерял чек сбербанка можно ли восстановить
; - Где взять номер лицевого счета для заявления на налоговый вычет?
; - Порядок заполнения перечня заявлений о ввозе товаров и уплате косвенных налогов Проверить уплату косвенных налогов в белоруссии
; - Поиск инн организации по названию
; - Дистанционное обучение на бухгалтерских курсах
; - Измерение величин Измеряется s в физике
;
Частые вопросы
Что такое энциклопедия пример?
Энциклопедия представляет систематизированные знания, изложенные в лаконичной форме, по той или иной теме, начиная от научных областей, и заканчивая искусством и популярной культурой. Например, наравне с энциклопедией по физике или истории древнего мира может существовать «Энциклопедия героев Marvel».
Какие бывают энциклопедии для детей?
Какие могут быть энциклопедии?
Энциклопедии делятся на универсальные (например, «Большая советская энциклопедия», «Британника», «Википедия»), отраслевые («Математическая энциклопедия», «Техническая энциклопедия»), региональные, проблемные, персональные.
Что пишут в энциклопедиях?
Энциклопедии содержат структурированные сведения и факты о культуре, истории, науке, искусстве, технологиях и других областях знаний.

Полезные советы
СОВЕТ №1
Перед тем, как начать решать задачи, внимательно изучите теоретический материал по соответствующей теме в энциклопедии. Понимание основных принципов и методов решения задач поможет вам эффективнее применять их на практике.
СОВЕТ №2
Используйте примеры решения задач из энциклопедии как образцы для самостоятельной работы. Попробуйте применить те же методы и подходы к аналогичным задачам, чтобы лучше усвоить материал и развить навыки решения задач.
СОВЕТ №3
Не стесняйтесь обращаться к разделам с подробными пошаговыми решениями задач. Это поможет вам разобраться в сложных моментах и запомнить особенности решения конкретных типов задач.