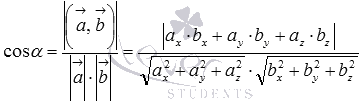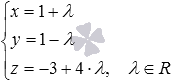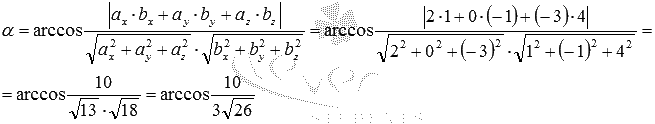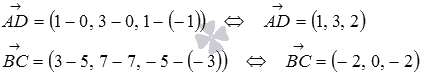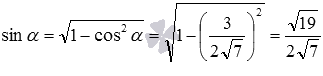В этой статье сначала дадим определение угла между скрещивающимися прямыми и приведем графическую иллюстрацию. Далее ответим на вопрос: «Как найти угол между скрещивающимися прямыми, если известны координаты направляющих векторов этих прямых в прямоугольной системе координат»? В заключении попрактикуемся в нахождении угла между скрещивающимися прямыми при решении примеров и задач.
Навигация по странице.
Угол между скрещивающимися прямыми — определение.
К определению угла между скрещивающимися прямыми будем подходить постепенно.
Сначала напомним определение скрещивающихся прямых: две прямые в трехмерном пространстве называются
скрещивающимися, если они не лежат в одной плоскости. Из этого определения следует, что скрещивающиеся прямые не пересекаются, не параллельны, и, тем более, не совпадают, иначе они обе лежали бы в некоторой плоскости.
Приведем еще вспомогательные рассуждения.
Пусть в трехмерном пространстве заданы две скрещивающиеся прямые a
и b
. Построим прямые a 1
и b 1
так, чтобы они были параллельны скрещивающимся прямым a
и b
соответственно и проходили через некоторую точку пространства M 1
. Таким образом, мы получим две пересекающиеся прямые a 1
и b 1
. Пусть угол между пересекающимися прямыми a 1
и b 1
равен углу . Теперь построим прямые a 2
и b 2
, параллельные скрещивающимся прямым a
и b
соответственно, проходящие через точку М 2
, отличную от точки М 1
. Угол между пересекающимися прямыми a 2
и b 2
также будет равен углу . Это утверждение справедливо, так как прямые a 1
и b 1
совпадут с прямыми a 2
и b 2
соответственно, если выполнить параллельный перенос, при котором точка М 1
перейдет в точку М 2
. Таким образом, мера угла между двумя пересекающимися в точке М
прямыми, соответственно параллельными заданным скрещивающимся прямым, не зависит от выбора точки М
.
Теперь мы готовы к тому, чтобы дать определение угла между скрещивающимися прямыми.
Определение.
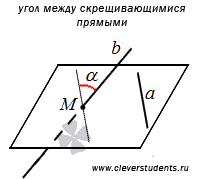
Угол между скрещивающимися прямыми– это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.
Из определения следует, что угол между скрещивающимися прямыми также не будет зависеть от выбора точки M
. Поэтому в качестве точки М
можно взять любую точку, принадлежащую одной из скрещивающихся прямых.
Приведем иллюстрацию определения угла между скрещивающимися прямыми.
Мнение эксперта:
Генетическая символика и оформление задач, связанных с углом между скрещивающимися прямыми, являются важными аспектами математического образования. Эксперты отмечают, что понимание этой темы имеет большое значение для различных областей, включая генетику, инженерию и архитектуру. Определение угла между скрещивающимися прямыми и примеры нахождения этого угла помогают студентам развивать логическое мышление и умение решать задачи. Обозначение скрещивающихся прямых является важным элементом визуализации и анализа геометрических конструкций.

Опыт других людей
Генетическая символика в оформлении задач по математике играет важную роль. Она помогает нам понять, как обозначить скрещивающиеся прямые и решить задачу нахождения угла между ними. Люди отмечают, что понимание генетической символики помогает им лучше освоить этот материал и успешно применять его на практике. Для наглядности приведем примеры нахождения угла между скрещивающимися прямыми, используя генетическую символику.
Интересные факты
-
Генетическая символика— это система обозначений, используемая для представления генетической информации. Она включает в себя символы для генов, аллелей, хромосом и других генетических элементов. Генетическая символика позволяет ученым записывать и обмениваться генетической информацией в краткой и понятной форме.
-
Оформление задач— это процесс преобразования задачи в форму, удобную для решения. Оформление задачи может включать в себя такие шаги, как определение неизвестных, составление уравнений или неравенств, построение графиков или диаграмм. Правильное оформление задачи может значительно упростить ее решение.
-
Угол между скрещивающимися прямыми— это угол, образованный двумя прямыми, которые пересекаются в одной точке. Угол между скрещивающимися прямыми можно найти с помощью формулы:
α = arctan(m2 - m1 / 1 + m1 * m2)
где m1 и m2 — угловые коэффициенты скрещивающихся прямых.

Нахождение угла между скрещивающимися прямыми.
Так как угол между скрещивающимися прямыми определяется через угол между пересекающимися прямым, то нахождение угла между скрещивающимися прямыми сводится к нахождению угла между соответствующими пересекающимися прямыми в трехмерном пространстве.
Несомненно, для нахождения угла между скрещивающимися прямыми подходят методы, изучаемые на уроках геометрии в средней школе. То есть, выполнив необходимые построения, можно связать искомый угол с каким-либо известным из условия углом, основываясь на равенстве или подобии фигур, в некоторых случаях поможет
теорема косинусов
, а иногда к результату приводит
определение синуса, косинуса и тангенса угла
прямоугольного треугольника.
Однако очень удобно решать задачу нахождения угла между скрещивающимися прямыми методом координат. Именно его и рассмотрим.
Пусть в трехмерном пространстве введена Oxyz
(правда, во многих задачах ее приходится вводить самостоятельно).
Поставим перед собой задачу: найти угол между скрещивающимися прямыми a
и b
, которым соответствуют в прямоугольной системе координат Oxyz
некоторые уравнения прямой в пространстве .
Решим ее.
Возьмем произвольную точку трехмерного пространства М
и будем считать, что через нее проходят прямые a 1
и b 1
, параллельные скрещивающимся прямым a
и b
соответственно. Тогда искомый угол между скрещивающимися прямыми a
и b
равен углу между пересекающимися прямыми a 1
и b 1
по определению.
Таким образом, нам осталось найти угол между пересекающимися прямыми a 1
и b 1
. Чтобы применить формулу для нахождения угла между двумя пересекающимися прямыми в пространстве нам нужно знать координаты направляющих векторов прямых a 1
и b 1
.
Как же мы их можем получить? А очень просто. Определение направляющего вектора прямой позволяет утверждать, что множества направляющих векторов параллельных прямых совпадают. Следовательно, в качестве направляющих векторов прямых a 1
и b 1
можно принять направляющие векторы
и
прямых a
и b
соответственно.
Итак,
угол между двумя скрещивающимися прямыми a
и b
вычисляется по формуле
, где
и
— направляющие векторы прямых a
и b
соответственно.
Формула для нахождения косинуса угла между скрещивающимися прямымиa
и b
имеет вид
.
Позволяет найти синус угла между скрещивающимися прямыми, если известен косинус:
.
Осталось разобрать решения примеров.
Пример.
Найдите угол между скрещивающимися прямыми a
и b
, которые определены в прямоугольной системе координат Oxyz
уравнениями
и
.
Решение.
Канонические уравнения прямой в пространстве позволяют сразу определить координаты направляющего вектор этой прямой – их дают числа в знаменателях дробей, то есть,
. Параметрические уравнения прямой в пространстве также дают возможность сразу записать координаты направляющего вектора – они равны коэффициентам перед параметром, то есть,
— направляющий вектор прямой
. Таким образом, мы располагаем всеми необходимыми данными для применения формулы, по которой вычисляется угол между скрещивающимися прямыми:
Ответ:
Угол между заданными скрещивающимися прямыми равен .
Пример.
Найдите синус и косинус угла между скрещивающимися прямыми, на которых лежат ребра AD
и BC
пирамиды АВСD
, если известны координаты ее вершин: .
Решение.
Направляющими векторами скрещивающихся прямых AD
и BC
являются векторы и . Вычислим их координаты как разность соответствующих координат точек конца и начала вектора:
По формуле
мы можем вычислить косинус угла между указанными скрещивающимися прямыми:
Теперь вычислим синус угла между скрещивающимися прямыми:
Генетическая символика
Символика — перечень и объяснение условных названий и терминов, употребляемых в какой-либо отрасли науки.
Основы генетической символики были заложены Грегором Менделем, применившим буквенную символику для обозначения признаков. Доминантные признаки были обозначены заглавными буквами латинского алфавита А, В, С и т.д., рецессивные — малыми буквами — а, в, с и т.д. Буквенная символика, предложенная Менделем, по сути, алгебраическая форма выражения законов наследования признаков.
Для обозначения скрещивания принята следующая символика.
Родители обозначаются латинской буквой Р (Parents — родители), затем рядом записывают их генотипы. Женский пол обозначают сим волом ♂ (зеркало Венеры), мужской — ♀ (щит и копье Марса). Между родителями ставят знак «х», обозначающий скрещивание. Генотип женской особи пишут на первом месте, а мужской — на втором.
Первое по коление обозначается F
1
(Filli — дети), второе поколение — F
2
и т.д. Рядом приводят обозначения генотипов потомков.
Словарь основных терминов и понятий
Аллели (аллельные гены)
— разные формы одного гена, возникшие в результате мутаций и расположенные в одинаковых точках (локусах) парных гомологичных хромосом.
Альтернативные признаки
– взаимоисключающие, контрастные признаки.
Гаметы
(от греч. «
гаметес
» – супруг) – половая клетка растительного или животного организма, несущая один ген из аллельной пары. Гаметы всегда несут гены в «чистом» виде, т.к. образуются путем мейотического деления клеток и содержат одну из пары гомологичных хромосом.
Ген
(от греч. «
генос
» – рождение) – участок молекулы ДНК, несущий информацию о первичной структуре одного конкретного белка.
Гены аллельные
– парные гены, расположенные в идентичных участках гомологичных хромосом.
Генотип
— совокупность наследственных задатков (генов) организма.
Гетерозигота
(от греч. «
гетерос
» – другой и зигота) – зигота, имеющая два разных аллеля по данному гену (
Аа, Вb
).
Гетерозиготными
называют особей, получивших от родительских особей разные гены. Гетерозиготная особь в потомстве дает расщепление по данному признаку.
Гомозигота
(от греч. «
гомос
» – одинаковый и зигота) – зигота, имеющая одинаковые аллели данного гена (оба доминантные или оба рецессивные).
Гомозиготными
называют особей, получивших от родительских особей одинаковые наследственные задатки (гены) по какому-то конкретному признаку. Гомозиготная особь в потомстве не дает расщепления.
Гомологичные хромосомы
(от греч. «
гомос
» – одинаковый) – парные хромосомы, одинаковые по форме, размерам, набору генов. В диплоидной клетке набор хромосом всегда парный: одна хромосома из пары материнского происхождения, вторая – отцовская.
Гетерозиготными
называют особей, получивших от родительских особей разные гены. Таким образом, по генотипу особи могут быть гомозиготными (АА или аа) или гетерозиготными (Аа).
Доминантный признак (ген
) –
преобладающий, проявляющийся – обозначается заглавными буквами латинского алфавита:
А, В,
С и т. д.
Рецессивный признак (ген)
–
подавляемый признак – обозначается соответствующей строчной буквой латинского алфавита:
а, b с
и т. д
Скрещивание анализирующее
– скрещивание испытуемого организма с другим, являющимся по данному признаку рецессивной гомозиготой, что позволяет установить генотип испытуемого.
Скрещивание дигибридное
– скрещивание форм, отличающихся друг от друга по двум парам альтернативных признаков.
Скрещивание моногибридное
– скрещивание форм, отличающихся друг от друга по одной паре альтернативных признаков.
Чистые линии
–
организмы, гомозиготные по одному или нескольким признакам и не дающие в потомстве проявления альтернативного признака.
Фен
– признак.
Фенотип
— совокупность всех внешних признаков и свойств организма, до ступных наблюдению и анализу.
Алгоритм решения генетических задач
- Внимательно прочтите уровень задачи.
- Сделайте краткую запись условия задачи.
- Запишите генотипы и фенотипы скрещиваемых особей.
- Определите и запишите типы гамет, которые образуют скрещиваемые особи.
- Определите и запишите генотипы и фенотипы полученного от скрещивания потомства.
- Проанализируйте результаты скрещивания. Для этого определите количество классов потомства по фенотипу и генотипу и запишите их в виде числового соотношения.
- Запишите ответ на вопрос задачи.
(При решении задач по определённым темам последовательность этапов может изменяться, а их содержание модифицироваться.)
Оформление задач
- Первым принято записывать генотип женской особи, а затем – мужской (
верная запись — ♀ААВВ х ♂аавв; неверная запись
— ♂
аавв х ♀ААВВ). - Гены одной аллельной пары всегда пишутся рядом
(верная запись – ♀ААВВ; неверная запись ♀АВАВ). - При записи генотипа, буквы, обозначающие признаки, всегда пишутся в алфавитном порядке, независимо, от того, какой признак – доминантный или рецессивный – они обозначают (
верная запись — ♀ааВВ;
неверная запись -♀
ВВаа). - Если известен только фенотип особи, то при записи её генотипа пишут лишь те гены, наличие которых бесспорно.
Ген, который невозможно определить по фенотипу, обозначают значком «_»
(например, если жёлтая окраска (А) и гладкая форма (В) семян гороха – доминантные признаки, а зелёная окраска (а) и морщинистая форма (в) – рецессивные, то генотип особи с жёлтыми морщинистыми семенами записывают следующим образом:
А_вв
). - Под генотипом всегда пишут фенотип.
- Гаметы записывают, обводя их кружком
(А). - У особей определяют и записывают типы гамет, а не их количество
Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется
геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).
Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:
группа I — обозначения геометрических фигур и отношений между ними;
группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.
Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.
Группа I
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ
А. Обозначение геометрических фигур
1. Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:
А, В, С, D, … , L, М, N, …
1,2,3,4,…,12,13,14,…
3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
а, b, с, d, … , l, m, n, …
Линии уровня обозначаются: h — горизонталь; f- фронталь.
Для прямых используются также следующие обозначения:
(АВ) — прямая, проходящая через точки А а В;
[АВ) — луч с началом в точке А;
[АВ] — отрезок прямой, ограниченный точками А и В.
4. Поверхности обозначаются строчными буквами греческого алфавита:
α, β, γ, δ,…,ζ,η,ν,…
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α(а || b) — плоскость α определяется параллельными прямыми а и b;
β(d 1 d 2 gα) — поверхность β определяется направляющими d 1 и d 2 , образующей g и плоскостью параллелизма α.
5. Углы обозначаются:
∠ABC — угол с вершиной в точке В, а также ∠α°, ∠β°, … , ∠φ°, …
6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:
Величина угла АВС;
Величина угла φ.
Прямой угол отмечается квадратом с точкой внутри
7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.
Например:
|АВ| — расстояние между точками А и В (длина отрезка АВ);
|Аа| — расстояние от точки А до линии a;
|Аα| — расстояшие от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| расстояние между поверхностями α и β.
8. Для плоскостей проекций приняты обозначения: π 1 и π 2 ,
где π 1 — горизонтальная плоскость проекций;
π 2 -фрюнтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π 3 , π 4 и т. д.
9. Оси проекций обозначаются: х, у, z, где х — ось абсцисс; у — ось ординат; z — ось аппликат.
Постояшную прямую эпюра Монжа обозначают k.
10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:
А», В», С», D», … , L», М», N», горизонтальные проекции точек; А», В», С», D», … , L», М», N», … фронтальные проекции точек; a» , b» , c» , d» , … , l», m» , n» , —
горизонтальные проекции линий; а» ,b» , с» , d» , … , l» , m» , n» , … фронтальные проекции линий; α», β», γ», δ»,…,ζ»,η»,ν»,… горизонтальные проекции поверхностей;
α», β», γ», δ»,…,ζ»,η»,ν»,…
фронтальные проекции поверхностей.
11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса 0α , подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
Так: h 0α — горизонтальный след плоскости (поверхности) α;
f 0α — фронтальный след плоскости (поверхности) α.
12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: H a — горизонтальный след прямой (линии) а;
F a — фронтальный след прямой (линии) a.
13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,2,3,…, n:
А 1 , А 2 , А 3 ,…,А n ;
a 1 , a 2 , a 3 ,…,a n ;
α 1 , α 2 , α 3 ,…,α n ;
Ф 1 , Ф 2 , Ф 3 ,…,Ф n и т. д.
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
A 0 , B 0 , С 0 , D 0 , …
Аксонометрические проекции
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0:
А 0 , В 0 , С 0 , D 0 , …
1 0 , 2 0 , 3 0 , 4 0 , …
a 0 , b 0 , c 0 , d 0 , …
α 0 , β 0 , γ 0 , δ 0 , …
15. Вторичные проекции обозначаются путем добавления верхнего индекса 1:
А 1 0 , В 1 0 , С 1 0 , D 1 0 , …
1 1 0 , 2 1 0 , 3 1 0 , 4 1 0 , …
a 1 0 , b 1 0 , c 1 0 , d 1 0 , …
α 1 0 , β 1 0 , γ 1 0 , δ 1 0 , …
Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.
| № по пор. | Обозначение | Содержание | Пример символической записи |
|---|---|---|---|
| 1 | ≡ | Совпадают | (АВ)≡(CD) — прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки С и D |
| 2 | ≅ | Конгруентны | ∠ABC≅∠MNK — угол АВС конгруентен углу MNK |
| 3 | ∼ | Подобны | ΔАВС∼ΔMNK — треугольники АВС и MNK подобны |
| 4 | || | Параллельны | α||β — плоскость α параллельна плоскости β |
| 5 | ⊥ | Перпендикулярны | а⊥b — прямые а и b перпендикулярны |
| 6 | Скрещиваются | с d — прямые с и d скрещиваются | |
| 7 | Касательные | t l — прямая t является касательной к линии l. βα — плоскость β касательная к поверхности α |
|
| 8 | → | Отображаются | Ф 1 →Ф 2 — фигура Ф 1 отображается на фигуру Ф 2 |
| 9 | S | Центр проецирования. Если центр проецирования несобственная точка, то его положение обозначается стрелкой, указывающей направление проецирования |
— |
| 10 | s | Направление проецирования | — |
| 11 | P | Параллельное проецирование | р s α Параллельное проецирование — параллельное проецирование на плоскость α в направлении s |
| № по пор. | Обозначение | Содержание | Пример символической записи | Пример символической записи в геометрии |
|---|---|---|---|---|
| 1 | M,N | Множества | — | — |
| 2 | A,B,C,… | Элементы множества |
— | — |
| 3 | { … } | Состоит из… | Ф{A, B, C,… } | Ф{A, B, C,… } — фигура Ф состоит из точек А, В,С, … |
| 4 | ∅ | Пустое множество | L — ∅ — множество L пустое (не содержит элементов) | — |
| 5 | ∈ | Принадлежит, является элементом | 2∈N (где N — множество натуральных чисел) — число 2 принадлежит множеству N |
А ∈ а — точка А принадлежит прямой а (точка А лежит на прямой а) |
| 6 | ⊂ | Включает, cодержит | N⊂М — множество N является частью (подмножеством) множества М всех рациональных чисел |
а⊂α — прямая а принадлежит плоскости α (понимается в смысле: множество точек прямой а является подмножеством точек плоскости α) |
| 7 | ∪ | Объединение | С = A U В — множество С есть объединение множеств A и В; {1, 2. 3, 4,5} = {1,2,3}∪{4,5} |
ABCD = ∪ [ВС] ∪ — ломаная линия, ABCD есть объединение отрезков [АВ], [ВС], |
| 8 | ∩ | Пересечение множеств | М=К∩L — множество М есть пересечение множеств К и L (содержит в себе элементы, принадлежащие как множеству К, так и множеству L). М ∩ N = ∅- пересечение множеств М и N есть пустое множество (множества М и N не имеют общих элементов) |
а = α ∩ β — прямая а есть пересечение плоскостей α и β а ∩ b = ∅ — прямые а и b не пересекаются (не имеют общих точек) |
| № по пор. | Обозначение | Содержание | Пример символической записи |
|---|---|---|---|
| 1 | ∧ | Конъюнкция предложений; соответствует союзу «и». Предложение (р∧q) истинно тогда и только тогда,когда р и q оба истинны |
α∩β = { К:K∈α∧K∈β} Пересечение поверхностей α и β есть множество точек (линия), состоящее из всех тех и только тех точек К, которые принадлежат как поверхности α, так и поверхности β |
| 2 | ∨ | Дизъюнкция предложений; соответствует союзу «или». Предложение (p∨q) истинно, когда истинно хотя бы одно из предложений р или q (т. е. или р, или q, или оба). |
— |
| 3 | ⇒ | Импликация — логическое следствие. Предложение р⇒q означает: «если р, то и q» | (а||с∧b||с)⇒a||b. Если две прямые параллельны третьей, то они параллельны между собой |
| 4 | ⇔ | Предложение (р⇔q) понимается в смысле: «если р, то и q; если q, то и р» | А∈α⇔А∈l⊂α. Точка принадлежит плоскости, если она принадлежит некоторой линии, принадлежащей этой плоскости. Справедливо также и обратное утверждение: если точка принадлежит некоторой линии, принадлежащей плоскости, то она принадлежит и самой плоскости |
| 5 | ∀ | Квантор общности, читается: для всякого, для всех, для любого. Выражение ∀(x)P(x) означает: «для всякого x: имеет место свойство Р(х) « |
∀(ΔАВС)( = 180°) Для всякого (для любого) треугольника сумма величин его углов при вершинах равна 180° |
| 6 | ∃ | Квантор существования, читается: существует. Выражение ∃(х)P(х) означает: «существует х, обладающее свойством Р(х)» |
(∀α)(∃a).Для любой плоскости α существует прямая а, не принадлежащая плоскости α и параллельная плоскости α |
| 7 | ∃1 | Квантор единственности существования, читается: существует единственное (-я, -й)… Выражение ∃1(x)(Рх) означает: «существует единственное (только одно) х, обладающее свойством Рх» |
(∀ А, В)(А≠B)(∃1а)(а∋А, В) Для любых двух различных точек А и В существует единственная прямая a, проходящая через эти точки. |
| 8 | (Px) | Отрицание высказывания P(x) | аb(∃α )(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их |
| 9 | \ | Отрицание знака | ≠ -отрезок [АВ] не равен отрезку .а?b — линия а не параллельна линии b |
Возможно, будет полезно почитать:
- Заявление о приостановке работы в связи с невыплатой зарплаты
; - Что сказано об увольнении по собственному желанию в п
; - Как восстановить утерянную квитанцию Потерял чек сбербанка можно ли восстановить
; - Где взять номер лицевого счета для заявления на налоговый вычет?
; - Порядок заполнения перечня заявлений о ввозе товаров и уплате косвенных налогов Проверить уплату косвенных налогов в белоруссии
; - Поиск инн организации по названию
; - Дистанционное обучение на бухгалтерских курсах
; - Измерение величин Измеряется s в физике
;
Частые вопросы
Как найти угол между скрещивающимися прямыми?
Чтобы найти угол между скрещивающимися прямыми, нужно знать, что через каждую из двух скрещивающихся прямых можно провести плоскость, параллельную второй прямой, при том только одну. Чтобы найти угол между скрещивающимися прямыми, нужно найти угол между одной прямой и проекцией другой прямой.
Как найти скрещивающиеся прямые?
Теорема «Признак скрещивающихся прямых» Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Что такое угол между скрещивающимися прямыми?
Можно сказать, что угол между скрещивающимися прямыми — это угол между параллельными им прямыми, лежащими в одной плоскости. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.
Как найти угол между прямыми в параллелепипеде?
Один из интуитивных способов определить угол между диагоналями параллелепипеда — это использовать геометрическую формулу косинуса. Согласно этой формуле, косинус угла между двумя векторами равен скалярному произведению векторов, деленному на произведение их длин.

Полезные советы
СОВЕТ №1
Изучите основные понятия генетической символики, такие как ген, аллель, гомозигота, гетерозигота, доминантный и рецессивный признак. Понимание этих терминов поможет вам лучше освоить материал и правильно оформить задачи.
СОВЕТ №2
Практикуйтесь в определении угла между скрещивающимися прямыми, используя различные методы, например, метод с использованием тригонометрических функций или метод с использованием векторного произведения. Чем больше примеров вы решите, тем лучше вы усвоите этот материал.