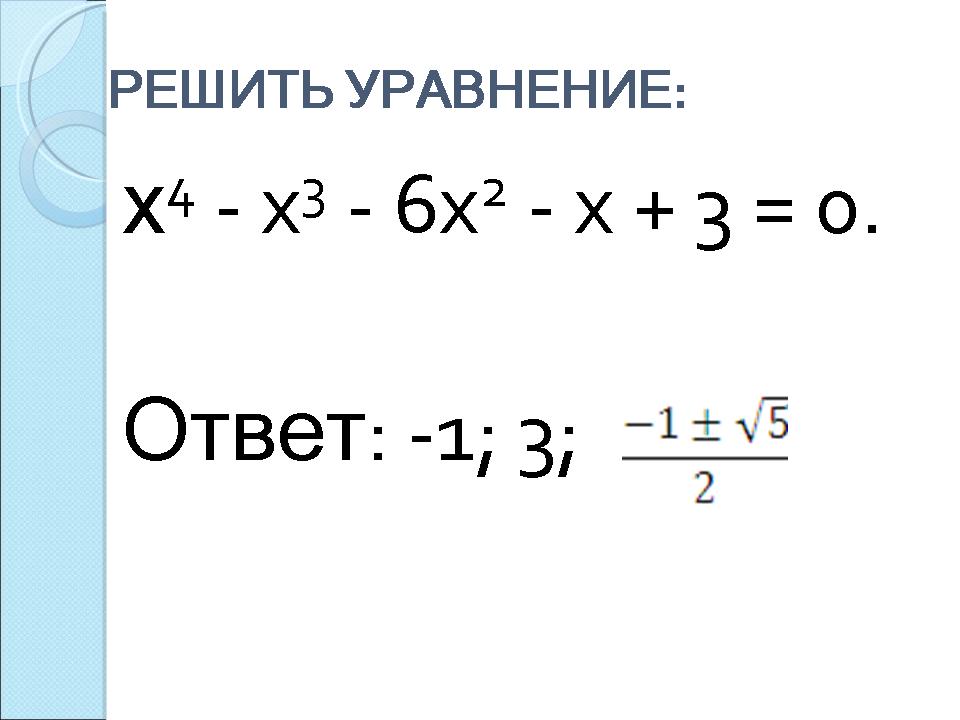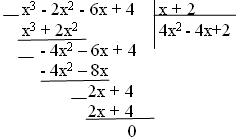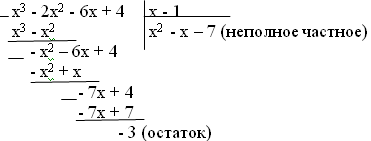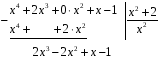III. Примеры задач с решениями

Класс:11

Презентация к уроку

Назад
Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока:

• способствовать развитию навыков деления многочлена на многочлен и использованию схемы Горнера;
• закрепить навыки работы в электронных таблицах OpenOffice.org Calc;
• организовать деятельность учащихся по восприятию, осмысливанию и первичному запоминанию новых знаний;
• разобрать и доказать теорему Безу при решении проблемной ситуации: можно ли разложить многочлен третьей степени на множители;
• рассмотреть использование теорему Безу для решения уравнений высших степеней;
• содействовать развитию
  логического мышления
  , внимания, речи и умения работать самостоятельно.

Тип урока:урок ознакомления с новым материалом.

Оборудование:мультимедиа проектор, презентация к уроку, компьютерный класс.

«Для того, чтобы совершенствовать ум, надо больше рассуждать, чем заучивать».


Декарт (1596 -1650). Французский математик, физик, филолог, философ.

Ход урока

I
. Организационный момент

Наша задача сегодня в
совместной деятельности
подтвердить слова Декарта (слайд 1). Тема нашего урока (слайд 2) «Теорема Безу» настолько значима, что даже используется в
заданиях ЕГЭ
и различных олимпиадах. Теорема Безу облегчает решение многих заданий, содержащих уравнения высших степеней. К сожалению, она изучается только на профильном уровне.

II
. Возникновение проблемной ситуации

На этом уроке мы научимся решать уравнения высших степеней, а алгоритм решения выведем сами.

Решить уравнение:

x 3 – 2x 2 – 6x + 4=0(Слайд 3). Возникает проблема: Мы понимаем, что было бы удобно представить левую часть уравнения в виде произведения, и так как произведение равно нулю, то приравнять к нулю каждый множитель. Для этого надо разложить многочлен 3-ей степени на множители.

Но как?Можно ли сгруппировать или вынести общий множитель за скобку в нашем случае? (Нет).

III
. Актуализация опорных знаний

Вспомним, как разложить на множители многочлен х 2 – 5х – 6? (Слайд 4).

(По формуле разложения на множители квадратного трехчлена:

ах 2 + bх + с = a(x – x 1)(x-x 2), где х 1 и х 2 корни трехчлена).

Найдите корни трехчлена двумя способами. Какими?

(по формуле корней квадратного уравнения и по теореме Виета).

Решают на доске от каждой группы по одному ученику. Остальные учащиеся в тетрадях. Получили: х 2 – 5х – 6 = (х – 6) (х + 1).

Это значит, что трехчлен делится на каждый из двучленов: х – 6 и х + 1.

Обратите внимание на свободный член нашего трехчлена и найдите его делители (±1, ±2, ±3, ±6).

Какие из делителей являются корнями трехчлена? (-1 и 6)

Какой вывод можно сделать?

(Корни трехчлена являются делителями свободного члена).

IV
. Выдвижение гипотезы

Так какой же одночлен поможет подобрать корни многочлена?

Р(х) =
x 3 – 2x 2 – 6x + 4=0?

(Свободный член).

Выпишите его делители: ±1; ±2; ±4.

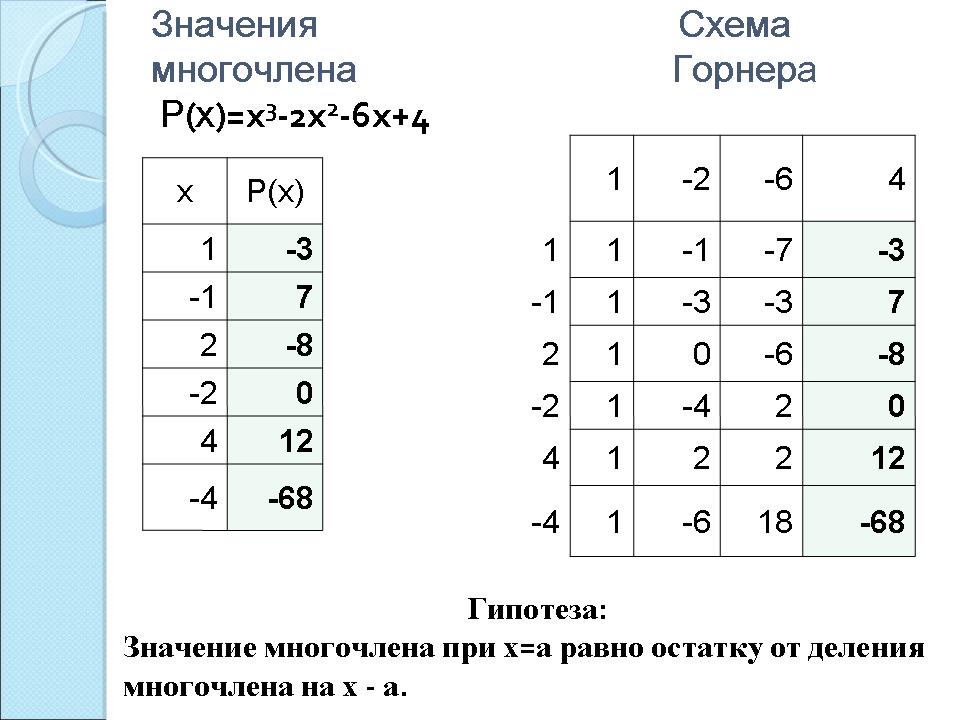
Найдите значения многочлена для каждого делителя. С помощью электронных таблиц и непосредственно:

1 группа вычисляет в тетради, вторая за компьютерами в OpenOffice.org Calc.

Р(1)= -3

Р(-1)=7

Р(2)=-8

Р(-2)=0

Р(4)=12

Р(-4)=-68

(При вычислении в электронных таблицах в ячейку В2 ученики вводят формулу: =А1^3-2*A1^2-6*A1+4. С помощью маркера автозаполнения получают значения многочлена во всем столбце).

Какой из делителей является корнем многочлена? (-2)

Таким образом, один из множителей в разложении будет х-(-2) = x + 2.

Как найти другие множители?

(Разделить «в столбик» на двучлен

х + 2)

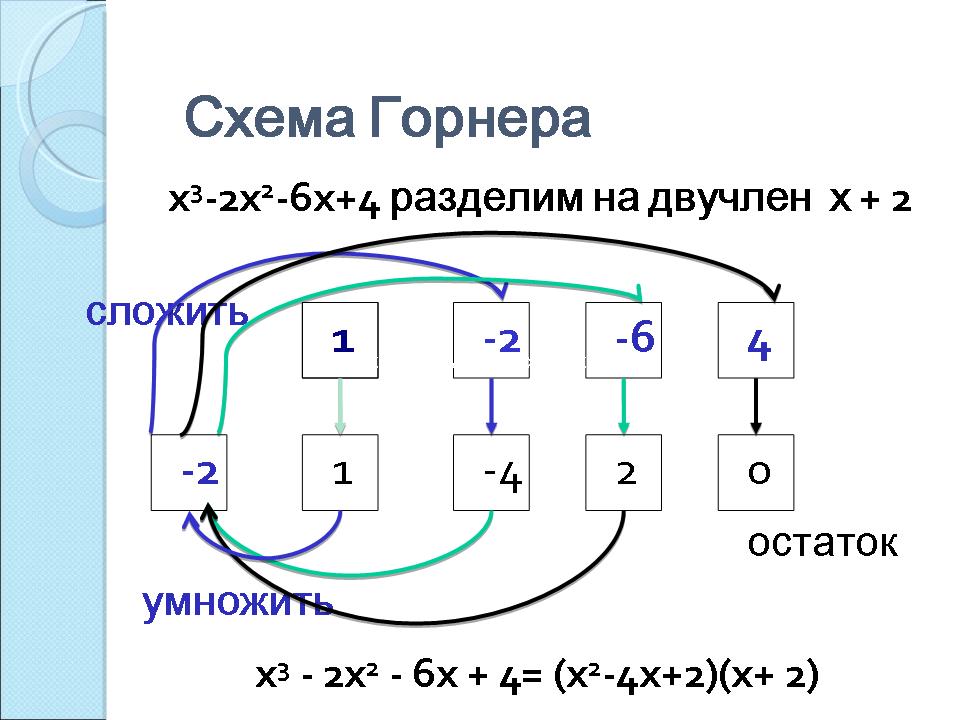
А как еще можно? (по схеме Горнера). (Слайд 5)

Что такое схема Горнера? (

Схема Горнера – это алгоритм деления многочленов, записанный для частного случая, когда делитель равен двучлену

x–a).

Выполняем деление: первая группа «в столбик», вторая – по схеме Горнера.

Разделили без остатка.

Вернемся к уравнению: x 3 – 2x 2 – 6x + 4= (x 2 -4x+2)(x+ 2)=0

x 2 -2x+2=0 – квадратное уравнение. Решите его:

D 1 = 4 – 2 = 2;

Ответ: -2, .

А мог получиться остаток при делении?Ответим на этот вопрос позднее. А сейчас назовите значение многочлена при х = – 2. (Значение равно нулю).

Прошу обратить ваше внимание, что x = – 2 является корнем многочлена и остаток от деления многочлена на х-(-2) равен 0.

Рассмотримх=1 – не является корнем уравнения.

Попробуем разделить многочлен на

х-1. Вторая группа выполняет деление «в столбик». Первая – по схеме Горнера дополняет таблицу ещё одной строкой.

Итак, x 3 – 2x 2 – 6x + 4 = (х – 1)∙(x 2 – х – 7) – 3.

Отметим, что x=1 не является корнем многочлена и остаток от деления многочлена на (х-1) равен значению многочлена при х=1.

Вот и ответ на вопрос об остатке. Да, остаток получился, при таком значении х, которое не является корнем многочлена.

Давайте продолжим схему Горнера для остальных делителей свободного члена. Теперь пусть первая группа вычисляет за компьютером, а вторая в тетрадях.

V
. Доказательство гипотезы

(Слайд 6) Вы заметили закономерность об остатке. Какую? (остаток получился, при таком значении х, которое не является корнем многочлена).

А давайте запишем эту закономерность в
общем виде
.

Пусть Р(х) – многочлен, а – некоторое число.

Докажем утверждение:

Остаток от деления Р(х) на (x – а) равен Р(а).

Доказательство.Разделим Р(х) c остатком на (x – а).

Получим Р(х)= (x – а)Q(х) + R; по определению остатка, многочлен r либо равен 0, либо имеет степень, меньшую степени (x – a), т.е. меньшую 1. Но степень многочлена меньше 1 только в случае, когда она равна 0, и поэтому в обоих случаях R на самом деле является числом – нулем или отличным от нуля.

Подставив теперь в равенство Р(х)= (x – а)Q(х) + R значение x = a, мы получим Р(a)= (a – а)Q(х) + R, P(a) = R, так что действительно R = P(a).

Эту закономерность отметил и математик Безу.

Сообщение ученицы

(Слайд 7) Этьенн Безу – французский математик, член Парижской Академии Наук (с 1758 года), родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года. С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.

Основные работы Этьенна Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений.

В теории решения систем
линейных уравнений
он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках.

Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомный “Курс математики”, написанный им в 1764-69 годах.

Безу развил метод неопределённых множителей. В элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе.

Часть трудов Безу посвящена внешней баллистике.

Именем ученого названа одна из основных теорем алгебры.

Следствие

Какой должен быть остаток, чтобы многочлен Р(х) делился нацело на двучлен (х – а)? (равен 0).

Получаем следствие из теоремы Безу: Для того, чтобы многочлен Р(х) делился нацело на двучлен (х – а), необходимо и достаточно, чтобы выполнялось равенство Р(а) = 0.

VI
.
Усвоение изученного

(Слайд 8) Решить уравнение:

х 4 – x 3 – 6x 2 – x + 3 = 0.

Целые корни многочлена Р(х) = х 4 – x 3 – 6x 2 – x + 3 должны быть делителями свободного члена, так что это могут быть числа -1, 1, 3, -3.

Подберем корень по схеме Горнера:

VII . Итог: Итак, что дает нам Теорема Безу? (Слайд 9) Теорема Безу дает возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого на 1 меньше: если Р(а) = 0, то Р(х)= (x – а)Q(x), и остается решить уравнение Q(x) = 0. Иногда этим приемом – он называется понижением степени – можно найти все корни многочлена.

Ранее
понятие многочлена было определено как
алгебраическая сумма одночленов. Если
все подобные одночлены многочлена
приведены и расположены в порядке
убывания степени переменной, то полученная
запись называется

канонической
формой записимногочлена.

Определение.Выражение вида

где

x– некоторая переменная,
действительные
числа, причем
,
называется

многочленом
степени
n
от переменной
x
.
Степеньюмногочлена является наибольшая степень
переменной в его канонической записи.
Если переменная не встречается в записи
многочлена, т.е. многочлен равен константе,
его степень считается равной 0. Случай,
когда многочлен
необходимо рассматривать отдельно. В
этом случае принято считать, что его
степень не определена.

Примеры.многочлен
второй степени,

многочлен
пятой степени.

Определение.Два многочлена

равнытогда и только тогда, когда у них в
канонических формах при одинаковых
степенях стоят одинаковые коэффициенты.

Определение.
Число
называется

корнем
многочлена,
если при постановке этого числа вместо

xмногочлен принимает значение 0, т.е.
Другими
словами,
будет являться корнем уравнения

Таким
образом, задача отыскания всех корней
многочлена и корней рационального
уравнения – одна и та же задача.

Рациональные
уравнения первой и второй степени
решаются по известным алгоритмам.
Существуют также формулы отыскания
корней многочленов третьей и четвертой
степени (формулы Кардано и Феррари),
однако в силу их громоздкости они не
входят в курс элементарной математики.

Общей
идеей отыскания корней многочленов
высших степеней является разложение
многочлена на множители и замена
уравнения равносильной ему совокупностью
уравнений более низкой степени.

В
предыдущих темах отмечались основные
способы разложения многочленов на
множители: вынесение общего множителя;
группировка; формулы сокращенного
умножения.

Однако
способ группировки не носит алгоритмического
характера, поэтому его трудно применять
для многочленов больших степеней.
Рассмотрим некоторые дополнительные
теоремы и методы, позволяющие раскладывать
на множители многочлены высших степеней.

Теорема
о делении с остатком.Пусть даны многочлены
,
причем степень
отлична от 0, и степень
больше степени
.
Тогда существуют многочлены
,
такие, что выполняется равенство

Причем,
степень
меньше степени
Многочлен
называется

делимым,
многочлен

делителем,многочлен

неполным
частным,
а многочлен

остатком.

Если
остаток от деления равен 0, то говорят,
что

делитсяна

нацело,
при этом равенство принимает вид:

Алгоритм
деления многочлена на многочлен
аналогичен алгоритму деления числа на
число столбиком или уголком. Опишем
шаги алгоритма.

Записать
делимое в строчку, включая все степени
переменной (те, которые отсутствуют,
записать с коэффициентом 0).

Записать
в «уголке» делимое, включая все степени
переменной.

Чтобы
найти первое слагаемое (одночлен) в
неполном частном, нужно старший одночлен
делимого разделить на старший одночлен
делителя.

Полученное
первое слагаемое частного умножить на
весь делитель и результат записать под
делимым, причем одинаковые степени
переменной записать друг под другом.

Из
делимого вычесть полученное произведение.

К
полученному остатку применить алгоритм,
начиная с пункта 1).

Алгоритм
завершен, когда полученная разность
будет иметь степень меньше степени
делителя. Это – остаток.

Пример.
Разделить многочлен
на
.

Записываем
делимое и делитель

Повторяем
процедуру

Степень
меньше степени делителя. Значит, это –
остаток. Результат деления запишется
так:

Схема
Горнера.Если делителем является многочлен
первой степени, то процедуру деления
можно упростить. Рассмотрим алгоритм
деления многочлена
на двучлен
.

Пример.
Разделить по схеме Горнера многочлен
на
.
В этом случае

а=2.
Выпишем по шагам результаты выполнения
алгоритма.

Шаг
первый.

Шаг
второй

Шаг
третий

Шаг
четвертый

Таким
образом, результат деления запишем так

Замечание.Если необходимо выполнить деление на
двучлен

То
его преобразовывают к виду
тогда
.
Отсюда видно, что, разделив по схеме
Горнера
на
мы найдем
Тогда искомое частное
получится делением найденного на

а.
Остаток остается таким же.

Теорема
Безу.
Остаток от деления многочлена
на
равен значению многочлена в точке

x=

а,
т.е.
.
Многочлен
делится
на
без остатка тогда и только тогда, когда

x=

аявляется корнем многочлена
.

Таким
образом, найдя один корень многочлена


а
,
можно его разложить на множители
,
выделив множитель
,
имеющий степень на единицу меньше
степени
.
Найти этот множитель можно либо по схеме
Горнера, либо делением «уголком».

Вопрос
о нахождении корня решается либо
подбором, либо с использованием теоремы
о рациональных корнях многочлена.

Теорема.Пусть многочлен
имеет целые коэффициенты. Если несократимая
дробь
является корнем многочлена, то ее
числитель

pявляется делителем свободного члена
,
а знаменатель

qявляется делителем старшего коэффициента
.

Эта
теорема лежит в основании

алгоритма
поиска рациональных корнеймногочлена (если они есть).

Разложение
алгебраической дроби в сумму простейших
дробей

ОпределениеДробь, в числителе и в знаменателе
которой стоят многочлены, называется

алгебраической
дробью.

Рассмотрим
алгебраические дроби от одной переменной.
Их в общем виде можно записать так:
,
где в числителе стоит многочлен степени

n,
в знаменателе – многочлен степени

k.
Если
,
то дробь называется

правильной.

К

простейшим
алгебраическим дробямотносятся правильные дроби двух видов:

Теорема.Любую алгебраическую дробь можно
представить в виде суммы простейших
алгебраических дробей.

Алгоритм
разложения алгебраической дроби в сумму
простейших дробей.

Разложить
знаменатель на множители.

Определить
количество правильных дробей и вид их
знаменателей.

Записать
равенство, в левой части которого –
исходная дробь, в правой – сумма
простейших дробей с неопределенными
коэффициентами.

Привести
дроби в правой части к общему знаменателю.

Приравнять
многочлены, стоящие в числителях дробей.
Пользуясь определением равенства
многочленов, составить систему линейных
уравнений и решить ее, найдя неопределенные
коэффициенты.

Теорема Безу, невзирая на кажущуюся простоту и очевидность, является одной из базовых теорем теории многочленов . В данной теореме алгебраические характеристики многочленов (они позволяют работать с многочленами как с целыми числами) связываются с их
функциональными характеристиками
(которые позволяют рассматривать многочлены как функции).

Теорема Безуутверждает, что остаток от деления многочлена на многочлен – это .

Коэффициенты многочлена лежат в неком коммутативном кольце с единицей (к примеру, в поле вещественных либо комплексных чисел).

Мнение эксперта:

Эксперты отмечают, что примеры задач с решениями играют важную роль в процессе обучения. Они помогают студентам лучше понять материал и применить его на практике. Правильно подобранные примеры могут стимулировать мышление, развивать аналитические навыки и способствовать углубленному усвоению информации. Кроме того, решение задач позволяет проверить свои знания и навыки, что способствует повышению уверенности в своих силах. Важно, чтобы примеры были разнообразными и интересными, чтобы стимулировать учеников к активному участию в учебном процессе.

https://www.youtube.com/embed/JjuCCqgzuK4

Теорема Безу – доказательство.

Делим с остатком многочлен

P(x)на многочлен

(x-a):

Исходя из того, что

deg R(x) – многочлен степени не выше нуля. Подставляем , так как , получаем
.

Но наиболее важна не именно теорема, а следствие теоремы Безу:

1. Число – корень многочлена

P(x)тогда и только тогда, когда

P(x)делится без остатка на двучлен

x-a.

Исходя из этого – множество корней многочлена

P(x)тождественно множеству корней соответствующего уравнения

x-a.

2. Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (когда старший коэффициент равен единице – все рациональные корни целые).

3. Предположим, что – целый корень приведенного многочлена

P(x)с целыми коэффициентами. Значит, для любого целого число делится на .

Теорема Безу дает возможность, найдя один корень многочлена, искать дальше корни многочлена, степень которого уже на 1 меньше: если , то данный многочлен

P(x)будет выглядеть так:

Теорема Безу примеры:

Найти остаток от деления многочлена на двучлен .

Теорема Безу примеры решения:

Исходя из теоремы Безу, искомый остаток соответствует значению многочлена в точке . Тогда найдем , для этого значение подставляем в выражение для многочлена вместо . Получаем:

Ответ: Остаток = 5.

Интересные факты

1. Задача о трех домах и трех колодцах.

В некотором городе есть три дома и три колодца. Каждый дом находится на одинаковом расстоянии от каждого колодца. Требуется провести от каждого дома к каждому колодцу по одной трубе так, чтобы трубы не пересекались.

Решение:

Для решения этой задачи можно использовать метод графов. Построим граф, в котором вершинами будут дома и колодцы, а ребрами – возможные пути между ними. Затем найдем в этом графе минимальное остовное дерево, которое соединит все вершины графа с минимальной общей длиной ребер. Это и будет решением задачи.

2. Задача о рюкзаке.

У вас есть рюкзак, в который можно положить определенное количество предметов. Каждый предмет имеет свой вес и свою ценность. Требуется выбрать такие предметы, чтобы их общий вес не превышал вместимости рюкзака, а их общая ценность была максимальной.

Решение:

Для решения этой задачи можно использовать динамическое программирование. Сначала построим таблицу, в которой для каждого предмета и каждого возможного веса рюкзака будет храниться максимальная ценность предметов, которые можно положить в рюкзак с данным весом. Затем, начиная с последнего предмета, будем заполнять таблицу, используя значения из предыдущих строк. В конце в таблице будет храниться максимальная ценность предметов, которые можно положить в рюкзак с данным весом.

3. Задача о коммивояжере.

У вас есть список городов и расстояния между ними. Требуется найти кратчайший маршрут, который посетит каждый город ровно один раз и вернется в исходный город.

Решение:

Для решения этой задачи можно использовать алгоритм ближайшего соседа. Начинаем с произвольного города и на каждом шаге переходим в ближайший город, который еще не был посещен. Когда все города будут посещены, возвращаемся в исходный город. Этот алгоритм не всегда находит оптимальное решение, но он обычно дает достаточно хорошее приближение к нему.

https://www.youtube.com/embed/eiwZY1oXGvo

Опыт других людей

“III. Примеры задач с решениями” – это уникальный и полезный ресурс, который помогает людям разобраться с сложными задачами и найти правильные решения. Многие пользователи отмечают, что благодаря этому ресурсу им удалось значительно улучшить свои навыки в решении задач и углубить понимание математики, физики и других предметов. Они высоко ценят доступность материала, понятные объяснения и разнообразие примеров, которые помогают им успешно справляться с учебными заданиями. III. Примеры задач с решениями – это надежный помощник для всех, кто стремится к академическому успеху и развитию своих интеллектуальных способностей.

Схема Горнера.

Схема Горнера– это алгоритм деления (деление схемой Горнера) многочленов, записываемый для частного случая, если частное равно двучлену .

Построим этот алгоритм:

Предположим, что – делимое

Частное (его степень, вероятно, будет на удиницу меньше),

r– остаток (т.к. деление осуществляется на многочлен

1-ойстепени, то степень остатка будет на единицу меньше, т.е. нулевая, таким образом, остаток это константа).

По определению деления с остатком

P(x) = Q(x) (x-a) + r. После подстановки выражений многочленов получаем:

Раскрываем скобки и приравниваем коэффициенты при одинаковых степенях, после чего выражаем коэффициенты частного через коэффициенты делимого и делителя:

Удобно вычисления сводить в такую таблицу:

В ней выделены те клетки, содержимое которых участвует в вычислениях на очередном шаге.

Схема Горнера примеры:

Пусть надо поделить многочлен на двучлен

x-2.

Составляем таблицу с двумя строками. В 1 строку выписываем коэффициенты нашего многочлена. Во второй строке будем получать коэффициенты неполного частного по следующей схеме: в первую очередь переписываем старший коэффициент данного многочлена, далее, дабы получить очередной коэффициент, умножаем последний найденный на

а=2и складываем с соответствующим коэффициентом многочлена

F(x). Самый последний коэффициент будет остатком, а все предыдущие – коэффициентами неполного частного.

Число является корнем многочлена тогда и только тогда, когда делится на

Пусть _ корень многочлена, т.е. Разделим на, где степень меньше степени, которая равна Значит, степень равна, т.е. . Значит, . Так как, то из последнего равенства следует, что т.е. .

Обратно, пусть делит, т.е. . Тогда.

Следствие.Остаток от деления многочлена на равен.

Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена равносильно разысканию его линейных делителей со старшим коэффициентом 1.

Многочлен можно разделить на линейный многочлен с помощью алгоритма деления с остатком, но существует более
удобный способ
деления, известный под названием схемы Горнера.

Пусть и пусть, где. Сравнивая коэффициенты при одинаковых степенях неизвестной с левой и
правой частях
последнего равенства, имеем:

Число называется корнем кратности многочлена, если делит, но уже не делит.

Чтобы поверить, будет ли число корнем многочлена и какой кратности, можно воспользоваться схемой Горнера. Сначала делится на затем, если остаток равен нулю, полученное частное делится на и т.д. до получения не нулевого остатка.

Число различных корней многочлена не превосходит его степени.

Большое значение имеет следующая основная теорема.

Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).

Следствие. Всякий многочлен степени имеет в C (множестве комплексный чисел) столько корней, какова его степень, считая каждый корень столько раз, какова его кратность.

где _ корни, т.е. во множестве C всякий многочлен разлагается в произведение линейных множителей. Если одинаковые множители собрать вместе, то:

где уже различные корни, _ кратность корня.

Если многочлен, с действительными коэффициентами имеет корень, то число также корень

Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.

Следствие.Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.

Пусть и корни Тогда делится на и но так как у и нет
общих делителей
, то делится на прозведение.

Утверждение 2.Многочлен с действительными коэффициентами степени всегда разлагается на множестве действительных чисел в произведение линейных многочленов, отвечающих его вещественным корням, и многочленов 2-ой степени, отвечающих паре сопряженных комплексных корней.

При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.

Рациональной дробью называется дробь где и _ многочлены с действительными коэффициентами, причем многочлен. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя. Если рациональная дробь не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде, где и – некоторые многочлены, а – правильная рациональная дробь.

Лемма 1.Если – правильная рациональная дробь, а число является вещественным корнем кратности многочлена, т.е. и, то существует вещественное число и многочлен с вещественными коэффициентами, такие, что где дробь также является правильной.

При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.

Лемма 2.Если – правильная рациональная дробь, а число (и – вещественные,) является корнем кратности многочлена, т.е. и, и если, то существуют вещественные числа и и многочлен с вещественными коэффициентами, такие, что где дробь также является правильной.

Рациональные дроби вида, _ трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.

Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.

При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов. Он состоит в следующем:

• · Для данной дроби пишется разложение, в котором коэффициенты считаются неизвестными;
• · После этого обе части равенства приводятся к общему знаменателю и у получившихся в числителе многочленов приравниваются коэффициенты.

При этом если степень многочлена равна, то в числителе после приведения к общему знаменателю получается многочлен степени, т.е. многочлен с коэффициентами.

Число неизвестных также равняется: .

Таким образом, получается система уравнений с неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.

Возможно, будет полезно почитать:

• Тюменское высшее военно-инженерное командное училище имени маршала инженерных войск А
  ;
• Почему ссср ввязался в гражданскую войну в испании Испанская гражданская война 1936 1939 кратко
  ;
• Савинов, Пётр Иванович: биография Капитан вов савинов п и танкист ас
  ;
• Методы решения неопределенных интегралов
  ;
• Основные проблемы, изучаемые на макроэкономическом уровне
  ;
• Свинья скорпион карьера и финансы
  ;
• Как производится расчет пени по налогам: начисление пени, порядок расчета, пример вычислений
  ;
• Дарение полностью самортизированного объекта ОС
  ;

Задача на нахождение части от числа. Как решать задачи с дробями?

Полезные советы

СОВЕТ №1

Изучите примеры задач с решениями внимательно и не спешите сразу смотреть ответы. Попробуйте решить задачу самостоятельно, а затем сравните свое решение с предложенным.

СОВЕТ №2

После изучения примеров задач с решениями, попробуйте решить похожие задачи самостоятельно. Это поможет вам закрепить материал и лучше понять принципы решения подобных задач.

СОВЕТ №3

Не бойтесь задавать вопросы, если что-то непонятно. Обсуждение задач с решениями с другими людьми или преподавателем может помочь вам лучше усвоить материал и найти новые подходы к решению задач.

Частые вопросы

Какие примеры задач могут быть рассмотрены в статье “III. Примеры задач с решениями”?

В статье “III. Примеры задач с решениями” могут быть рассмотрены различные математические, физические, экономические или другие задачи, для которых предлагаются подробные решения.

Какие методы и подходы к решению задач могут быть представлены в статье “III. Примеры задач с решениями”?

В статье “III. Примеры задач с решениями” могут быть представлены различные методы и подходы к решению задач, такие как математические модели, численные методы, аналитические решения, оптимизационные подходы и другие.