В задачах по геометрии часто требуется вычислить площадь многоугольника. Причем он может иметь довольно разнообразную форму — от всем знакомого треугольника до некоторого n-угольника с каким-то невообразимым числом вершин. К тому же эти многоугольники бывают выпуклыми или вогнутыми. В каждой конкретной ситуации полагается отталкиваться от
внешнего вида
фигуры. Так получится выбрать оптимальный путь решения задачи. Фигура может оказаться правильной, что существенно упростит решение задачи.
А также из многих других примеров мы видим, как эта геометрическая поверхность поверхности рисует свое интуитивное происхождение из множества
практических опытов
и потребностей. Более того, весь этот комплекс теорий, которые сегодня идут под названием «геометрия», первоначально был рожден из необходимости того, чтобы фермеры могли оценить расширение, величину поля.
В общей концепции подразумевается, что если рассматривать две или более поверхности поверхности, общая площадь равна сумме частичных областей отдельных частей, что выражается в том, что область обладает аддитивным свойством. Так что, если фигура содержит целую секунду, говорят, что у нее есть «небольшая область первой».
Немного теории о многоугольниках
Если провести три или более пересекающихся прямых, то они образуют некоторую фигуру. Именно она является многоугольником. По количеству точек пересечения становится ясно, сколько вершин у него будет. Они дают название получившейся фигуре. Это может быть:
Такая фигура непременно будет характеризоваться двумя положениями:
Учитывая эти фундаментальные свойства, площадь поверхности поверхности, таким образом, имеет большую величину. Чтобы оценить это, нам придется сравнить его с определенной областью, фиксированной раз и навсегда, которая будет приниматься за единицу измерения, с. например, площадь квадрата с одним метром, отношение между площадью, подлежащей оценке, и этим устройством будет числом, которое, как говорят, является мерой самой площади.
Прямые плоские плоскости. — Задаваемая по размеру проблема легко решается для всех плоских областей, ограниченных прямыми сегментами или полигонами, как это обычно называют. Достаточно разбить многоугольник, рассматриваемый во многих треугольниках, с помощью диагональной системы, отдельно оценить площадь каждого из этих треугольников, а затем сделать сумму всех этих частичных областей, чтобы иметь общую площадь многоугольника.
- Смежные стороны не принадлежат одной прямой.
- У несмежных отсутствуют общие точки, то есть они не пересекаются.
Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.
Таким образом, мы пытаемся разрезать треугольник, рассматриваемый на столько частичных многоугольников, а затем переконфигурировать с ними другую фигуру, которая, очевидно, будет иметь ту же площадь треугольника треугольник, но который легче измерим; р. эс. прямоугольник высоты, равный квадрату единицы измерения, и удобное основание.
Это всегда можно выполнить с помощью конечного числа геометрических конструкций, исполняемых с линией и компасом, а также с проблемой измерения области многоугольника, которая разрешима с этими элементарными операциями. Как мы видим, эта проблема подняла эту теорию, столь важную в элементарной геометрии, что изучала преобразования в двух других эквивалентных многоугольниках, т.е. суммы равных многоугольников и, следовательно, одной и той же области.
Мнение эксперта:
Площадь многоугольника можно найти с помощью формулы, которая зависит от его формы. Для прямоугольника площадь вычисляется как произведение длины на ширину: S = a * b, где a и b — длины сторон. Это основная теорема, которая позволяет быстро и точно определить площадь прямоугольника. Для других многоугольников существуют более сложные формулы, но основной принцип остается тем же – разбить фигуру на более простые части и вычислить их площади, а затем сложить результаты. Это важное математическое умение, которое находит применение не только в учебе, но и в повседневной жизни.

Какие их виды существуют?
Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по
разные стороны
от прямой, проведенной через произвольную сторону многоугольника. В выпуклом всегда все вершины лежат с одной стороны от такой прямой.
Пей-регулярные многоугольники, площадь А получается из формулы А =. Или по формуле. Другие плоские фигуры. — Если вы хотите измерить площадь плоских плоскостей не только от прямых сегментов, но и от кривых, полностью или частично, проблема становится намного сложнее. Как и в предыдущей задаче измерения многоугольника, ее можно считать Происхождение хорошей части элементарной геометрии, и особенно теории эквивалентности, от проблемы меры изогнутых плоских фигур, имело первое происхождение этой обширной ветви высшей математики, а точнее от вычисления бесконечно малых, которое идет под названием интегрального расчета.
В школьном курсе геометрии
большая часть
времени уделяется именно выпуклым фигурам. Поэтому в задачах требуется узнать площадь выпуклого многоугольника. Тогда существует формула через радиус описанной окружности, которая позволяет найти искомую величину для любой фигуры. В других случаях однозначного решения не существует. Для треугольника формула одна, а для квадрата или трапеции совершенно другие. В ситуациях, когда фигура неправильная или вершин очень много, принято разделять их на простые и знакомые.
Существенное различие заключается в том, что, хотя в случае полигонов оценка области всегда может быть выполнена, как мы уже говорили, с конечным числом операций, в случае, если теперь считать это невозможным, более неспособным сократить цифры ограниченные кривыми в конечном числе элементарных многоугольников, поэтому необходимо определить целый ряд значений, более или менее приближенных, искомой области и только предельное число, к которому мы все чаще приближаемся к неопределенному появлению этих определений, может представлять
точное значение
искомой области.
Интересные факты
- Площадь прямоугольника можно найти, умножив длину на ширину. Это следует из теоремы Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В прямоугольнике гипотенуза — это диагональ, а катеты — это длина и ширина.
- Площадь прямоугольника можно также найти, разделив периметр на 4 и умножив на длину или ширину. Это следует из того, что периметр прямоугольника равен сумме длин всех его сторон, а длина и ширина прямоугольника равны.
- Площадь прямоугольника можно также найти, используя формулу S = ab, где S — площадь, a — длина и b — ширина. Эта формула следует из того, что площадь прямоугольника равна произведению его длины и ширины.

Как поступить, если фигура имеет три или четыре вершины?
В первом случае он окажется треугольником, и можно воспользоваться одной из формул:
- S = 1/2 * а * н, где а — сторона, н — высота к ней;
- S = 1/2 * а * в * sin (А), где а, в — сторон\ы треугольника, А — угол между известными сторонами;
- S = √(p * (p — а) * (p — в) * (p — с)), где с — сторона треугольника, к уже обозначенным двум, р — полупериметр, то есть сумма всех трех сторон, разделенная на два.
Поэтому это значение может быть получено только бесконечным процессом перехода к пределу. С древности эта проблема привлекла внимание ученых; прежде всего, изобретательный метод, позволяющий верхним архимедам вычислять площадь нескольких фигур, не может быть отключен.
Чтобы определить площадь фигуры, окруженной кривой, Архимед начал вычитать фигуру из многоугольника внутри нее, из которого вы могли бы легко вычислить площадь. Из оставшейся фигуры он вычитал все более тонкие полигоны, пока фигура не исчерпалась; добавив области выгравированных многоугольников, по умолчанию всегда было найдено приблизительное значение искомой области, точное значение которой было задано пределом последовательности этих значений. С помощью метода исчерпания Архимед мог вычислить площадь круга, параболический и т.д. а также несколько томов.
Фигура с четырьмя вершинами может оказаться параллелограммом:
- S = а * н;
- S = 1/2 * d 1 * d 2 * sin(α), где d 1 и d 2 — диагонали, α — угол между ними;
- S = a * в * sin(α).
Формула для площади трапеции: S = н * (a + в) / 2, где а и в — длины оснований.
Опыт других людей
Площадь многоугольника можно найти различными способами, в том числе и с использованием формулы для прямоугольника. Многие люди отмечают, что теорема о площади прямоугольника является простым и эффективным способом нахождения площади многоугольника. Они отмечают, что благодаря этой теореме они могут легко и быстро рассчитать площадь любого прямоугольного многоугольника. Кроме того, многие высказывают мнение, что знание этой теоремы помогает им лучше понимать геометрические свойства фигур и применять их на практике.

Как поступить с правильным многоугольником, у которого больше четырех вершин?
Для начала такая фигура характеризуется тем, что в ней все стороны равны. Плюс к этому, у многоугольника одинаковые углы.
Из метода истощения древних мы перешли к самым
современным методам
интегрального исчисления, которые, хотя и более общие, всегда дают искомую область как предел бесконечных приближенных значений. Сумма прямоугольных областей, которые также содержат только несколько точек внутри кривой, вместо этого будет областью другой «многоугольной» формы, содержащей полную кривую данных и, следовательно, больше, чем искомая область, так что получаются два приблизительных значения, один за другим, другой — избытком, области, окруженной кривой.
Разница между ними и, следовательно, ошибка, которая ниже, будет такой же малой, как и меньшие стороны прямоугольников, поскольку эта разница это не что иное, как площадь всех прямоугольников, которые содержат некоторую точку контура. Этот предел обозначается символом. Таким образом, при расчете площади А, заключенной в три прямых сегмента, две перпендикулярные третьей в концах и кривая, соединяющая свободные крайности двух, она может действовать аналогичным образом, разделяя площадь то же самое во многих строках через параллельные линии для двух сегментов.
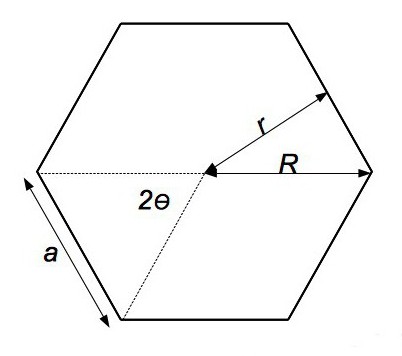
Если вокруг такой фигуры описать окружность, то ее радиус совпадет с отрезком от центра многоугольника до одной из вершин. Поэтому для того чтобы вычислить площадь
правильного многоугольника
с произвольным числом вершин, потребуется такая формула:
S n = 1/2 * n * R n 2 * sin (360º/n), где n — количество вершин многоугольника.
Площадь каждого из них будет больше, чем максимальный прямоугольник, указанный в нем, и меньше минимального описанного прямоугольника, поэтому область поиска будет состоять из области всех зарегистрированных прямоугольников и всех описанных прямоугольников.
Однако из вышесказанного следует отметить, что понятие интегрального интеграла функции берет свое начало из интуитивной области области, на самом деле это не что иное, как пояснение и аналитическое определение. Это понятие очень важно в теории
географических карт
. При интегральном вычислении можно определить и вычислить, в некоторых случаях, также область областей, простирающихся до бесконечности. Итак, с. например, обнаружено, что площадь между циссоидом и его асимптотой в 3 раза больше площади окружности, из которой исходит кривая.
Из нее легко получить такую, которая пригодится для частных случаев:
- треугольника: S = (3√3)/4 * R 2 ;
- квадрата: S = 2 * R 2 ;
- шестиугольника: S = (3√3)/2 * R 2 .
Ситуация с неправильной фигурой
Выходом для того, как узнать площадь многоугольника, если он не является правильным и его нельзя отнести ни к одной из известных ранее фигур, является алгоритм:
Существуют также различные механические инструменты, называемые планиметрами для расчета площади, заключенной в кривую: описывая кривую кончиком устройства, это немедленно обеспечивает искомую область. Параболический сектор. Ограниченной области параллелограмма с одной стороны на струне.
Изогнутая площадь поверхности. — Для определения и расчета криволинейной поверхности возникают еще более сложные проблемы, чем в предыдущих случаях, но при интегральном вычислении мы можем добиться выражения области, не имеющей интуитивной концепции, которую мы все имеем Между тем, в простейшем случае рассматриваемая поверхность может опираться на плоскость без шлака или складчатости, т.е. она может быть разработана, как сказано в более точных терминах, проблема вернется к предыдущему случаю. для релаксации в плоской области, ограниченной определенным контуром, и ее площадь будет вычислимой с уже обработанными процессами.
- разбить его на
простые фигуры
, например, треугольники, чтобы они не пересекались; - вычислить их площади по любой формуле;
- сложить все результаты.
Что делать, если в задаче даны координаты вершин многоугольника?
То есть известен набор пар чисел для каждой точки, которые ограничивают стороны фигуры. Обычно они записываются как (x 1 ; y 1) для первой, (x 2 ; y 2) — для второй, а n-ая вершина имеет такие значения (x n ; y n). Тогда площадь многоугольника определяется, как сумма n слагаемых. Каждое из них выглядит так: ((y i+1 +y i)/2) * (x i+1 — x i). В этом выражении i изменяется от единицы до n.
Таким образом, например, в случае цилиндрической или конической поверхности достаточно разрезать поверхность вдоль генератора, а затем распространить его на самолете. Таким образом, с. например, в случае сферы, в соответствии с методом Архимеда, мы можем представить себе, чтобы заключить сам шар внутри твердого тела образуется так много полос касательной к параллельной системе, а затем рассчитать общую площадь всех этих полос развертывающихся.
Задание «область даст приближенное значение» искомой области;. и будет более приближена столько, сколько полоски плотно и тонкий предел последовательности более приближенных значений, полученных с учетом полосы неопределенно долго уменьшающуюся ширину, то это будет точное значение поиск области. Другой способ для определения изогнутой поверхности была предложена на рассмотрение многогранной поверхности, записанной в одной и той же поверхности.
Стоит отметить, что знак результата будет зависеть от обхода фигуры. При использовании указанной формулы и движении по часовой стрелке ответ будет получаться отрицательным.
Пример задачи
Условие. Координаты вершин заданы такими значениями (0.6; 2.1), (1.8; 3.6), (2.2; 2.3), (3.6; 2.4), (3.1; 0.5). Требуется вычислить площадь многоугольника.
Другой способ определения область, таким образом, хорошо реагирующим на интуитивной концепции, является то, что дается Минковский. Эта математическая воображает трек, с центром в каждой данной точке поверхности, многие сферы радиусом, равным, очень мало. Это будет более приближено чем меньший диаметр, предельное значение этого отношения объема слоя для диаметра шариков, когда диаметр олицетворяет собой бесконечно, он даст точное значение искомой области. Более того, даже сегодня обсуждались на протяжении многих математиков о том, как лучше всего определить именно понятие площади поверхности таким образом, подходит для интуитивной идеи, что все мы имеем.
Решение. По формуле, указанной выше, первое слагаемое будет равно (1.8 + 0.6)/2 * (3.6 — 2.1). Здесь нужно просто взять значения для игрека и икса от второй и первой точек. Несложный расчет приведет к результату 1.8.
Второе слагаемое аналогично получается: (2.2 + 1.8)/2 * (2.3 — 3.6) = -2.6. При решении подобных задач не стоит пугаться отрицательных величин. Все идет так, как нужно. Это планомерно.
Наконец, мы не можем игнорировать тот факт, что проблема определения замкнутой кривой длины и включения максимальной площади была отправной точкой процветающей ветви современной математики, т.е. расчета вариаций. Правый круговой цилиндр. Круглый круговой конус.
Принцип областей. — Второй закон Кеплера утверждает, что области, описываемые плоскими лучами, пропорциональны временам их описания. Это частный случай
общего принципа
, который берет название принципа областей или моментов количества движения. Тогда будет следующее соотношение. В этом случае из предыдущей формулы вытекает, что величина движения поля постоянна. В частности, следует, что если система не подвержена какой-либо внешней силе, ее величина движения поля находится в любой точке постоянной.
Подобным образом получаются значения для третьего (0.29), четвертого (-6.365) и пятого слагаемых (2.96). Тогда итоговая площадь равна: 1.8 + (-2.6) + 0.29 + (-6.365) + 2.96 = — 3.915.
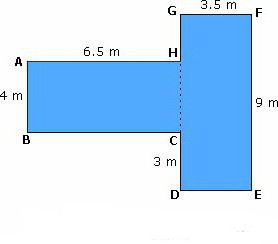
Совет по решению задачи, для которой многоугольник изображен на бумаге в клетку
Чаще всего озадачивает то, что в данных имеется только размер клеточки. Но оказывается, что больше сведений не нужно. Рекомендацией к решению такой задачи является разбивание фигуры на множество треугольников и прямоугольников. Их площади довольно просто сосчитать по длинам сторон, которые потом легко сложить.
По этой причине объем полевого движения планеты постоянный относительно Солнца, когда пренебрегают возмущением других планет. Второй закон Кеплера выражает это свойство. Латинцы с областью слова указали свободное пространство с плоским пространством, имеющее
квадратные функции
. Эти места обычно освящались некоторым богам, и в этом случае они были украшены алтарями, расположенными в центре, или колоннами, статуями и т.д.
Чтобы защитить эти районы и указать их пределы частным зданиям, он также использовался, чтобы забрать их с забором или стенами. Площадь также была объявлена незакрытым пространством, оставленным на переднем плане дома или в общественном здании. Даже так называлось свободное основание кладбища, по периметру которого находились могилы. В центре находился пирс, на котором были сожжены трупы.
Но часто есть более простой подход. Он заключается в том, чтобы дорисовать фигуру до прямоугольника и вычислить значение его площади. Потом сосчитать площади тех элементов, которые оказались лишними. Вычесть их из
общего значения
. Этот вариант порой предполагает несколько меньшее число действий.
Площадь, одна из основных величин, связанных с
геометрическими фигурами
. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П. было уже в древности… …
У этого термина существуют и другие значения, см. Площадь (значения). Площадь плоской фигуры аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное… … Википедия
I Площадь одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П.… …
Большая советская энциклопедия
У этого термина существуют и другие значения, см. Площадь (значения). Площадь Размерность L² Единицы измерения СИ м² … Википедия
Ж. 1. Часть земной поверхности, пространство, естественно ограниченное или специально выделенное для какой либо цели. отт. Водное пространство. отт. Большое, ровное место, пространство. 2. Ровное незастроенное пространство общественного… …
Современный
толковый словарь
русского языка Ефремовой
Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/2 сентября 2012. Пока процесс обсуждения не завершён, статью можно попытаться улучшить, однако следует… … Википедия
Две фигуры в R2, имеющие
равные площади
и соответственно два многоугольника M1 и М 2 такие, что их можно разрезать на многоугольники так, что части, составляющие М 1, соответственно конгруэнтны частям, составляющим М 2. Для, равновеликость… …
Математическая энциклопедия
В=7, Г=8, В + Г/2 − 1= 10 Теорема Пика классический результат комбинаторной геометрии и геометрии чисел. Площадь многоугольника с целочисле … Википедия
У этого термина существуют и другие значения, см. Теорема Пика. В = 7, Г = 8, В + Г/2 − 1 = 10 Формула Пика (или теорема Пика) классический результат комбинаторной геометрии и геометрии чисел. Площадь … Википедия
Область (связное открытое множество) на границе выпуклого тела в евклидовом пространстве Е 3. Вся граница выпуклого тела наз. полной В. п. Если тело конечно, то полная В. п. наз. замкнутой. Если тело бесконечно, то полная В. п. наз. бесконечной.… …
Математическая энциклопедия
Возможно, будет полезно почитать:
- Тюменское высшее военно-инженерное командное училище имени маршала инженерных войск А
; - Почему ссср ввязался в гражданскую войну в испании Испанская гражданская война 1936 1939 кратко
; - Савинов, Пётр Иванович: биография Капитан вов савинов п и танкист ас
; - Методы решения неопределенных интегралов
; - Основные проблемы, изучаемые на макроэкономическом уровне
; - Свинья скорпион карьера и финансы
; - Как производится расчет пени по налогам: начисление пени, порядок расчета, пример вычислений
; - Дарение полностью самортизированного объекта ОС
;
Частые вопросы
Как найти площадь многоугольника формула?
Ответ: Формула для нахождения площади правильного многоугольника: Площадь = 1/2 * периметр * апофема. * Периметр – сумма сторон многоугольника. * Апофема – отрезок, соединяющий центр многоугольника и середину любой из его сторон. 1.
Что такое площадь многоугольника?
Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник. Измерение площади связано со сравнением занимаемой части плоскости с некими единицами измерения площади.
Как найти площадь прямоугольника двумя способами 3 класс?
Чтобы узнать площадь прямоугольника, можно найти квадрат диагонали и любой стороны, из первого числа вычесть второе, найти корень из результата, и на полученное число умножить длину известной стороны. Вуаля! S = a × √(d2 — а2), где а — известная сторона, d — диагональ.
Как найти площадь прямоугольника в 4 классе?
Известно, что площадь прямоугольника равна произведению длин его сторон: S пр = a ⋅ b .
Полезные советы
СОВЕТ №1
Используйте формулу для нахождения площади прямоугольника: S = a * b, где S — площадь, a и b — длины сторон прямоугольника.
СОВЕТ №2
Если у вас есть многоугольник, который можно разбить на прямоугольники, найдите площадь каждого прямоугольника и сложите их, чтобы получить общую площадь многоугольника.
СОВЕТ №3
Используйте теорему о площади прямоугольника: S = a * b, где S — площадь, a и b — длины сторон прямоугольника, чтобы быстро и легко найти площадь прямоугольных участков многоугольника.