Прежде всего, треугольник – это
геометрическая фигура
, которая образуется тремя, не лежащими на одной прямой, точками, которые соединены тремя отрезками. Чтобы найти, чему равна высота треугольника, необходимо, в первую очередь, определить его тип. Треугольники различаются величиной углов и количеством равных углов. По величине углов треугольник может быть остроугольным, тупоугольным и прямоугольным. По числу равных сторон выделяют равнобедренный, равносторонний и разносторонний треугольники. Высота – это перпендикуляр, который опущен на противоположную сторону треугольника из его вершины. Как найти высоту треугольника?
Как найти высоту равнобедренного треугольника
Для равнобедренного треугольника характерно равенство сторон и углов при его основании, поэтому проведенные к боковым сторонам высоты равнобедренного треугольника всегда равны друг другу. Также высота данного треугольника одновременно является медианой и биссектрисой. Соответственно, высота делит основание пополам. Рассматриваем получившийся прямоугольный треугольник и находим сторону, то есть высоту равнобедренного треугольника, посредством теоремы Пифагора. Воспользовавшись следующей формулой, вычисляем высоту: H = 1/2*√4*a 2 − b 2 , где: а — боковая сторона данного равнобедренного треугольника, b — основание данного равнобедренного треугольника.
Мнение эксперта:
При поиске стороны равностороннего треугольника по известной площади, эксперты рекомендуют использовать следующую формулу: сторона = √(4 * площадь / √3). Это позволяет быстро и точно определить длину стороны треугольника, основываясь исключительно на известной площади. Такой подход особенно полезен при решении задач в геометрии и инженерных расчетах.

Как найти высоту равностороннего треугольника
Треугольник с
равными сторонами
называется равносторонним. Высоту такого треугольника выводят из формулы высоты равнобедренного треугольника. Получается: H = √3/2*a, где a — сторона данного равностороннего треугольника.
Интересные факты
-
Площадь равностороннего треугольника можно найти по формуле: S = (√3/4) * a^2, где a — длина стороны треугольника.
-
Если известна площадь равностороннего треугольника, то длину его стороны можно найти по формуле: a = √(4S / √3).
-
Равносторонний треугольник — это единственный треугольник, у которого все стороны равны и все углы равны 60 градусам.
Как найти высоту разностороннего треугольника
Разносторонним называют треугольник, у которого какие-либо две стороны не являются равными друг другу. В таком треугольнике все три высоты будут разными. Рассчитать длины высот можно при помощи формулы: H = sin60*a = a*(sgrt3)/2, где а — сторона треугольника или сначала посчитать площадь конкретного треугольника по формуле Герона, которая выглядит как: S = (p*(p-c)*(p-b)*(p-a))^1/2, где а, b, с – стороны разностороннего треугольника, а p – его полупериметр. Каждая высота = 2*площадь/сторону
Опыт других людей
Когда речь заходит о поиске стороны равностороннего треугольника, зная только его площадь, люди высказывают разные мнения. Некоторые утверждают, что можно воспользоваться формулой для площади равностороннего треугольника и выразить сторону через нее. Другие считают, что для нахождения стороны требуется дополнительная информация, такая как высота или угол. Все это побуждает задуматься о том, какой метод является наиболее эффективным и точным.

Как найти высоту прямоугольного треугольника
Прямоугольный треугольник имеет один прямой угол. Высота, которая проходит к одному из катетов, в то же время является вторым катетом. Поэтому чтобы найти лежащие на катетах высоты, нужно воспользоваться изменённой формулой Пифагора: a = √(c 2 − b 2), где a, b — это катеты (a — катет, который необходимо найти), c — длина гипотенузы. Для того, чтобы найти вторую высоту надо поставить полученное значение a на место b. Для нахождения третьей, лежащей внутри треугольника, высоты применяется следующая формула: h = 2s/a, где h — высота прямоугольного треугольника, s — его площадь, a — длина стороны, к которой будет перпендикулярна высота.
Треугольник называется остроугольным в случае, если все его углы острые. В таком случае все три высоты располагаются внутри остроугольного треугольника. Треугольник называется тупоугольным при наличии одного тупого угла. Две высоты тупоугольного треугольника находятся вне треугольника и падают на продолжение сторон. Третья сторона находится внутри треугольника. Высота определяется при помощи все той же теоремы Пифагора.
Общие формулы, как вычисления высоты треугольника
- Формула для нахождения высоты треугольника через стороны: H= 2/a √p*(p-c)*(p-b)*(p-b), где h — высота, которую нужно найти, а, b и c – стороны данного треугольника, p – его полупериметр, .
- Формула для нахождения высоты треугольника через угол и сторону: H=b sin y = c sin ß
- Формула для нахождения высоты треугольника через площадь и сторону: h = 2S/a, где a – это сторона треугольника, а h – построенная к стороне а высота.
- Формула для нахождения высоты треугольника через радиус и стороны: H= bc/2R.
Равносторонний треугольник — это треугольник, все стороны которого равны, как следует из его названия. Эта особенность существенно упрощает нахождение остальных параметров треугольника, в том числе его высоты.
Вам понадобится
Длина стороны равностороннего треугольника
Спонсор размещения P&G
Статьи по теме «Как найти высоту равностороннего треугольника»
Как найти высоту в равнобедренном треугольнике
Как найти основание треугольника
Как найти площадь поверхности пирамиды
Инструкция
В равностороннем треугольнике все углы также равны. Угол равностороннего треугольника, отсюда, равен 180/3 = 60 градусов. Очевидно, что так как все стороны и все углы такого треугольника равны, то все его высоты также будут равны.
В равностороннем треугольнике ABC можно провести, например, высоту AE. Так как равносторонний треугольник — это частный случай равнобедренного треугольника, а AB = AC. Следовательно, по свойству равнобедренного треугольника высота AE будет одновременно медианой (то есть BE = EC) треугольника ABC и биссектрисой угла BAC (то есть BAE = CAE).
Высота AE будет являться катетом прямоугольного треугольника BAE с гипотенузой AB. AB = a — длина стороны равностороннего треугольника. Тогда AE = AB*sin(ABE) = a*sin(60o) = sqrt(3)*a/2. Следовательно, для нахождения высоты равностороннего треугольника, достаточно знать только длину его стороны.
Очевидно, что если задана медиана или биссектриса равностороннего треугольника, то она и будет являться его высотой.
Как просто
Другие новости по теме:
Под высотой треугольника понимается отрезок, проведенный перпендикулярно из вершины треугольника к противоположной стороне. Высота треугольника вполне может совпадать со стороной треугольника, если он прямоугольный, а также находиться вне треугольника, если треугольник остроугольный. Расчет длины
Равносторонний треугольник наряду с квадратом является, пожалуй, самой простой и симметричной фигурой в планиметрии. Разумеется, все соотношения, справедливые для обычного треугольника, верны также и для равностороннего. Однако для правильного треугольника все формулы становятся намного проще. Вам
У равнобедренного треугольника две стороны равны, углы при его основании тоже будут равны. Поэтому биссектрисы, проведенные к боковым сторонам, будут равны друг другу. Биссектриса, проведенная к основанию равнобедренного треугольника, будет одновременно медианой и высотой этого треугольника.
У равнобедренного треугольника две стороны равны, углы при его основании тоже равны. Поэтому высоты, проведенные к боковым сторонам, будут равны друг другу. Высота, проведенная к основанию равнобедренного треугольника, будет одновременно медианой и биссектрисой этого треугольника. Спонсор
Медиана — это отрезок, соединяющий вершину треугольника и середину противолежащей стороны. Зная длины всех трех сторон треугольника, можно найти его медианы. В частных случаях равнобедренного и равностороннего треугольника, очевидно, достаточно знания, соответственно, двух (не равных друг другу) и
Равносторонним называют треугольник, имеющий три равные стороны и три одинаковых угла. Такой треугольник еще называют правильным. Высота, проведенная из вершины к основанию, одновременно является биссектрисой и медианой, из чего следует, что эта линия делит угол вершины на два равных угла, а
Как видно на рисунке, равнобедренным является треугольник, две
боковые стороны
которого равны. Найти площадь равнобедренного треугольника можно, зная длину его основания и высоты или по длине его основания и любой боковой стороны треугольника. Вам понадобится — геометрическая формула для нахождения
В равностороннем треугольнике высота h делит фигуру на два одинаковых
прямоугольных треугольника
. В каждом из них h — катет, сторона a — гипотенуза. Можно выразить a через высоту равносторонней фигуры, а потом найти площадь. Спонсор размещения P&G Статьи по теме «Как по высоте в равностороннем
Медиана треугольника — это отрезок, который соединяет вершину треугольника с серединой противоположной стороны. В равностороннем треугольнике медиана является биссектрисой и высотой одновременно. Таким образом, нужный отрезок можно построить несколькими способами. Вам понадобится — карандаш; —
Поиск периметра равностороннего треугольника означает расчет расстояния вокруг самой фигуры. Самый простой способ — это сложить все стороны. Однако бывают случаи, когда известна лишь высота треугольника или одна сторона, как быть в таких ситуациях? Статья подскажет, как быстро находить периметр треугольника при разных условиях.
Равносторонний треугольник – что собой представляет
Такой треугольник имеет три конгруэнтные стороны и три равных угла. Зная размер одной из сторон, можно найти остальные. Поскольку треугольник имеет три соразмерные стороны, он автоматически имеет три идентичных угла. Они в сумме дают 180º, которую, согласно их идентичности, следует разделить на 3. Это означает, что любой угол треугольника равен 60 º. Можно сделать заключение, что равносторонний треугольник является острой фигурой.
Как найти периметр равностороннего треугольника
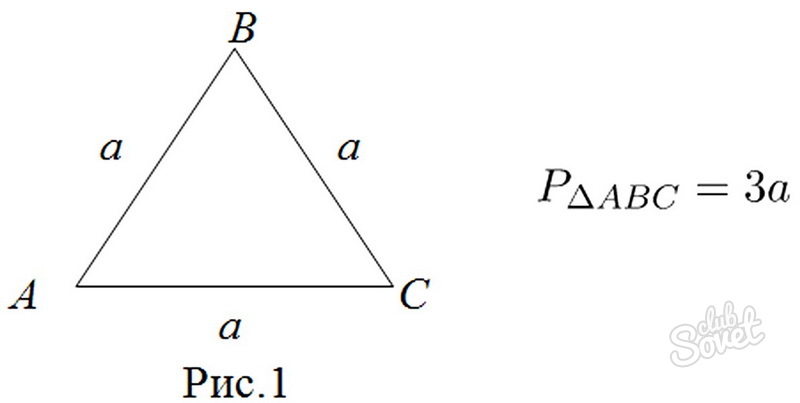
Поскольку стороны равностороннего треугольника конгруэнтны, для вычисления его периметра требуется длина одной стороны. Можно сказать, что простая формула периметра равносторонней фигуры: Р = c+c+c, где с – длина одной из сторон.
- Узнайте периметр треугольника с конгруэнтными сторонами, если размер одной — 7 дм.
- Из условия известно, что сторона фигуры 7 дм, т.е. другие стороны идентичны.
- Согласно формулы периметр треугольника: Р = с + с + с, Р = 7+7+7 = 21 дм.
Упрощенный способ нахождения периметра равностороннего треугольника
Конечно, более простой способ найти границы треугольника — это умножить длину каждой стороны на три. Формула будет состоять: P = 3 х а, где а — длина стороны.
- Оцените периметр равностороннего треугольника с заданной стороной 7 дм.
- Подставьте значения согласно формулы:
P= 3 х а
,
P= 3 х 7
P= 21 - Периметр треугольника составляет 21 дм.
- Когда изначально стороны треугольника заданы в сантиметрах, ваш ответ также должен быть в сантиметрах. В приведенном примере длина сторон составляет 7 дм, поэтому
правильное значение
периметра будет 21 дм.
Как найти периметр равностороннего треугольника через высоту
- Высота треугольника с равными сторонами 7 см, найдите периметр.
- Согласно условия h = 7 см, следуя формуле:
- Р= 2√3 х 7 = 24,249 см.
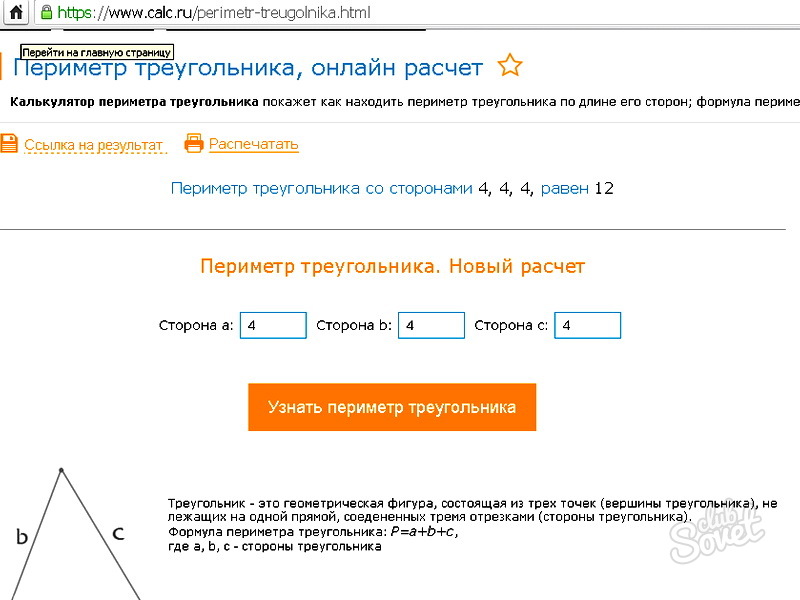
Онлайн расчет периметра равностороннего треугольника
Существует несколько сайтов (например, справочный портал Калькулятор или познавательный портал 2mb), которые помогут быстро рассчитать периметр треугольника, достаточно лишь ввести его параметры.
Как найти периметр равностороннего треугольника — обратный расчет
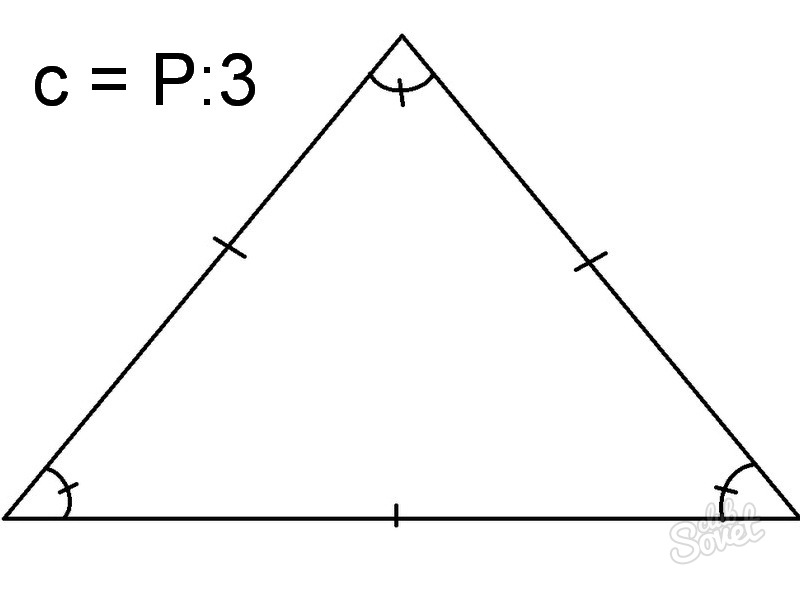
Бывают случаи, когда в школе требуется найти сторону равностороннего треугольника, когда в условии указан периметр фигуры. Примените полученные знания: Р = 3 х с, значит с = Р: 3
- Найдите длину стороны равностороннего треугольника, когда периметр 24 см.
- Исходя из формулы: с = Р: 3, с = 24: 3 = 8 см
- Длина сторон заданного треугольника 8 см.
Нахождение периметра равностороннего треугольника не составит труда, если правильно применять основные формулы расчета.
Возможно, будет полезно почитать:
- Дельвиг, Антон Антонович – краткая биография
; - Афанасий никитин, русский путешественник
; - Мария Волконская Сообщение о волконской марии николаевне кратко
; - Краткая биография рембрандта и его творчество
; - Эдуард ii плантагенет, король англии
; - Белецкий — значение и происхождение фамилии Руководствовался «флюидами неприязни»
; - Восточный гороскоп Какое сегодня год по японскому летоисчислению
; - Вредна ли шаурма Вредна ли шаурма для желудка
;
Частые вопросы
Как найти сторону треугольника если известна его площадь?
Площадь треугольника можно определить как половину произведения длины стороны треугольника на длину высоты, проведенную к этой стороне: S = a * h / 2. Следовательно, зная высоту и площадь треугольника, можно найти сторону: a = 2 * S / h = 2 * 18 / 9 = 4 см.
Как найти периметр равностороннего треугольника зная его площадь?
Как найти периметр треугольника, зная его площадь и радиус вписанной окружности Умножьте площадь треугольника на 2. Разделите результат на радиус вписанной окружности.
Как найти третью сторону треугольника и его площадь?
Для нахождения третьей стороны треугольника по известным сторонам и углу между ними, можно использовать теорему косинусов. Формула для нахождения третьей стороны выглядит следующим образом: c^2 = a^2 + b^2 — 2ab*cos(C), где c — третья сторона, a и b — известные стороны, C — угол между этими сторонами.
Как найти площадь равностороннего треугольника зная сторону?
Да, для нахождения площади правильного треугольника с известной длиной одной его стороны существует формула: Площадь = (сторона^2 * √3) / 4. В данной формуле сторона — известное значение длины одной из сторон треугольника.
Полезные советы
СОВЕТ №1
Используйте формулу для нахождения стороны равностороннего треугольника: a = √(4S/√3), где a — сторона треугольника, S — площадь треугольника.
СОВЕТ №2
Проверьте правильность вычислений, чтобы избежать ошибок при нахождении стороны равностороннего треугольника.