«Квадратичная функция» — Свойства: -Промежутки монотонности при а > 0 при а
«Степенная функция 9 класс» — Нам знакомы функции. Степенная функция. У. 0. 9 класс учитель Ладошкина И.А. У = х2, у = х4 , у = х6, у = х8, … Показатель – четное натуральное число (2n). У = х. Парабола. Кубическая парабола. Функция у=х2n четная, т.к. (–х)2n = х2n.
«8 класс квадратичная функция» — 1) Построить вершину параболы. -1. Построить график функции. 2) Построить ось симметрии x=-1. y. Алгебра 8 класс Учитель 496 школы Бовина Т. В. Построение графика квадратичной функции. x. -7. План построения.
«График функции Y X» — Графиком функции y=x2 + п является парабола с вершиной в точке (0; п). График функции y=(x — m)2 является параболой с вершиной в точке (m; 0). Чтобы увидеть графики, щелкни мышкой. Страница отображается по щелчку. Из выше сказанного следует, что графиком функции y=(x — m)2 + п является парабола с вершиной в точке (m; п).
«Натуральный логарифм» — 0,1. «Логарифмический дартс». 0,04. 121. Натуральные логарифмы. 7. 4.
«Квадратичная функция и её график» — Автор: Гранов Илья. Решение задач: Решение.у=4x А(0,5:1) 1=1 А-принадлежит. 4.ли графику функции y=4x точка: А(0,5:1) В(-1:-4)С(-2:16)D(0,1:0,4)? При а=1 формула у=аx принимает вид.
Всего в теме
25 презентаций
Математика выделилась из общей философии примерно в шестом веке до н. э., и с этого момента началось ее победное шествие по миру. Каждый этап развития вносил что-то новое — элементарный счет эволюционировал, преображался в дифференциальное и интегральное исчисление, сменялись века, формулы становились все запутаннее, и настал тот момент, когда «началась самая сложная математика — из нее исчезли все числа». Но что же лежало в основе?
Начало начал
Натуральные числа
появились наравне с первыми математическими операциями. Раз корешок, два корешок, три корешок… Появились они благодаря индийским ученым, которые вывели первую позиционную
Слово «позиционность» означает, что расположение каждой цифры в числе строго определено и соответствует своему разряду. Например, числа 784 и 487 — цифры одни и те же, но числа не являются равносильными, так как первое включает в себя 7 сотен, тогда как второе — только 4. Нововведение индийцев подхватили арабы, которые довели числа до того вида, который мы знаем сейчас.
В древности числам придавалось
мистическое значение
, Пифагор полагал, что число лежит в основе сотворения мира наравне с основными стихиями — огнем, водой, землей, воздухом. Если рассматривать все лишь с математической стороны, то что такое натуральное число? Поле натуральных чисел обозначается как N и представляет собой бесконечный ряд из чисел, которые являются целыми и положительными: 1, 2, 3, … + ∞. Ноль исключается. Используется в основном для подсчета предметов и указания порядка.
Мнение эксперта:
Эксперты отмечают, что каждое натуральное число представляет собой уникальную комбинацию простых чисел. Это означает, что каждое натуральное число можно представить в виде произведения простых множителей. Например, число 12 можно представить как 2*2*3, а число 30 — как 2*3*5. Этот принцип является основой для теории чисел и играет важную роль в математике и криптографии. Понимание того, как получается каждое натуральное число, помогает углубить знания о структуре чисел и их взаимосвязях, что в свою очередь имеет практическое применение в различных областях науки и техники.

Что такое в математике? Аксиомы Пеано
Поле N является базовым, на которое опирается элементарная математика. С течением времени выделяли поля целых, рациональных,
Работы итальянского математика Джузеппе Пеано сделали возможной дальнейшую структуризацию арифметики, добились ее формальности и подготовили почву для дальнейших выводов, которые выходили за рамки области поля N.
Что такое натуральное число, было выяснено ранее
простым языком
, ниже будет рассмотрено математическое определение на базе аксиом Пеано.
- Единица считается натуральным числом.
- Число, которое идет за натуральным числом, является натуральным.
- Перед единицей нет никакого натурального числа.
- Если число b следует как за числом c, так и за числом d, то c=d.
- Аксиома индукции, которая в свою очередь показывает, что такое натуральное число: если некоторое утверждение, которое зависит от параметра, верно для числа 1, то положим, что оно работает и для числа n из поля натуральных чисел N. Тогда утверждение верно и для n=1 из поля натуральных чисел N.
Интересные факты
- Каждое натуральное число можно представить в виде суммы последовательных натуральных чисел. Например, 10 = 1 + 2 + 3 + 4. Это свойство называется принципом математической индукции и используется для доказательства многих теорем в математике.
- Натуральные числа можно разделить на четные и нечетные. Четные числа делятся на два без остатка, а нечетные числа не делятся на два без остатка. Сумма двух четных чисел всегда четное число, а сумма двух нечетных чисел всегда нечетное число.
- Натуральные числа можно использовать для счета предметов. Например, если у вас есть 10 яблок, вы можете сосчитать их, сказав: «Один, два, три, четыре, пять, шесть, семь, восемь, девять, десять». Счет предметов с помощью натуральных чисел позволяет нам сравнивать количество предметов и определять, какой набор предметов больше, а какой меньше.

Основные операции для поля натуральных чисел
Так как поле N стало первым для математических расчетов, то именно к нему относятся как области определения, так и области значений ряда операций ниже. Они бывают замкнутыми и нет. Основным различием является то, что замкнутые операции гарантированно оставляют результат в рамках множества N вне зависимости от того, какие числа задействованы. Достаточно того, что они натуральные. Исход остальных численных взаимодействий уже не столь однозначен и напрямую зависит от того, что за числа участвуют в выражении, так как он может противоречить основному определению. Итак, замкнутые операции:
- сложение — x + y = z, где x, y, z включены в поле N;
- умножение — x * y = z, где x, y, z включены в поле N;
- возведение в степень — x y , где x, y включены в поле N.
Остальные операции, итог которых может не существовать в контексте определения «что такое натуральное число», следующие:
Опыт других людей
Каждое натуральное число уникально и вызывает интерес у многих. Люди говорят, что процесс получения каждого натурального числа удивителен и загадочен. Некоторые утверждают, что это связано с математическими закономерностями, другие считают, что это результат бесконечной последовательности чисел. Натуральные числа поражают своей разнообразием и бесконечностью, оставляя людей в восторге от их неисчерпаемой природы.

Свойства чисел, принадлежащих полю N
Все дальнейшие математические рассуждения будут основываться на следующих свойствах, самых тривиальных, но от этого не менее важных.
- Переместительное свойство сложения — x + y = y + x, где числа x, y включены в поле N. Или всем известное «от перемены мест слагаемых сумма не меняется».
- Переместительное свойство умножения — x * y = y * x, где числа x, y включены в поле N.
- Сочетательное свойство сложения — (x + y) + z = x + (y + z), где x, y, z включены в поле N.
- Сочетательное свойство умножения — (x * y) * z = x * (y * z), где числа x, y, z включены в поле N.
- распределительное свойство — x (y + z) = x * y + x * z, где числа x, y, z включены в поле N.
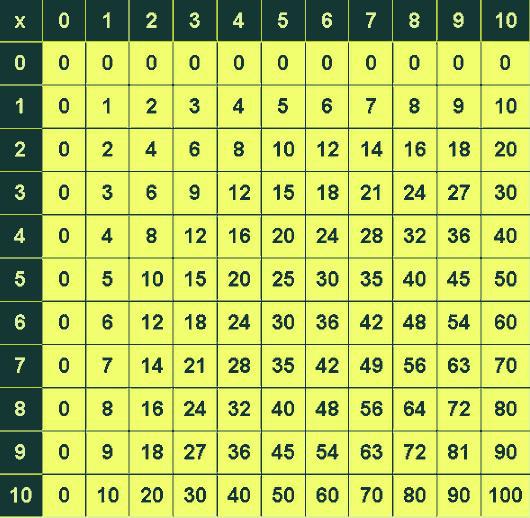
Таблица Пифагора
Одним из первых шагов в познании школьниками всей структуры элементарной математики после того, как они уяснили для себя, какие числа называются натуральными, является таблица Пифагора. Ее можно рассматривать не только с точки зрения науки, но и как ценнейший научный памятник.
Данная таблица умножения претерпела с течением времени ряд изменений: из нее убрали ноль, а числа от 1 до 10 обозначают сами себя, без учета порядков (сотни, тысячи…). Она представляет собой таблицу, в которой заглавия строк и столбцов — числа, а содержимое ячеек их пересечения равно их же произведению.
В практике обучения последних десятилетий наблюдалась необходимость заучивания таблицы Пифагора «по порядку», то есть сначала шло зазубривание. Умножение на 1 исключалось, так как результат был равен 1 или большему множителю. Между тем в таблице невооруженным взглядом можно заметить закономерность: произведение чисел растет на один шаг, который равен заглавию строки. Таким образом, второй множитель показывает нам, сколько раз нужно взять первый, дабы получить искомое произведение. Данная система не в пример удобнее той, что практиковалась в средние века: даже понимая, что такое натуральное число и насколько оно тривиально, люди умудрялись осложнять себе повседневный счет, пользуясь системой, которая базировалась на степенях двойки.
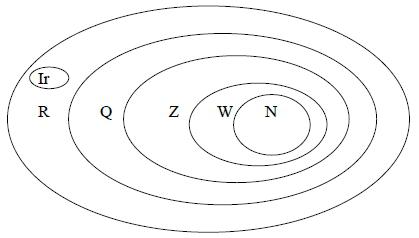
Подмножество как колыбель математики
На
данный момент
поле натуральных чисел N рассматривается лишь как одно из подмножеств комплексных чисел, но это не делает их менее ценными в науке. Натуральное число — первое, что познает ребенок, изучая себя и
окружающий мир
. Раз пальчик, два пальчик… Благодаря ему у человека формируется
логическое мышление
, а также умение определять причину и выводить следствие, подготавливая почву для больших открытий.
Простейшее число — это
натуральное число. Их используют в
повседневной жизни
для подсчета
предметов, т.е. для вычисления их количества и порядка.
Что такое натуральное число:
натуральными числаминазывают числа, которые используются для
подсчета предметов либо для указывания порядкового номера любого предмета из всех однородных
предметов.
Натуральные числа— это числа, начиная с единицы. Они образуются естественным образом при счёте.
Например, 1,2,3,4,5… —первые натуральные числа.
Наименьшее натуральное число— один. Наибольшего натурального числа не существует. При счёте число
ноль не используют, поэтому ноль натуральное число.
Натуральный ряд чисел— это последовательность всех натуральных чисел. Запись натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
В натуральном ряду каждое число больше предыдущего на единицу.
Сколько чисел в натуральном ряду? Натуральный ряд бесконечен, самого большого натурального числа не существует.
Десятичной так как 10 единиц всякого разряда образуют 1 единицу старшего разряда. Позиционной так
как значение цифры зависит от её места в числе, т.е. от разряда, где она записана.
Классы натуральных чисел.
Всякое натуральное число возможно написать при помощи 10-ти арабских цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Для чтения натуральных чисел их разбивают, начиная справа, на группы по 3 цифры в каждой. 3 первые
цифры справа — это класс единиц, 3 следующие — это класс тысяч, далее классы миллионов, миллиардов и
так далее. Каждая из цифр класса называется его
разрядом.
Сравнение натуральных чисел.
Из 2-х натуральных чисел меньше то число, которое при счете называется ранее.
Например, число
7меньше
11(записывают так:
7 ). Когда одно число
больше второго
, это записывают так:
386 > 99.
Таблица разрядов и классов чисел.
|
1-й класс единицы |
1-й разряд единицы 2-й разряд десятки 3-й разряд сотни |
|
2-й класс тысячи |
1-й разряд единицы тысяч 2-й разряд десятки тысяч 3-й разряд сотни тысяч |
|
3-й класс миллионы |
1-й разряд единицы миллионов 2-й разряд десятки миллионов 3-й разряд сотни миллионов |
|
4-й класс миллиарды |
1-й разряд единицы миллиардов 2-й разряд десятки миллиардов 3-й разряд сотни миллиардов |
|
Числа от 5-го класса и выше относятся к Основные свойства натуральных чисел.
Действия над натуральными числами. 4. Деление натуральных чисел — операция, обратная операции умножения. Если Формулы для деления: а: 1 = a a: a = 1, a ≠ 0 0: a = 0, a ≠ 0
(
( Числовые выражения и числовые равенства. Запись, где числа соединяются знаками действий, является Например, 10∙3+4; (60-2∙5):10. Записи, где знаком равенства объединены 2 числовых выражения, является Порядок выполнения арифметических действий. Сложение и вычитание чисел — это действия первой степени, а умножение и деление — это действия второй степени. Когда числовое выражение состоит из действий только одной степени, то их выполняют последовательно Когда выражения состоят из действия только первой и второй степени, то сначала выполняют действия Когда в выражении есть скобки — сначала выполняют действия в скобках. Например, 36:(10-4)+3∙5= 36:6+15 = 6+15 = 21. |
Возможно, будет полезно почитать:
- Отливка воском: обозначения фигур и их расшифровка
; - Став «кнут» Рунный став огненный кнут com
; - Руны халявы и исполнения желания Рун ставы халява
; - Проверенные руны для исполнения желаний Руны халява которые работают у женщин
; - Рунические формулы на восстановление любовных отношений
; - Что такое крадник и как воспользоваться таким колдовством себе на благо Как забрать красоту и грацию
; - Формулы рун для подключение к денежному эгрегору — Чистка финансового канала Правила проведения обряда
; - Соте из баклажанов на зиму
;
Частые вопросы
Как понять натуральные числа или нет?
Натура́льные чи́сла (от лат. naturalis «естественный») — числа, возникающие естественным образом при счёте (1, 2, 3, 4, 5, 6, 7 и так далее). Последовательность всех натуральных чисел, расположенных в порядке возрастания, называется натуральным рядом.
Почему число 0 не является натуральным числом?
Что такое натуральное число То есть, натуральное число — это число, которое получается естественным образом при подсчёте чего-либо. Ноль не является натуральным числом, ведь ноль — это пустота, нисколько предметов.
Как появились натуральные числа?
Натуральное число — одно из основных понятий математики, позволяющее выразить результаты измерений или счёта. Первые числа возникли очень давно. Это были зарубки на костях, черточки на деревьях. Но большие числа изображать таким образом было неудобно, и в результате появились цифры.
Как называются цифры от 1 до 9?
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого. Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д. Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания.
Полезные советы
СОВЕТ №1
Изучите основные свойства натуральных чисел, такие как ассоциативность, коммутативность, дистрибутивность и т. д. Это поможет вам лучше понять, как каждое натуральное число формируется из более простых элементов.
СОВЕТ №2
Изучите различные методы построения натуральных чисел, такие как метод индукции, метод математической индукции, методы доказательства и т. д. Это поможет вам понять процесс формирования каждого натурального числа.