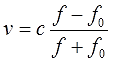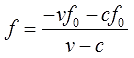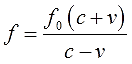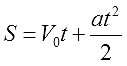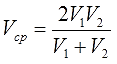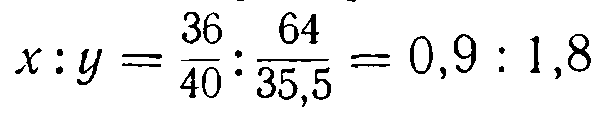Воспользовавшись записью первого начала термодинамики в дифференциальной форме (9.2), получим выражение для теплоёмкости произвольного процесса:
Представим полный дифференциал внутренней энергии через частные производные по параметрам и :
После чего формулу (9.6) перепишем в виде
Соотношение (9.7) имеет самостоятельное значение, поскольку определяет теплоёмкость в любом термодинамическом процессе и для любой макроскопической системы, если известны калорическое и термическое уравнения состояния.
Рассмотрим процесс при постоянном давлении и получим общее соотношение между и .
Исходя из полученной формулы, можно легко найти связь между теплоемкостями и в идеальном газе. Этим мы и займемся. Впрочем, ответ уже известен, мы его активно использовали в 7.5.
Уравнение Роберта Майера
Выразим частные производные в правой части уравнения (9.8), с помощью термического и калорического уравнений, записанных для одного моля идеального газа.
Внутренняя энергия
идеального газа зависит только от температуры и не зависит от объёма газа, следовательно
Из термического уравнения легко получить
Подставим (9.9) и (9.10) в (9.8), тогда
Окончательно запишем
Вы, надеюсь, узнали (9.11). Да, конечно, это уравнение Майера. Еще раз напомним, что уравнение Майера справедливо только для идеального газа.
9.3. Политропические процессы в идеальном газе
Как отмечалось выше первое начало термодинамики можно использовать для вывода уравнений процессов, происходящих в газе. Большое практическое применение находит класс процессов, называемых политропическими.
Политропическим
называется процесс, проходящий при постоянной теплоемкости
.
Уравнение процесса задается функциональной связью двух макроскопических параметров, описывающих систему. На соответствующей координатной плоскости уравнение процесса наглядно представляется в виде графика — кривой процесса. Кривая, изображающая политропический процесс, называется политропой. Уравнение политропического процесса для любого вещества может быть получено на основе первого начала термодинамики с использованием его термического и калорического уравнений состояния. Продемонстрируем, как это делается на примере вывода уравнения процесса для идеального газа.
Вывод уравнения политропического процесса в идеальном газе
Требование постоянства теплоёмкости в процессе позволяет записать первое начало термодинамики в виде
Используя уравнение Майера (9.11) и уравнение состояния идеального газа, получаем следующее выражение для
Разделив уравнение (9.12) на T и подставив в него (9.13) придем к выражению
Разделив () на , находим
Интегрированием (9.15), получаем
Это уравнение политропы в переменных
Исключая из уравнения () , с помощью равенства получаем уравнение политропы в переменных
Параметр называется показателем политропы, который может принимать согласно () самые
разные значения
, положительные и отрицательные, целые и дробные. За формулой () скрывается множество процессов. Известные вам изобарный, изохорный и изотермический процессы являются частными случаями политропического.
К этому классу процессов относится также
адиабатный или адиабатический процесс
. Адиабатным называется процесс, проходящий без теплообмена (). Реализовать такой процесс можно двумя способами. Первый способ предполагает наличие у системы теплоизолирующей оболочки, способной изменять свой объем. Второй – заключается в осуществлении столь быстрого процесса, при котором система не успевает обмениваться количеством теплоты с
окружающей средой
. Процесс распространения звука в газе можно считать адиабатным благодаря его большой скорости.
Из определения теплоемкости следует, что в адиабатическом процессе . Согласно
где – показатель адиабаты.
В этом случае уравнение политропы принимает вид
Уравнение адиабатного процесса (9.20) называют также уравнением Пуассона, поэтому параметр часто именуют постоянной Пуассона. Постоянная является
важной характеристикой
газов. Из опыта следует, что ее значения для разных газов лежат в интервале 1,30 ÷ 1,67, поэтому на диаграмме процессов адиабата «падает» более круто, чем изотерма.
Графики политропических процессов для
различных значений
представлены на рис. 9.1.
На рис. 9.1 графики процессов пронумерованы в соответствии с табл. 9.1.
Этот урок – полезное дополнение к предыдущей теме » «.
Умение делать такие вещи – штука не просто полезная, она –
необходимая. Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях – как базовом, так и профильном.
Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.
Удивляемся, но запоминаем:
Любое равенство с буквами, любая формула – это ТОЖЕ УРАВНЕНИЕ!
А где уравнение, там автоматически и . Вот и применяем их в удобном нам порядке и – готово дело.) Читали предыдущий урок? Нет? Однако… Тогда эта ссылочка – для вас.
Ах, вы в курсе? Отлично! Тогда применяем
теоретические знания
на практике.
Начнём с простого.
Как выразить одну переменную через другую?
Такая задача постоянно возникает при решении
систем уравнений.Например, имеется равенство:
3
x—
2
y
= 5
Здесь
две переменные– икс и игрек.
Допустим, нас просят
выразить
x
через
y.
Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс. В гордом одиночестве, безо всяких соседей и коэффициентов. А справа – что уж получится.
И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном
нампорядке, шаг за шагом добираясь до чистого икса.
Анализируем левую часть уравнения:
3
x
– 2
y
= 5
Здесь нам мешаются тройка перед иксом и —
2
y. Начнём с —
2у, это попроще будет.
Перекидываем —
2уиз левой части в правую. Меняя минус на плюс, разумеется. Т.е. применяем
первоетождественное преобразование:
3
x
= 5 + 2
y
Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т.е. задействовать
второетождественное преобразование.
Вот и делим:
Вот и всё. Мы
выразили икс через игрек. Слева – чистый икс, а справа – что уж получилось в результате «очищения» икса.
Можно было бы
сначалаподелить обе части на тройку, а затем – переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.
Напоминаю, что порядок преобразований никакой роли не играет. Как
намудобно, так и делаем. Самое главное – не порядок применения тождественных преобразований, а их
правильность!
А можно из этого же равенства
3
x
– 2
y
= 5
выразить y через
x
?
А почему – нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.
Первым делом избавляемся от выражения
3х. Перебрасываем его в правую часть:
–2
y
= 5 – 3
x
Осталась двойка с минусом. Делим обе части на (-2):
И все дела.) Мы
выразили
y
через х.Переходим к более серьёзным заданиям.
Как выразить переменную из формулы?
Не проблема!
Точно так же!Если понимать, что любая формула –
тоже уравнение.
Например, такое задание:
Из формулы
выразить переменную с.
Формула – тоже уравнение! Задание означает, что через преобразования из предложенной формулы нам надо получить какую-то
новую формулу.В которой слева будет стоять чистая
с, а справа – что уж получится, то и получится…
Однако… Как нам эту самую
свытаскивать-то?
Как-как… По шагам! Ясное дело, что выделить чистую
с
сразуневозможно: она в дроби сидит. А дробь умножается на
r… Значит, первым делом очищаем
выражение с буквой
с, т.е. всю дробь целиком.Здесь можно поделить обе части формулы на
r.
Получим:
Следующим шагом надо вытащить
сиз числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби – нету и числителя.) Умножаем обе части формулы на 2:
Осталась элементарщина. Обеспечим справа букве
сгордое одиночество. Для этого переменные
aи
bпереносим влево:
Вот и всё, можно сказать. Осталось переписать равенство в привычном виде, слева направо и – ответ готов:
Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле
где с = 1500 м/с – скорость звука в воде,
f
0
– частота испускаемых импульсов (в МГц),
f
– частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).
Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.
«Многа букафф», да… Но буквы – это лирика, а общая суть всё равно
та же самая. Первым делом надо выразить эту самую частоту отражённого сигнала (т.е. букву
f) из предложенной нам формулы. Вот этим и займёмся. Смотрим на формулу:
Напрямую, естественно, букву
fникак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там – видно будет. Для этого применяем
второепреобразование – умножаем обе части на знаменатель.
Получим:
А вот тут – очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)
Скобки слева означают, что буква
vумножается
на весь знаменатель целиком. А не на его отдельные кусочки…
Справа же, после умножения, дробь
исчезлаи остался одинокий числитель. Который, опять же,
весь
целикомумножается на буковку
с. Что и выражается скобками в правой части.)
А вот теперь скобки и раскрыть можно:
Отлично. Процесс идёт.) Теперь буковка
fслева стала
общим множителем. Выносим её за скобки:
Осталось всего ничего. Делим обе части на скобку
(
v
—
c
)и – дело в шляпе!
В принципе, всё готово. Переменная
f
уже выражена. Но можно дополнительно «причесать» полученное выражение – вынести
f
0за скобку в числителе и сократить всю дробь на (-1), тем самым избавившись от лишних минусов:
Вот такое выражение. А вот теперь и числовые данные подставить можно. Получим:
Ответ: 751 МГц
Вот и всё. Надеюсь, общая идея понятна.
Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь — не последовательность действий (она может быть любой), а их правильность.
В этих двух уроках рассматриваются лишь два базовых тождественных преобразования уравнений. Они работают
всегда. На то они и базовые. Помимо этой парочки, существует ещё множество других преобразований, которые тоже будут тождественными, но не всегда, а лишь
при определённых условиях.
Например, возведение обеих частей уравнения (или формулы) в квадрат (или наоборот, извлечение корня из обеих частей) будет тождественным преобразованием, если обе части уравнения
заведомо неотрицательны.
Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части
заведомо положительны.И так далее…
Подобные преобразования будут рассматриваться в соответствующих темах.
А здесь и сейчас — примеры для тренировки по элементарным базовым преобразованиям.
Простенькая задачка:
Из формулы
выразить переменную а и найти её значение при
S
=300,
V
0
=20,
t
=10.
Задачка посложнее:
Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:
где
V
1
и
V
2
– средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была
средняя скорость
лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?
Задача на основе реального варианта ОГЭ:
Центростремительное ускорение при движении по окружности (в м/с 2) можно вычислить по формуле
a
=ω 2
R
, где ω – угловая скорость (в с -1), а
R
– радиус окружности. Пользуясь этой формулой, найдите радиус
R
(в метрах), если угловая скорость равна 8,5 с -1 , а
центростремительное ускорение
равно 289 м/с 2.
Задача на основе реального варианта профильного ЕГЭ:
К источнику с ЭДС ε=155 В и внутренним сопротивлением
r
=0,5 Ом хотят подключить нагрузку с сопротивлением
R
Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.
Ответы (в беспорядке): 4; 15; 2; 10.
А уж где числа, километры в час, метры, омы – это как-нибудь сами…)
Способов
выведения неизвестной из формулы много, но как показывает опыт работы – все они
малоэффективны. Причина: 1. До 90% учащихся выпускных классов не умеют
правильно выразить неизвестное. Те же, кто умеют это делать – выполняют
громоздкие преобразования. 2. Физики, математики, химики – люди, которые
говорят на
разных языках
, объясняя методы переноса параметров через знак
равенства (предлагают правила треугольника, креста и др.) В статье рассмотрен простой алгоритм,
позволяющий в
один
прием, без многократного переписывания
выражения сделать вывод искомой формулы. Его можно мысленно сравнить с раздеванием человека (справа от равенства) в шкаф (слева): нельзя снять
рубашку, не снимая пальто или: то, что первым одевают, последним снимают.
Алгоритм:
1.
Записать формулу и разобрать прямой порядок выполняемых действий,
последовательность вычислений: 1) возведение в степень, 2) умножение –
деление, 3) вычитание – сложение.
2.
Записать:
(неизвестное) = (переписать
обратную часть равенства)(одежда в шкафу (слева от равенства) осталась на месте).
3. Правило преобразования формул: последовательность переноса параметров через
знак равенства определяется
обратной последовательностью вычислений. Найти в
выражении
последнее действиеи
перенестиего через знак равенства
первым. Поэтапно, находя последнее
действие в выражении, перенести сюда из другой части равенства (одежду с человека)
все известные величины. В обратной части равенства выполняются обратные
действия (если брюки снимают — «минус», то в шкаф укладывают — «плюс»).
Пример:
hv
=
hc
/
λ m
+
mυ
2
/2
Выразить
частоту
v
:
Порядок
действий: 1.
v
=
переписываем правую часть
hc
/
λ m
+
mυ
2
/2
2.
Разделим на
h
Итог:
v
= (
hc
/
λ m
+
mυ
2
/2) /
h
Выразить
υ
m
:
Порядок
действий: 1.
υ
m
= переписать левую часть (
hv
);
2. Последовательно переносим сюда с обратным знаком: (
—
hc
/λ
m
);
(*2); (
1/
m
);
(
√
или степень
1/2
).
Почему
сначала переносится (
—
hc
/λ
m
) ? Это последнее действие в правой части
выражения. Поскольку вся
правая часть
умножается на (
m
/2
),
то и вся левая часть делится на данный множитель: поэтому ставятся скобки.
Первое действие в правой части – возведение в квадрат, переносится в левую
часть последним.
Эту
элементарную математику с порядком действий при вычислениях каждый ученик
отлично знает. Поэтому
всеучащиеся довольно легко,
без многократного переписывания выражения,
сразу выводят формулу для вычисления неизвестного.
Итог:
υ
= ((
hv
—
hc
/λ
m
) *2/
m
) 0.5
`
(или
пишут квадратный корень вместо степени
0,5)
Выразить
λ
m
:
Порядок
действий: 1.
λ
m
= переписать левую часть (
hv
);
2.Вычесть (
mυ
2
/2
);
3. Разделить на (
hc
);
4. Возвести в степень (
-1
) (Математики обычно меняют
числитель и знаменатель искомого выражения.)
Чтобы вывести формулу сложного , нужно прежде всего путем анализа установить, из каких элементов состоит вещество и в каких весовых отношениях соединены друг с другом входящие в него элементы. Обычно состав сложного выражают в процентах, но он может быть выражен и в любых других числах, указывающих отноше
ние между весовыми количествами элементов, образующих данное вещество. Например, состав окиси алюминия, содержащей 52,94% алюминия и 47,06% кислорода, будет вполне определен, если мы скажем, что и соединены в весовом отношении 9:8, т. е. что на 9 вес. ч. алюминия приходится 8 вес. ч. кислорода. Понятно, что отношение 9: 8 должно равняться отношению 52,94: 47,06.
Зная весовой состав сложного и атомные веса образующих его элементов, нетрудно найти относительное число атомов каждого элемента в молекуле взятого вещества и таким образом установить его простейшую формулу.
Положим, например, что требуется вывести формулу хлористого кальция, содержащего 36% кальция и 64% хлора. Атомный вес кальция 40, хлора 35,5.
Обозначим число атомов кальция в молекуле хлористого кальция через
х,а число атомов хлора через
у.
Так как атом кальция весит 40, а атом хлора 35,5 кислородных единиц, общий вес атомов кальция, входящих в состав молекулы хлористого кальция, будет равен 40
х,а вес атомов хлора 35,5
у.
Отношение этих чисел, очевидно, должно равняться отношению весовых количеств кальция и хлора в любом количестве хлористого кальция. Но последнее отношение равно 36: 64.
Приравняв оба отношения, получим:
40x: 35,5y = 36:64
Затем освободимся от коэффициентов при неизвестных
хи
упутем деления первых членов пропорции на 40, а вторых на 35,5:
Числа 0,9 и 1,8 выражают относительное число атомов в молекуле хлористого кальция, но они дробны, тогда как в молекуле может содержаться только целое число атомов. Чтобы выразить отношение
х:
удвумя целыми числами, делим оба члена ^второго отношения на наименьший из них. Получаем
х:
у
= 1:2
Следовательно, в молекуле хлористого кальция на один атом кальция приходятся два атома хлора. Этому условию удовлетворяет целый ряд формул: СаСl 2 , Са 2 Сl 4 , Са 3 Сl 6 и т. д. Так как у нас нет данных, чтобы судить, какая из написанных формул отвечает действительному атомному составу молекулы хлористого кальция, мы остановимся на простейшей из них СаСl 2 , указывающей наименьшее возможное число атомов в молекуле хлористого кальция.
Однако произвол в выборе формулы отпадает, если наряду с весовым составом вещества известен также его молекулярный
вес. В этом случае нетрудно вывести формулу, выражающую истинный состав молекулы. Приведем пример.
Путем анализа установлено, что глюкоза содержит на 4,5 вес. ч. углерода 0,75 вес. ч. водорода и 6 вес. ч. кислорода. Молекулярный вес ее был найден равным 180. Требуется вывести формулу глюкозы.
Как и в предыдущем случае, находим сперва отношение между числом атомов углерода (атомный вес 12), водорода и кислорода в молекуле глюкозы. Обозначив число атомов углерода через
х,
водорода через
уи кислорода через
z,составляем пропорцию:
2х
:у:
16z = 4,5: 0,75: 6
откуда
Разделив все три члена второй половины равенства на 0,375, получаем:
х
:у:
z=
1: 2: 1
Следовательно, простейшая формула глюкозы будет СН 2 O. Но вычисленный по ней равнялся бы 30, тогда как в действительности глюкозы 180, т. е. в шесть раз больше. Очевидно, что для глюкозы нужно принять формулу C 6 H 12 O 6 .
Формулы, основанные, кроме данных анализа, также и на определении молекулярного веса и указывающие действительное число атомов в молекуле, называются истинными или молекулярнымиформулами; формулы же, выведенные только из данных анализа, называются простейшими или эмпирическими.
Познакомившись с выводом химических формул,» легко понять, как устанавливаются точные молекулярные веса. Как мы уже упоминали,
существующие методы
определения молекулярных весов в большинстве случаев не дают вполне точных результатов. Но, зная хотя бы приблизительный и процентный состав вещества, можно установить его формулу, выражающую атомный состав молекулы. Так как вес молекулы равняется сумме весов образующих ее атомов, сложив веса атомов, входящих в состав молекулы, мы определим ее вес в кислородных единицах, т. е. молекулярный вес вещества. Точность найденного молекулярного веса будет такой же, как и точность атомных весов.
Нахождение формулы химического соединения во многих случаях может быть значительно упрощено, если воспользоваться понятием овалентности элементов.
Напомним, что валентностью элемента называется свойство его атомов присоединять к себе или замещать определенное число атомов другого элемента.
Что такое валентность
элемента определяется числом, показывающим, сколько атомов водорода
(или
другого одновалентного элемента) присоединяет или замещает атом данного элемента.
Понятие о валентности распространяется не только на отдельные атомы, но и на целые группы атомов, входящие в состав
химических соединений
и участвующие как одно целое в химических реакциях. Такие группы атомов получили название радикалов. В неорганической химии наиболее важными радикалами являются: 1) водный остаток, или гидроксил ОН; 2) кислотные остатки; 3) основные остатки.
Водный остаток, или гидроксил, получается, если отмолекулы воды отнять один атом водорода. В молекуле воды гидроксил связан с одним атомом водорода, следовательно, группа ОН одновалентна.
Кислотными остатками называются группы атомов (аиногда и один атом), «остающиеся» от молекул кислот, если мысленно отнять от них один или несколько атомов водорода, замещаемых металлом. этих групп определяется числом отнятых атомов водорода. Например, дает два кислотных остатка — один двухвалентный SO 4
и другой одновалентный HSO 4 ,
входящий в состав различных кислых солей. Фосфорная кислотаН 3 РО 4
может дать три кислотных остатка: трехвалентный РО 4 ,
двухвалентный НРО 4
и одновалентный
Н 2 РО 4
и т. д.
Основными остатками мы будем называть; атомы или группы атомов, «остающиеся» от молекул оснований, если мысленно отнять от них один или несколько гидроксилов. Например, последовательно отнимая от молекулы Fe(OH) 3 гидроксилы, получаем следующие основные остатки: Fe(OH) 2 ,
FeOH и Fe. их определяется числом отнятых гидроксильных групп:Fe(OH) 2
— одновалентен; Fe(OH)-двухвалентен; Fe — трехвалентен.
Основные остатки, содержащие гидроксильные группы, входят в состав так называемых основных солей. Последние можно рассматривать как основания, в которых часть гидроксилов замещенакислотными остатками. Так, при замещении двух гидроксилов вFe(OH)3
кислотным остатком SO 4 получается основная соль FeOHSO 4 , при замещении одного гидроксила в Bi(OH) 3
кислотным остатком NO 3 получается основная соль Bi(OH) 2 NO 3 и т.д.
Знание валентностей отдельных элементов и радикалов позволяет в простых случаях быстро составлять формулы очень многих химических соединений, что освобождает химика от необходимости механически их заучивать.
Мнение эксперта:
Вывод формул физики и выражение переменных через другие являются важными аспектами в изучении науки. Опытные эксперты подчеркивают, что для успешного вывода формул и выражения переменных необходимо глубокое понимание математических принципов. Это требует уверенных знаний алгебры, геометрии и тригонометрии, а также умения применять их в контексте физических законов. Важно уметь адаптировать математические методы к конкретным физическим задачам, что подчеркивает важность союза между физикой и математикой. Эксперты считают, что умение выражать переменные из формул и выводить новые уравнения позволяет углубить понимание физических процессов и является ключевым навыком для успешной работы в области науки и техники.

Опыт других людей
Как выводить формулы физики и выражать переменные через другие – вопрос, который волнует многих. Люди отмечают, что такие навыки сильно помогают в изучении математики и физики. Они говорят, что союз с математикой делает понимание физических процессов более глубоким. Многие выражают благодарность за возможность лучше понять мир вокруг себя.
Интересные факты
- Использование размерности для проверки формул.Размерность физической величины — это показатель степени, в которую возведена единица измерения этой величины в формуле, выражающей зависимость между физическими величинами. Размерность можно использовать для проверки правильности формул. Если размерность левой и правой частей формулы не совпадает, то формула неверна.
- Метод подстановки.Метод подстановки — это метод решения уравнений, при котором одна переменная выражается через другую, а затем эта переменная подставляется в уравнение, содержащее другую переменную. Метод подстановки часто используется для решения уравнений, содержащих квадратные корни, степени и логарифмы.
- Метод логарифмирования.Метод логарифмирования — это метод решения уравнений, при котором обе части уравнения логарифмируются, а затем решается полученное уравнение. Метод логарифмирования часто используется для решения уравнений, содержащих экспоненты и степени.

Химические формулы
Пример 1.
Составить формулу гидрокарбоната кальция — кислой соли угольной кислоты.
В состав этой соли должны входить атомы кальция и одновалентные кислотные остатки НСО 3 . Так как двухвалентен, то на один атом кальция надо взять два кислотных остатка. Следовательно, формула соли будет Са(НСО 3)г.
В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ, в некоторых случаях необходимо только выразить неизвестную величину. Способов выведения неизвестной из формулы много. Если посмотреть страницы Интернета, то мы увидим множество рекомендаций по этому поводу. Это говорит о том, что единого подхода к решению этой проблемы научное сообщество еще не выработало, а те способы, которые используются, как показывает опыт работы в школе – все они малоэффективны. До 90% учащихся выпускных классов не умеют правильно выразить неизвестное. Те же, кто умеют это делать – выполняют громоздкие преобразования. Очень странно, но физики, математики, химики имеют разные подходы, объясняя методы переноса параметров через знак равенства (предлагают правила треугольника, креста или пропорций др.) Можно сказать, что имеют разную культуру работы с формулами. Можно представить, что происходит с большинством учеников, которые встречается с
разными трактовками
решения данной проблемы, последовательно посещая уроки этих предметов. Эту ситуацию описывает типичный диалог в сети:
Научите выражать из формул величины. 10 класс, мне стыдно не знать, как из одной формулы делать другую.
Да не переживай — это проблема многих моих одноклассников, хоть я и в 9 кл. Учителя показывают это чаще всего методом треугольника, но мне кажется, что это неудобно, да и запутаться легко. Покажу наиболее простой способ, которым я пользуюсь…
Допустим, дана формула:
Ну более простая….тебе из этой формулы нужно найти время. Ты берешь и в эту формулу подставляешь числа только разные, исходя из алгебры. Допустим:
и тебе наверное хорошо видно, что чтобы найти время в алгебраическом выражении 5 нужно 45/9 т.е переходим к физике: t=s/v
У большинства учащихся формируется психологический блок. Часто учащиеся отмечают, что при чтении учебника трудности в первую очередь вызывают те фрагменты текста, в которых много формул, что «длинные выводы все равно не понять», но при этом возникает чувство неполноценности, неверия в свои силы.
Я, предлагаю следующее решение данной проблемы – большинство учащихся все — таки могут решать примеры и, следовательно, расставлять порядок действий. Используем это их умение.
1
. В той части формулы, где содержится переменная, которую нужно выразить, надо расставь порядок действий, причем в одночленах, не содержащих искомую величину этого делать не будем.
2. Затем в обратной последовательности вычислений перенесите элементы формулы в другую часть формулы (через знак равенства) с противоположным действием (« минус» — «плюс», «разделить» — « умножить», « возведение в квадрат» – «извлечение корня квадратного»).
То есть найдем в выражении последнее действие и перенесем одночлен или многочлен, исполняющий это действие, через знак равенства первым, но уже с противоположным действием. Таким образом, последовательно, находя последнее действие в выражении, перенесите из одной части равенства в другую все известные величины. В заключение перепишем формулу так, чтобы неизвестная переменная стояла слева.
Получаем четкий алгоритм работы, точно знаем, сколько преобразований необходимо выполнить. Можем для тренировки использовать уже известные формулы, можем выдумывать свои. Для начала работы над усвоением данного алгоритма была создана презентация.
Опыт работы с учащимися показывает, что данный способ хорошо воспринимается ими. Реакция учителей на мое выступление на фестивале «Учитель профильной школы» также говорит о положительном зерне, заложенном в этой работе.
Возможно, будет полезно почитать:
- Дело об убийстве царской семьи: что говорят в РПЦ Телеграммы великой драмы
; - Чуть в стороне от царского пути
; - Икона Божьей Матери «Неупиваемая чаша
; - Псориаз: лечение с помощью заговора Церковные православные молитвы от псориаза
; - Преподобный Мефодий Пешношский – основатель Николо-Пешношского монастыря
; - ПП чизкейк: вкусные диетические рецепты Диетический шоколадный чизкейк
; - Вредны ли чипсы Pringles?
; - Подсчитываем калории: в вашей тарелке – печенка говядины
;
Частые вопросы
Как в уравнении выразить одну переменную через другую?
Для того, чтобы выразить одну переменную через другую, нужно с левой стороны равенства оставить значения с одной переменой, а с правой стороны оставить значения с другой переменной и свободные члены. Далее необходимо избавиться от коэффициента при переменной с левой стороны. c + 5 * d = 30. c = 30 – 5 * d.
Как правильно выразить переменную из формулы?
Что значит вывести формулу?
Выводом из конечной совокупности формул H называется всякая конечноая последовательность формул , всякий член которой удовлетворяет одному из следующих трех условий: 1) является одной из формул совокупности H, 2) является доказуемой формулой, 3) получается по правилу заключения из двух любых предшествующих членов …
Как найти силу F в физике?
F=ma. Формула F=ma выражает второй закон Ньютона, который формулируют так: сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этому телу силой.

Полезные советы
СОВЕТ №1
Изучите основные законы физики и математики, такие как законы Ньютона, законы сохранения энергии и импульса, а также основные математические операции, чтобы понимать, как выражать одну переменную через другую.
СОВЕТ №2
Используйте алгебраические методы для выражения переменных из формул. Например, для выражения переменной из уравнения, используйте алгебраические преобразования, чтобы изолировать нужную переменную.
СОВЕТ №3
Практикуйтесь в решении задач и применении формул на практике, чтобы лучше понимать, как выражать переменные и применять их в различных физических задачах.