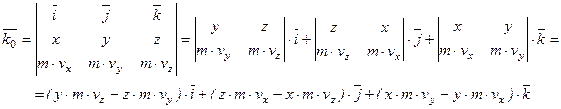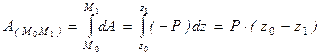В некоторых задачах в качестве динамической характеристики движущейся точки вместо самого количества движения рассматривают его момент относительно какого-либо центра или оси. Эти моменты определяются также как и моменты силы.
Моментом количеством движения
материальной точки относительно некоторого центра О называется вектор, определяемый равенством
Момент количества движения точки называют также
кинетическим моментом
.
Момент количества движения
относительно какой-либо оси , проходящий через центр О, равен проекции вектора количества движения на эту ось .
Если количество движения задано своими проекциями на оси координат и даны координаты точки в пространстве, то момент количества движения относительно начала координат вычисляется следующим образом:
Проекции момента количества движения на оси координат равны:
Единицей измерения количества движения в СИ является – .
Конец работы —
Эта тема принадлежит разделу:
Динамика
Лекция.. краткое содержание введение в динамику аксиомы классической механики.. введение..
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Все темы данного раздела:
Системы единиц
СГС
Си
Техническая
[L]
см
м
м
[M]
Дифференциальные уравнения движения точки
Основное уравнение динамики
можно записать так
Основные задачи динамики
Первая или прямая задача:
Известна масса точки и закон ее движения, необходимо найти действующую на точку силу.
m
Наиболее важные случаи
1. Сила постоянна.
Количество движения точки
Количеством движения материальной точки называется вектор, равный произведению м
Элементарный и полный импульс силы
Действие силы на материальную точку в течении времени
Теорема об изменении количества движения точки
Теорема. Производная по времени от количества движения точки равна действующей на точку силе.
Запишем основной закон динамики
Теорема об изменении момента количества движения точки
Теорема. Производная по времени от момента количества движения точки, взятого относительно какого-нибудь центра, равна моменту действующей на точку силы относительно того же
Работа силы. Мощность
Одна из основных характеристик силы, оценивающих действие силы на тело при некотором его перемещении.
Теорема об изменении кинетической энергии точки
Теорема. Дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.
Принцип Даламбера для материальной точки
Уравнение движения материальной точки относительно инерциальной системы отсчета под действием приложенных активных сил и сил реакции связей имеет вид:
Динамика несвободной материальной точки
Несвободной материальной точкой называется точка, свобода движения которой ограничена.
Тела, ограничивающие свободу движения точки, называются связями
Относительное движение материальной точки
Во многих задачах динамики движение материальной точки рассматривается относительно системы отсчета, движущейся относительно инерциальной системы отсчета.
Частные случаи относительного движения
1. Относительное движение по инерции
Если материальная точка движется относительно подвижной системы отсчета прямолинейно и равномерно, то такое движение называется относительны
Геометрия масс
Рассмотрим механическую систему, которая состоит из конечного числа материальных точек с массами
Моменты инерции
Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.
Момент инерции относительно точки
Моменты инерции простейших тел
1. Однородный стержень
2. Прямоугольная пластина
3. Однородный круглый диск
Количество движения системы
Количеством движения системы материальных точек называется векторная сумма колич
Теорема об изменении количества движения системы
Эта теорема существует в трех различных формах.
Теорема. Производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих н
Законы сохранения количества движения
1. Если главный вектор всех внешних сил системы равен нулю (), то количество движения системы постоянно
Теорема о движении центра масс
Теорема Центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к рассмат
Момент количества движения системы
Моментом количества движения системы материальных точек относительно некоторого
Момент количества движения твердого тела относительно оси вращения при вращательном движении твердого тела
Вычислим момент количества движения твердого тела относительно оси вращения.
Теорема об изменении момента количества движения системы
Теорема. Производная по времени от момента количества движения системы, взятого относительно какого-нибудь центра, равна векторной сумме моментов внешних сил, действующих на
Законы сохранения момента количества движения
1. Если главный момент внешних сил системы относительно точки равен нулю (
Кинетическая энергия системы
Кинетической энергией системы называют сумму кинетических энергий всех точек системы.
Кинетическая энергия твердого тела
1. Поступательное движение тела.
Кинетическая энергия твердого тела при поступательном движении вычисляется так же, как и для одной точки, у которой масса равна массе этого тела.
Теорема об изменении кинетической энергии системы
Эта теорема существует в двух формах.
Теорема. Дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систе
В некоторых задачах в качестве динамической характеристики движущейся точки вместо самого количества движения рассматривают его момент относительно какого-либо центра или оси. Эти моменты определяются также как и моменты силы.
Моментом количеством движения
материальной точки относительно некоторого центра О называется вектор, определяемый равенством
Момент количества движения точки называют также
кинетическим моментом
.
Момент количества движения
относительно какой-либо оси , проходящий через центр О, равен проекции вектора количества движения на эту ось .
Если количество движения задано своими проекциями на оси координат и даны координаты точки в пространстве, то момент количества движения относительно начала координат вычисляется следующим образом:
Проекции момента количества движения на оси координат равны:
Единицей измерения количества движения в СИ является – .
Теорема об изменении момента количества движения точки.
Теорема.
Производная по времени от момента количества движения точки, взятого относительно какого-нибудь центра, равна моменту действующей на точку силы относительно того же центра.
Доказательство: Продифференцируем момент количества движения по времени
,
, следовательно , (*)
что и требовалось доказать.
Теорема.
Производная по времени от момента количества движения точки, взятого относительно какой-либо оси, равна моменту действующей на точку силы относительно той же оси.
Для доказательства достаточно спроектировать векторное уравнение (*) на эту ось. Для оси это будет выглядеть так:
Следствия из теорем:
1. Если момент силы относительно точки равен нулю, то момент количества движения относительно этой точки величина постоянная.
2. Если момент силы относительно оси равен нулю, то момент количества движения относительно этой оси величина постоянная.
Работа силы. Мощность.
Одна из основных характеристик силы, оценивающих действие силы на тело при некотором его перемещении.
Элементарная работа силы
скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.
Единицей измерения работы в СИ является –
При при
Частные случаи:
Элементарное перемещение равно дифференциалу радиуса вектора точки приложения силы.
Элементарная работа силы
равна скалярному произведению силы на элементарное перемещение или на дифференциал радиуса вектора точки приложения силы.
Элементарная работа силы
равна скалярному произведению элементарного импульса силы на скорость точки.
Если сила задана своими проекциями () на оси координат и элементарное перемещение задано своими проекциями () на оси координат, то элементарная работа силы равна:
(аналитическое выражение элементарной работы).
Работа силы на любом конечном перемещении равна взятому вдоль этого перемещения интегралу от элементарной работы.
Мощностью силы
называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы.
,
Мощность
равна скалярному произведению силы на скорость.
Единицей измерения мощности в СИ является –
В технике за единицу силы принимается
.
Пример 1. Работа силы тяжести.
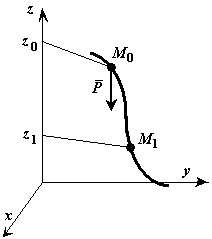
Пусть точка М, на которую действует сила тяжести Р, перемещается из положения
в положение . Выберем оси координат так, чтобы ось была направлена вертикально вверх.
Тогда, , , и
Работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной.
Пример 2. Работа силы упругости.
Рассмотрим материальную точку закрепленную на упругом элементе жесткости с, которая совершает колебания вдоль оси х. Сила упругости (или восстанавливающая сила) . Пусть точка М, на которую действует только сила упругости, перемещается из положения в положение . ( , ).
Мощность пары сил равна
Кинетическая энергия точки
Кинетической энергией материальной точки
(или ее живой силой) называют половину произведения массы точки на квадрат ее скорости.
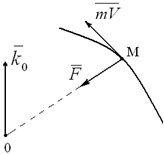
Рассмотрим материальную точку
Mмассой
m, движущуюся под действием силы
F(рисунок 3.1). Запишем и построим вектор момента количества движения (кинетического момента)
M 0материальной точки относительно центра
O:
Рисунок 3.1
Дифференцируем выражение момента количества движения (кинетического момента
k 0) по времени:
Так как
dr/dt=V, то векторное произведение
V × m∙V(коллинеарных векторов
Vи
m∙V) равно нулю. В то же время
d(m∙V)/dt=Fсогласно теореме о количестве движения материальной точки . Поэтому получаем, что
dk 0 /dt = r×F, (3.3)
где
r×F = M 0 (F)– вектор-момент силы
Fотносительно неподвижного центра
O. Вектор
k 0⊥ плоскости (
r, m×V), а вектор
M 0 (F)⊥ плоскости (
r, F), окончательно имеем
dk 0 /dt = M 0 (F). (3.4)
Уравнение (3.4) выражает теорему об изменении момента количества движения (кинетического момента) материальной точки относительно центра:
производная по времени от момента количества движения (кинетического момента) материальной точки относительно какого-либо неподвижного центра равна моменту действующей на точку силы относительно того же центра.
Проецируя равенство (3.4) на оси декартовых координат, получаем
dk x /dt = M x (F);
dk y /dt = M y (F);
dk z /dt = M z (F). (3.5)
Равенства (3.5) выражают теорему об изменении момента количества движения (кинетического момента) материальной точки относительно оси:
производная по времени от момента количества движения (кинетического момента) материальной точки относительно какой-либо неподвижной оси равна моменту действующей на эту точку силы относительно той же оси.
Рассмотрим следствия, вытекающие из теорем (3.4) и (3.5).
Мнение эксперта:
Момент количества движения системы играет важную роль в физике и механике. Эксперты отмечают, что изменение момента количества движения может происходить под воздействием внешних сил или внутренних процессов в системе. Это может привести к изменению скорости, направления движения или распределения масс в системе. Понимание этого является ключевым для анализа динамики объектов и развития технологий, основанных на принципах сохранения и изменения момента количества движения.

Следствие 1
Рассмотрим случай, когда сила
Fво все время движения точки проходит через неподвижный центр
O(случай центральной силы), т.е. когда
M 0 (F) = 0. Тогда из теоремы (3.4) следует, что
k 0 = const,
т.е. в случае центральной силы момент количества движения (кинетический момент) материальной точки относительно центра этой силы остается постоянным по модулю и направлению(рисунок 3.2).
Рисунок 3.2
Из условия
k 0 = constследует, что траектория движущейся точки представляет собой плоскую кривую, плоскость которой проходит через центр этой силы.
Интересные факты
-
Момент количества движения системы сохраняется, если на нее не действуют внешние силы.Это означает, что если система замкнута, то ее суммарный момент количества движения остается постоянным. Этот закон является одним из фундаментальных законов физики и имеет множество применений в различных областях науки и техники.
-
Изменение момента количества движения системы равно импульсу внешних сил, действующих на систему.Это означает, что если на систему действуют внешние силы, то ее суммарный момент количества движения будет изменяться. Величина изменения момента количества движения равна импульсу внешних сил, действующих на систему.
-
Момент количества движения системы может быть изменен путем изменения распределения масс в системе.Например, если в системе есть вращающийся объект, то его момент количества движения можно изменить, изменив распределение масс в объекте. Это можно сделать, например, путем перемещения масс ближе к центру вращения или дальше от него.

Опыт других людей
Момент количества движения системы — это важный физический параметр, о котором говорят многие специалисты и ученые. Изменение момента количества движения может привести к различным последствиям, которые обсуждаются в научных кругах. Люди высказывают разные мнения о том, как изменение этого параметра влияет на движение системы и ее поведение в пространстве. Некоторые утверждают, что изменение момента количества движения может привести к изменению траектории движения, в то время как другие считают, что это влияет на общую кинетическую энергию системы. Обсуждение этой темы продолжается в научных кругах, и каждый высказывает свое мнение на этот счет.
Следствие 2
Пусть
M z (F) = 0, т.е. сила пересекает ось
zили параллельна ей.
В этом случае, как это видно из третьего из уравнений (3.5),
k z = const,
т.е. если момент действующей на точку силы относительно какой-либо неподвижной оси всегда равен нулю, то момент количества движения (кинетический момент) точки относительно этой оси остается постоянным.
- 1.
Алгебраическиймомент количества движения относительно центра.
Алгебраический
О— скалярная величина, взятая со знаком (+) или (-) и равная произведению модуля количества движения
mна расстояние
h(перпендикуляр) от этого центра до линии, вдоль которой направлен вектор
m: - 2. Векторный момент количества движения относительно центра.
Векторныймомент количества движения материальной точки относительно некоторого центра
О —вектор, приложенный в этом центре и направленный перпендикулярно плоскости векторов
mи
в ту сторону, откуда движение точки видно против хода часовой стрелки. Это определение удовлетворяет векторному равенству
Моментом количества движенияматериальной точки относительно некоторой оси
zназывается скалярная величина, взятая со знаком (+) или (-) и равная произведению модуля
проекции вектора
количества движения на плоскость, перпендикулярную этой оси, на перпендикуляр
h,опущенный из точки пересечения оси с плоскостью на линию, вдоль которой направлена указанная проекция:
Кинетический момент механической системы относительно центра и оси
1. Кинетический момент относительно центра.
Кинетическим моментомили главным моментом количеств движения механической системы относительно некоторого
центраназывается геометрическая сумма моментов количеств движения всех материальных точек системы относительно того же центра.
2. Кинетический момент относительно оси.
Кинетическим моментом или главным моментом количеств движения механической системы относительно некоторой оси называется алгебраическая сумма моментов количеств движения всех материальных точек системы относительно той же оси.
3. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси z с угловой скоростью.
Теорема об изменении момента количества движения материальной точки относительно центра и оси
1. Теорема моментов относительно центра.
Производнаяпо времени от момента количества движения материальной точки относительно некоторого неподвижного центра равна моменту силы, действующей на точку, относительно того же центра
2. Теорема моментов относительно оси.
Производнаяпо времени от момента количества движения материальной точки относительно некоторой оси равна моменту силы, действующей на точку, относительно той же оси
Теорема об изменении кинетического момента механической системы относительно центра и оси
Теорема моментов относительно центра.
Производнаяпо времени от кинетического момента механической системы относительно некоторого неподвижного центра равна геометрической сумме моментов всех внешних сил, действующих на систему, относительно того же центра;
Следствие.Если главный момент внешних сил относительно некоторого центра равен нулю, то кинетический момент системы относительно этого центра не изменяется (закон сохранения кинетического момента).
2. Теорема моментов относительно оси.
Производнаяпо времени от кинетического момента механической системы относительно некоторой неподвижной оси равна сумме моментов всех внешних сил, действующих на систему, относительно этой оси
Следствие.Если главный момент внешних сил относительно некоторой оси равен нулю, то кинетический момент системы относительно этой оси не изменяется.
Например, =0, тогда
L
z
= const.
Работа и мощность сил
Работа силы— скалярная мера действия силы.
1. Элементарная работа силы.
Элементарнаяработа силы — это бесконечно малая скалярная величина, равная скалярному произведению вектора силы на вектор бесконечного малого перемещения точки приложения силы:
;
—приращение радиуса-вектора
точки приложения силы, годографом которого является траектория этой точки. Элементарное перемещение
точки по траектории совпадает с
в силу их малости. Поэтому
если то
dA >0;если, то
dA =0;если
,то
dA 0.
2. Аналитическое выражение элементарной работы.
Представим векторы
и
dчерез их проекции на оси декартовых координат:
, .Получим (4.40)
3. Работа силы на конечном перемещении равна интегральной сумме элементарных работ на этом перемещении
Если сила постоянная, а точка ее приложения перемещается прямолинейно,
4. Работа силы тяжести. Используем формулу:Fx = Fy = 0; Fz = -G = -mg;
где
h-перемещение точки приложения силы по вертикали вниз (высота).
При перемещении точки приложения силы тяжести вверх
A12 =
-mgh(точка
М
1
—внизу,
M2 — вверху).
Итак,
.Работа силы тяжести не зависит от формы траектории. При движении по замкнутой траектории (
M2 совпадает с
М
1
)работа равна нулю.
5. Работа силы упругости пружины.
Пружина растягивается только вдоль оси
х:
F
y
=
F
z
=О,
F
x
==
-сх;
где — величина деформации пружины.
При перемещении точки приложения силы из нижнего положения в верхнее направление силы и направление перемещения совпадают, тогда
Поэтому работа силы упругости
Работа сил на конечном перемещении; Если = const, то
где — конечный угол поворота; , где
п —число оборотов тела вокруг оси.
Кинетическая энергия материальной точки и механической системы. Теорема Кенига
Кинетическая энергия— скалярная мера механического движения.
Кинетическая энергия материальной точки —скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости,
Кинетическая энергия механической системы —арифметическая сумма кинетических энергий всех материал точек этой системы:
Кинетическая энергия системы, состоящей из
псвязанных между собой тел, равна арифметической сумме кинетических энергий всех тел этой системы:
Теорема Кенига
Кинетическая энергия механической системыв общем случае ее движения равна сумме кинетической энергии движения системы вместе с центром масс и кинетической энергии системы при ее движении относительно центра масс:
где
Vkc —скорость
k-й
точки системы относительно центра масс.
Кинетическая энергия твердого тела при различном движении
Поступательное движение.
Вращение тела вокруг неподвижной оси
. ,где —
момент инерции тела относительно оси вращения.
3. Плоскопараллельное движение. , где — момент инерции плоской фигуры относительно оси, проходящей через центр масс.
При плоском движениитела кинетическая энергия складывается из кинетической энергии поступательного движения тела со скоростью центра масс
и кинетической энергии вращательного движения вокруг оси, проходящей через центр масс, ;
Теорема об изменении кинетической энергии материальной точки
Теорема в дифференциальной форме.
Дифференциалот кинетической энергии материальной точки равен элементарной работе силы, действующей на точку,
Теорема в интегральной (конечной) форме.
Изменениекинетической энергии материальной точки на некотором перемещении равно работе силы, действующей на точку, на том же перемещении.
Теорема об изменении кинетической энергии механической системы
Теорема в дифференциальной форме.
Дифференциалот кинетической энергии механической системы равен сумме элементарных работ внешних и внутренних сил, действующих на систему.
Теорема в интегральной {конечной) форме.
Изменениекинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, приложенных к системе, на том же перемещении. ; Для системы твердых тел = 0 (по свойству внутренних сил). Тогда
Закон сохранения механической энергии материальной точки и механической системы
Если на материальнуюточку или механическую систему действуют только консервативные силы, то в любом положении точки или системы сумма кинетической и потенциальной энергий остается величиной постоянной.
Для материальной точки
Для механической системы
Т+ П=const
где
Т+ П —полная механическая энергия системы.
Динамика твердого тела
Дифференциальные уравнения движения твердого тела
Эти уравнения можно получить из общих теорем динамики механической системы.
1. Уравнения поступательного движения тела — из теоремы о движении центра масс механической системы В проекциях на оси декартовых координат
2. Уравнение вращения твердого тела вокруг неподвижной оси — из теоремы об изменении кинетического момента механической системы относительно оси, например, относительно оси
Так как кинетический момент
L
z
твердого тела относительно оси, то если
Так как или, то уравнение можно записать в виде или,форма записи уравнения зависит от того, что следует определить в конкретной задаче.
Дифференциальные уравнения плоскопараллельногодвижения твердого тела представляют собой совокупность уравнений
поступательногодвижения плоской фигуры вместе с центром масс и
вращательногодвижения относительно оси, проходящей через центр масс:
Физический маятник
Физическим маятникомназывается твердое тело, вращающееся вокруг горизонтальной оси, не проходящей через центр масс тела, и движущееся под действием силы тяжести.
Дифференциальное уравнение вращения
В случае малых колебаний.
Тогда, где
Решение этого однородного уравнения.
Пусть при
t=0Тогда
—уравнение гармонических колебаний.
Период колебаний маятника
Приведенная длинафизического маятника — это длина такого математического маятника, период колебаний которого равен периоду колебаний физического маятника.
Момент количества движения
моме́нт коли́чества движе́ния
(кинетический момент, момент импульса, угловой момент), мера механического движения тела или системы тел относительно какого-либо центра (точки) или оси. Для вычисления момента количества движения
Kматериальной точки (тела) справедливы те же формулы, что и для вычисления момента силы, если заменить в них вектор силы на вектор количества движения
mv, т. е.
K= [
r·
mv], где
r— расстояние до оси вращения. Сумма моментов количества движения всех точек системы относительно центра (оси) называется главным моментом количества движения системы (кинетическим моментом) относительно этого центра (оси). При вращательном движении твёрдого тела главный момент количества движения относительно оси вращения
z
I zна угловую скорость ω тела, т. е.
K z=
I zω.
МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
МОМЕ́НТ КОЛИ́ЧЕСТВА ДВИЖЕ́НИЯ (кинетический момент, момент импульса, угловой момент), мера механического движения тела или системы тел относительно какого-либо центра (точки) или оси. Для вычисления момента количества движения
Кматериальной точки (тела) справедливы те же формулы, что и для вычисления момента силы
(
см.МОМЕНТ СИЛЫ)
, если заменить в них вектор силы на вектор количества движения
mv, в частности
K0 = [
r·
mv]. Сумма моментов количества движения всех точек системы относительно центра (оси) называется главным моментом количества движения системы (кинетическим моментом) относительно этого центра (оси). При вращательном движении твердого тела главный момент количества движения относительно оси вращения
zтела выражается произведением момента инерции
(
см.МОМЕНТ ИНЕРЦИИ)
Iz на угловую скорость w тела, т. е.
КZ =
Iz w.
Энциклопедический словарь
.
2009
.
Смотреть что такое «момент количества движения» в других словарях:
— (кинетический момент, угловой момент), одна из мер механич. движения материальной точки или системы. Особенно важную роль М. к. д. играет при изучении вращат. движения. Как и для момента силы, различают М. к. д. относительно центра (точки) и… …
Физическая энциклопедия
— (кинетический момент Момент импульса, угловой Момент), мера механического движения тела или системы тел относительно какого либо центра (точки) или оси. Для вычисления момента количества движения К материальной точки (тела) справедливы те же… …
Большой Энциклопедический словарь
Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси… … Википедия
момент количества движения— кинетический момент, одна из мер механического движения материальной точки или системы. Особенно важную роль момент количества движения играет при изучении вращательного движения. Как и для момента силы, различают момент… …
Энциклопедический словарь по металлургии
момент количества движения— judesio kiekio momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus dalelės padėties vektoriaus iš tam tikro taško į dalelę ir jos judesio kiekio vektorinei sandaugai, t. y. L = r · p; čia L – judesio kiekio momento… …
момент количества движения— judesio kiekio momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Materialiojo taško arba dalelės spindulio vektoriaus ir judesio kiekio vektorinė sandauga. Dažniausiai apibūdina sukamąjį judesį taško arba ašies, iš kurios yra… …
Penkiakalbis aiškinamasis metrologijos terminų žodynas
момент количества движения— judesio kiekio momentas statusas T sritis fizika atitikmenys: angl. angular moment; moment of momentum; rotation moment vok. Drehimpuls, m; Impulsmoment, n; Rotationsmoment, n rus. момент импульса, m; момент количества движения, m; угловой момент … Fizikos terminų žodynas
Кинетический момент, одна из мер механического движения материальной точки или системы. Особенно важную роль М. к. д. играет при изучении вращательного движения (См. Вращательное движение). Как и для момента силы (См. Момент силы),… …
Большая советская энциклопедия
— (кинетич. момент, момент импульса, угловой момент), мера механич. движения тела или системы тел относительно к. л. центра (точки) или осн. Для вычисления М. к. д. К материальной точки (тела) справедливы те же формулы, что и для вычисления момента …
Естествознание. Энциклопедический словарь
То же, что момент импульса …
Большой энциклопедический политехнический словарь
Книги
- Сочинения , Карл Маркс. Второй том Сочинений К. Маркса и Ф. Энгельса содержит произведения, написанные с сентября 1844 по февраль 1846 года. В конце августа 1844 г. в Париже произошла встреча Маркса и Энгельса,…
- Теоретическая механика. Динамика металлоконструкций , В. Н. Шинкин. Рассмотрены основные теоретические и практические вопросы динамики материальной системы и аналитической механики по следующим темам: геометрия масс, динамика материальной системы и твердого…
Возможно, будет полезно почитать:
- ПП чизкейк: вкусные диетические рецепты Диетический шоколадный чизкейк
; - Вредны ли чипсы Pringles?
; - Подсчитываем калории: в вашей тарелке – печенка говядины
; - Бульонные кубики магги Бульонные кубики Магги — польза и вред
; - Голубой сыр с плесенью — полезные свойства и рецепт
; - Безе: состав, калорийность, энергетическая ценность, польза и вред Безе калорийное
; - Что написать в резюме в разделе «обо мне
; - Срок давности по неоплаченным кредитам: какой он
;

Частые вопросы
Как формулируется закон изменения количества движения?
Формулировка теоремы Теорема об изменении количества движения системы утверждает: Изменение количества движения системы за некоторый промежуток времени равно импульсу внешних сил, действующих на систему, за тот же промежуток времени.
Что называется количеством движения системы?
Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость: . Её также называют импульсом материальной точки. Количеством движения материальной системы называется геометрическая сумма количеств движения всех точек системы: .
Как рассчитать момент количества движения?
Т. о., ko = [r · mu], где r — радиус-вектор движущейся точки, проведённый из центра О, a kz равняется проекции вектора ko на ось z, проходящую через точку О. Изменение М.
Как определить количество движения?
Импульсом (или количеством движения) материальной точки называют физическую величину, определяемую произведением её массы на вектор скорости в данной системе отсчёта:
vec p = m * vec v
Полезные советы
СОВЕТ №1
Понимание закона сохранения момента количества движения поможет вам лучше понять изменения, происходящие в системе. Уделите время изучению этого закона и его применению в различных ситуациях.
СОВЕТ №2
Изучите примеры изменения момента количества движения в различных физических системах. Практические примеры помогут вам лучше усвоить материал и научиться применять его на практике.