Родоначальниками «петлевой квантовой теории гравитации» в 80-е годы XX века являются Ли Смолин (Lee Smolin), Абэй Аштекар (Abhay Ashtekar), Тэд Джекобсон (Ted Jacobson) и Карло Ровелли (Carlo Rovelli). Согласно этой теории, пространство и время действительно состоят из дискретных частей. Эти маленькие квантовые ячейки пространства определённым способом соединены друг с другом, так что на малых масштабах времени и длины они создают пёструю, дискретную структуру пространства, а на больших масштабах плавно переходят в непрерывное гладкое пространство-время . Хотя многие космологические модели могут описать поведение Вселенной только от Планковского времени после Большого Взрыва , петлевая квантовая гравитация может описать сам процесс взрыва, и даже заглянуть раньше. Но встаёт проблема выбора координат. Можно сформулировать общую теорию относительности (ОТО) в бескоординатной форме, например, с помощью внешних форм, однако, вычисления 4-формы Римана мы будем осуществлять в конкретной метрике. Любош Мотль — один из самых активных и остроумных пропагандистов теории струн — по этому поводу выразился так, что говорить, например, о «фоновой независимости» пропагатора спиновой сети петлевой теории гравитации без указания единичного состояния — то же самое, что вычислять ряд Тейлора в точке х 0 без указания х 0 .
Петлевая гравитация и физика элементарных частиц
Одним из преимуществ петлевой квантовой теории гравитации является естественность, с которой в ней получает своё объяснение Стандартная модель физики элементарных частиц.
Таким образом, Бильсон-Томпсон с соавторами предположили, что теория петлевой квантовой гравитации может воспроизвести стандартную модель, автоматически объединяя все четыре фундаментальных взаимодействия. При этом с помощью преонов, представленных в виде брэдов (переплетений волокнистого пространства-времени) удалось построить успешную модель первого семейства фундаментальных фермионов (кварков и лептонов) с более-менее правильным воспроизведением их зарядов и четностей .
В исходной статье Бильсона-Томпсона предполагалось, что фундаментальные фермионы второго и третьего семейств могут быть представлены в виде более сложных брэдов, а фермионы первого семейства представляются простейшими из возможных брэдов, хотя конкретных представлений сложных брэдов не давалось. Считается, что электрический и цветовой заряды, а также чётность частиц, принадлежащих к семействам более высокого ранга, должны получаться точно таким же образом, как и для частиц первого семейства.
Использование методов квантовых вычислений позволило показать, что такого рода частицы устойчивы и не распадаются под действием квантовых флуктуаций .
Ленточные структуры в модели Бильсона-Томпсона представлены в виде сущностей, состоящих из той же материи, что и само пространство-время . Хотя в статьях Бильсона-Томпсона и показано, как из этих структур можно получить фермионы и бозоны , вопрос о том, как с помощью брэдинга можно было бы получить бозон Хиггса , в них не обсуждается.
Л. Фрейдель (L. Freidel), Дж. Ковальский-Гликман (J. Kowalski-Glikman) и А. Стародубцев (A. Starodubtsev) в своей статье 2006 года высказали предположение, что элементарные частицы можно представить с помощью линий Вильсона гравитационного поля, подразумевая, что свойства частиц (их массы, энергии и спины) могут соответствовать свойствам петель Вильсона — базовым объектам теории петлевой квантовой гравитации. Эту работу можно рассматривать в качестве дополнительной теоретической поддержки преонной модели Бильсона-Томпсона .
Используя формализм модели спиновой пены, имеющей непосредственное отношение к теории петлевой квантовой гравитации, и базируясь лишь на исходных принципах последней, можно также воспроизвести и некоторые другие частицы стандартной модели, такие как фотоны , глюоны и гравитоны — независимо от схемы брэдов Бильсона-Томпсона для фермионов. Однако, по состоянию на 2006 год, с помощью этого формализма пока не удалось построить модели гелонов. В модели гелонов отсутствуют брэды, которые можно было бы использовать для построения бозона Хиггса, но в принципе данная модель не отрицает возможности существования этого бозона в виде некоей композитной системы. Бильсон-Томпсон отмечает, что, поскольку частицы с бо́льшими массами в основном имеют более сложную внутреннюю структуру (учитывая также перекручивание брэдов), то эта структура возможно имеет отношение к механизму формирования массы. Например, в модели Бильсона-Томпсона структура фотона, имеющего нулевую массу, соответствует неперекрученным брэдам. Правда пока остается неясным, соответствует ли модель фотона, полученная в рамках формализма спиновой пены , фотону Бильсона-Томпсона, который в его модели состоит из трех незакрученных риббонов , (возможно, что в рамках формализма спиновой пены можно построить несколько вариантов модели фотона).
Первоначально понятие «преон» использовалось для обозначения точечных субчастиц, входящих в структуру фермионов с половинным спином (лептонов и кварков). Как уже упоминалось, использование точечных частиц приводит к парадоксу массы. В модели Бильсона-Томпсона риббоны не являются «классическими» точечными структурами. Бильсон-Томпсон использует термин «преон» для сохранения преемственности в терминологии, но обозначает с помощью этого термина более широкий класс объектов, являющихся компонентами структуры кварков, лептонов и калибровочных бозонов.
Важным для понимания подхода Бильсона-Томпсона является то, что в его преонной модели элементарные частицы, такие как электрон , описываются в терминах волновых функций. Сумма квантовых состояний спиновой пены, имеющих когерентные фазы, также описывается в терминах волновой функции. Поэтому возможно, что с помощью формализма спиновой пены можно получить волновые функции, соответствующие элементарным частицам (фотонам и электронам). В настоящее время объединение теории элементарных частиц с теорией петлевой квантовой гравитации является весьма активной областью исследований .
В октябре 2006 г. Бильсон-Томпсон модифицировал свою статью , отмечая, что, хотя его модель и была инспирированна преонными моделями, но она не является преонной в строгом смысле этого слова, поэтому топологические диаграммы из его преонной модели скорее всего можно использовать и в других фундаментальные теориях, таких как, например, М-теория . Теоретические ограничения, накладываемые на преонные модели, неприменимы к его модели, поскольку в ней свойства элементарных частиц возникают не из свойств субчастиц, а из связей этих субчастиц друг с другом (брэдов). В модифицированной версии его статьи Бильсон-Томпсон признает, что нерешенными проблемами в его модели остаются спектр масс частиц, спины , смешивание Каббибо, а также необходимость привязки его модели к более фундаментальным теориям. Одной из возможностей является, например, «встраивание» преонов в М-теорию или в теорию петлевой квантовой гравитации.
В более позднем варианте статьи описывается динамика брэдов с помощью переходов Пачнера (Pachner moves).
Мнение эксперта:
Эксперты в области физики и квантовой теории выражают различные мнения относительно петлевой квантовой теории гравитации. Некоторые ученые считают, что данная теория представляет собой перспективный подход к объединению общей теории относительности и квантовой механики. Они отмечают, что петлевая квантовая теория гравитации позволяет учитывать квантовые эффекты в гравитационном поле, что является важным шагом в понимании фундаментальных взаимодействий в природе. Однако другие ученые высказывают сомнения относительно эффективности данной теории и указывают на необходимость дальнейших экспериментов и исследований для подтверждения ее предсказаний. Таким образом, петлевая квантовая теория гравитации остается предметом активных дискуссий среди специалистов в данной области.

Источники и иллюстрации
Интересные факты
-
Петлевая квантовая теория гравитации (LQG) — это одна из самых перспективных теорий квантовой гравитации, которая пытается объединить общую теорию относительности с квантовой механикой. LQG утверждает, что пространство и время состоят из крошечных дискретных петель, называемых спиновыми сетями, которые являются квантовыми объектами.
-
LQG имеет ряд преимуществ перед другими теориями квантовой гравитации. Во-первых, она не требует введения дополнительных измерений, как это делают некоторые другие теории. Во-вторых, она совместима с общей теорией относительности в классическом пределе, что означает, что она может объяснить все наблюдаемые явления в гравитации.
-
LQG все еще находится в стадии разработки, и есть ряд проблем, которые необходимо решить, прежде чем она сможет стать полной теорией квантовой гравитации. Одна из основных проблем заключается в том, что LQG очень сложна для математического описания, и пока не существует способа точно решить уравнения теории.

Литература
- Three Roads to Quantum Gravity. Lee Smolin. Basic Books, 2001.
- The Quantum of Area? John Baez. Nature, vol.421, pp. 702-703; February 2003.
- How Far Are We from the Quantum Theory of Gravity? Lee Smolin. March 2003. Препринт
- Welcome to Quantum Gravity. Special Section, Physics World, Vol.16, No.11, pp. 27-50; November 2003.
- Loop Quantum Gravity. Lee Smolin.
Опыт других людей
Петлевая квантовая теория гравитации вызывает большой интерес у научного сообщества и общественности. Многие ученые высказывают свое мнение по этому поводу. Одни считают, что это перспективное направление, способное объединить классическую гравитацию с квантовой механикой. Другие высказывают сомнения и указывают на сложность экспериментальной проверки этой теории. Однако, все согласны в том, что развитие квантовой теории гравитации имеет важное значение для понимания фундаментальных законов природы.

Примечания
|
п Теории гравитации |
|||
| Стандартные теории гравитации | Альтернативные теории гравитации | Квантовые теории гравитации | Единые теории поля |
|---|---|---|---|
Классическая физика
Принципы
|
Классические
Релятивистские
|
||
Петлевая квантовая гравитация — что это такое? Именно этот вопрос мы рассмотрим в данной статье. Для начала определим ее характеристику и фактические сведения, а далее ознакомимся с ее оппонентом — теорией струн, которую мы рассмотрим в общем виде для осмысления и взаимосвязи с петлевой квантовой гравитацией.
Введение
Одной из теорий, описывающих квантовую гравитацию, является набор данных о петлевой гравитации на квантовом уровне организации Вселенной. Данные теории основываются на концепции дискретности, как времени, так и пространства в масштабах Планка. Позволяет реализоваться гипотезе пульсирующей Вселенной.
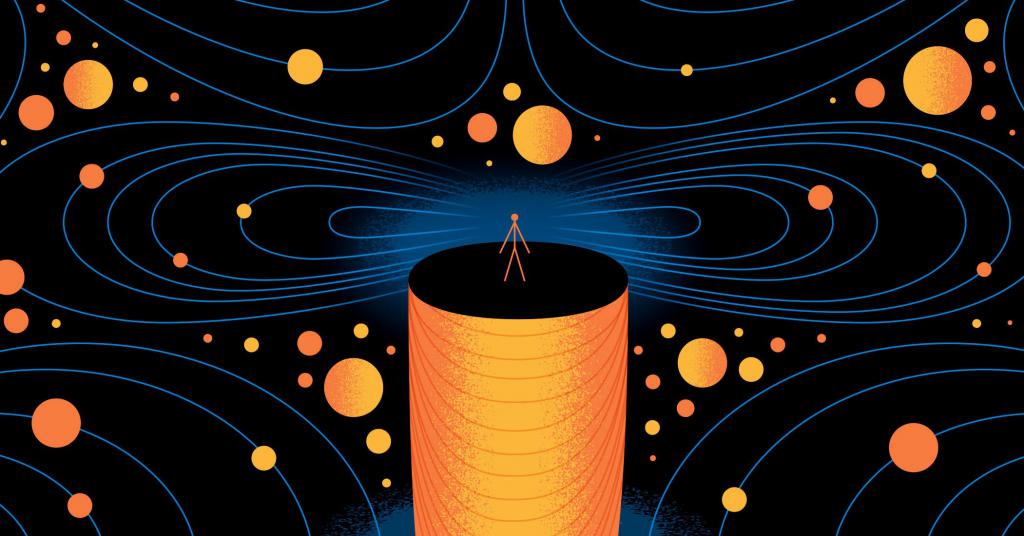
Ли Смолин, Т. Джекобсон, К. Ровелли, и А. Аштекар являются основателями теории петлевой квантовой гравитации. Начало ее формирования приходится на 80-е гг. ХХ века. В соответствии с утверждениями данной теории, «ресурсы» — время и пространство — это системы из дискретных фрагментов. Они описываются как ячейки размером с кванты, которые скрепляются между собой особым способом. Однако, доходя до больших размеров, мы наблюдаем сглаживание пространства-времени, и оно нам кажется непрерывным.
Петлевая гравитация и частички мироздания
Одной из самых ярких «особенностей» теории петлевой квантовой гравитации является ее естественная способность решения некоторых проблем физики. Она позволяет объяснять немало вопросов, связанных со стандартной моделью физики элементарных частичек.
В 2005 году вышла статья С. Бильсона-Томпсона, который предлагал в ней модель с трансформированным ришоном Харари, который принял вид протяженного ленточного объекта. Последний называют риббоном. Оценивающийся потенциал говорит о том, что она могла бы объяснить причину самостоятельной организации всех субкомпонентов. Ведь именно это явление вызывает цветовой заряд. Предыдущая преонная модель для себя считала базовым элементом точечные частицы. Заряд цвета поддавался постулированию. Эта модель позволяет описывать электрические заряды как топологическую сущность, что способна возникнуть в случае перекручивания риббонов.
Вторая статья этих соавторов, выпущенная в 2006 г., является трудом, в котором также принимали участие Л. Смолин и Ф. Маркополу. Ученые выдвинули предположение о том, что все теории квантовой петлевой гравитации, входящие в класс петлевых, утверждают: в них пространство и время — это возбужденные квантованием состояния. Эти состояния могут выполнять роли преонов, которые приводят к появлению известной стандартной модели. Ею в свою очередь обуславливается эмергентность свойств теории.
Четверо ученых также выдвинули предположение о том, что теория квантовой петлевой гравитации способна воспроизводить Стандартную модель. Она автоматическим способом взаимно связывает четыре фундаментальные силы. В таком виде, под понятием «брэд» (переплетенное волокнистое пространство-время), здесь подразумевается понятие преонов. Именно брэды дают возможность воссоздать верную модель из представителей «первого поколения» частиц, что основана на фермионах (кварках и лептонах) с преимущественно правильными способами воссоздания заряда и четности собственно самих фермионов.
Бильсон-Томпсон предполагал, что фермионы из фундаментального «ряда» 2-го и 3-го поколений могут представляться в виде тех же брэдов, но с более сложной структурой. Фермионы 1-го поколения здесь представлены простейшими брэдами. Однако здесь важно знать, что конкретные представления о сложности их устройства еще не выдвигались. Полагается, что заряды цветового и электрического типов, а также «статус» четности частичек у первого поколения, формируются точно таким же образом, как и у других. После того, как эти частицы были открыты, было совершено множество опытов по созданию воздействий квантовыми флуктуациями на них. Конечные результаты экспериментов показали, что эти частички являются устойчивыми и не распадаются.
Ленточная структура
Так как здесь мы рассматриваем информацию о теориях без использования расчетов, то можно сказать, что это петлевая квантовая гравитация «для чайников». И она не может обойтись без описания ленточных структур.
Сущности, в которых материя представлена тем же «веществом», что и пространство-время, являются общим описательным представлением модели, которую нам представили Бильсон-Томпсон. Эти сущности являются ленточными структурами данной описательной характеристики. Эта модель показывает нам, как происходит получение фермионов и как образуются бозоны. Однако она не дает ответа на вопрос о том, каким образом можно получить бозон Хигса с применением брэндинга.
Л. Фрейделем, Дж. Ковальским-Гликманом и А. Стародубцевым в 2006 году в одной статье было высказано предположение о том, что линиями Вильсона гравитационных полей можно описывать элементарные частички. Это подразумевает, что свойства, которыми обладают частички, способны соответствовать качественным параметрам петель Вильсона. Последние в свою очередь являются базовым объектом петлевой квантовой гравитации. Еще эти исследования и расчеты рассматривается в качестве дополнительной базы для теоретической поддержки, описывающей модели Бильсона-Томпсона.
Использование формализма модели спиновой пены, обладающей непосредственным отношением к теории, изучаемой и анализируемой в этой статье (Т.П.К.Г.), а также базирование на исходном ряде принципов этой теории квантовой петлевой гравитации, дает возможность воспроизводить некоторые частички Стандартной модели, которые не могли получить ранее. Это были фотонные частицы, также глюоны и гравитоны.
Существует также модель гелонов, в которой брэды не рассматривают ввиду их отсутствия как таковых. Но сама модель не дает точной возможности отрицать их существование. Ее преимущество заключается в том, что мы можем описывать бозон Хиггса как некую композитную систему. Это объясняется наличием у частиц с большим значением массы более сложных внутренних структур. Учитывая перекручивание брэдов, мы вправе предположить, что данная структура может относиться к механизму создания массы. Например, вид модели Бильсона-Томпсона, описывающий фотон как частицу с нулевой массой, соответствует состоянию брэда в не перекрученном состоянии.
Понимание подхода Бильсона-Томпсона
На лекциях по квантовой петлевой гравитации при описании лучшего подхода к пониманию модели Бильсона-Томпсона упоминают, что это описание преонной модели элементарных частиц позволяет охарактеризовать электроны как функции волновой природы. Дело в том, что общее количество квантовых состояний, которыми обладают спиновые пены с когерентными фазами, также может быть описано с использованием терминов В настоящее время происходят активные работы, направленные на объединение теории элементарных частичек и Т.П.К.Г.
Среди книг по петлевой квантовой гравитации найти множество информации можно, например, в трудах О. Фейрина о парадоксах квантового мира. Среди других работ стоит уделить внимание статьям Ли Смолина.
Проблематика
Статья в модифицированной версии от Бильсона-Томпсона признает, что спектр массы частиц является нерешенной проблемой, которую его модель описать не может. Также она не решает вопросы, связанные со спинами, смешиванием Кабиббо. Она требует привязки к более фундаментальной теории. Более поздние варианты статьи прибегают к описанию динамики брэдов при помощи перехода Пачнера.
В мире физики происходит постоянное противоборство: теория струн vs теория петлевой квантовой гравитации. Это два фундаментальных труда, над которыми работали и работают множество известных ученых всего мира.
Теория струн
Говоря о теории квантовой петлевой гравитации и теории струн, важно понимать, что это два абсолютно разных способа осознания устройства материи и энергии во Вселенной.
Теория струн — это «путь эволюции» физической науки, который старается изучить динамику взаимных действий не между точечными частицами, а квантовыми струнами. Материал теории сочетает в себе идею механики квантового мира и теорию относительности. Это, вероятно, поможет человеку построить будущую теорию квантовой гравитации. Именно ввиду формы объекта изучения эта теория старается другим способом описать основы Вселенной.
В отличие от теории квантовой петлевой гравитации, теория струн и ее основы базируются на гипотетических данных, предполагающих, что любая элементарная частица и все ее взаимодействия фундаментального характера являются следствием колебаний квантовых струн. Эти «элементы» Вселенной обладают ультрамикроскопическими размерами и в масштабах порядка длинны Планка равны 10 -35 м.
Данные этой теории являются математически осмысленными довольно точно, однако найти фактические подтверждения в области экспериментов она еще не смогла. Теория струн связана с мультивселенными, которые являются интерпретацией информации в бесконечном количестве миров с разным видом и формой развития абсолютно всего.
Основа
Петлевая квантовая гравитация или Это довольно важный вопрос, который сложно, но нужно осмыслить. Особенно это важно для физиков. Чтобы лучше понять теорию струн, важно будет кое-что знать.
Теория струн могла бы нам представить описание перехода и всех особенностей каждой фундаментальной частицы, однако это возможно лишь в том случае, если бы мы также могли экстраполировать струны в низкоэнергетическую область физики. В подобном случае все эти частички принимали бы вид ограничений на спектр возбуждения в нелокальном одномерном объективе, которых безграничное множество. Характерной размерностью струн является крайне малое значение (порядка 10 -33 м). Ввиду этого человек не способен наблюдать их в ходе экспериментов. Аналог данного явления — это струнное колебание музыкальных инструментов. Спектральные данные, которые «образуют» струну, возможными могут быть лишь для определенной частоты. С увеличением частоты растет и энергия (накопленная от колебаний). Если применить к этому утверждению формулу E = mc 2 , то можно создать описание материи, из которой состоит Вселенная. Теория постулирует, что размеры массы частицы, которые проявляют себя в виде колеблющейся струны, наблюдаются в реальном мире.
Струнная физика оставляет открытым вопрос о размерностях пространства-времени. Отсутствие дополнительных пространственных измерений в макроскопическом мире объясняется двумя путями:
- Компактификацией измерений, которые скручиваются до размеров, в которых они будут соответствовать порядку планковской длины;
- Локализацией всего количества частиц, которые образуют многомерную Вселенную на четырехмерном «листе Мира», который описывают как мультивселенную.
Квантование
В этой статье рассмотрено понятие теории петлевой квантовой гравитации для чайников. Данная тема является крайне сложной для осмысления на математическом уровне. Здесь же мы рассматриваем общее представление на основе описательного подхода. Причем по отношению к двум «противостоящим» теориям.
Чтобы осмыслить теорию струн лучше, также важно знать о существовании подхода первичного и вторичного квантования.
Вторичное квантование основывается на понятиях струнного поля, а именно на функционале для пространства петель, что похоже на квантовую теорию поля. Формализмы первичного подхода посредством математических приемов создают описание движения пробных струн в их внешних полях. Это не сказывается отрицательным образом на взаимодействии между струнами, а также включает в себя явление распада и объединения струн. Первичный подход — это связующее звено между струнными теориями и утверждениями обычной теорией полей на мировой поверхности.
Суперсимметрия
Самым важным и обязательным, а также реалистичным «элементом» теории струн является суперсимметрия. Общий набор частичек и взаимодействия между ними, которые наблюдаются при относительно низких энергиях, способен воспроизвести структурную составную стандартной модели практически во всем виде. Множество свойств стандартной модели приобретает изящные объяснения в раках суперструнной теории, что также является важным аргументом для теории. Однако еще не существует принципов, которые могли бы объяснить то или иное ограничение струнных теорий. Эти постулаты должны позволять получать форму мира, подобную стандартной модели.
Свойства
Самыми важными свойствами струнной теории являются следующие:
- Принципы, обуславливающие устройство Вселенной — это гравитация и механика квантового мира. Они являются компонентами, которые нельзя разделять при создании общей теории. Теория струн реализует данное предположение.
- Исследования множества развитых концепций ХХ века, которые позволяют нам понимать фундаментальное устройство мира, всем множеством своих принципов работы и объяснения, объединяются и вытекают из теории струн.
- Теория струн не обладает свободными параметрами, которые необходимо подгонять для обеспечения согласия, как, например, это требуется в стандартной модели.
В заключение
Говоря простым языком, квантовая петлевая гравитация — это один из способов восприятия реальности, который старается описать фундаментальное устройство мира на уровне элементарных частиц. Она позволяет решать множество проблем физики, которые затрагивают вопросы организации материи, а также относится к одной из ведущих теорий во всем мире. Ее главным оппонентом является теория струн, что вполне логично, учитывая множество верных утверждений последней. Обе теории находят свое подтверждение в различных областях исследования элементарных частиц, а попытки объединить «квантовый мир» и гравитацию по сей день продолжаются.
Относится к «Теории мироздания»
Теория петлевой квантовой гравитации
Что было до Большого взрыва и откуда взялось время?
В теор
ии квантовой
гравитации привычное нам гладкое и непрерывное
пространство на сверхмалых масштабах оказывается
структурой с очень сложной геометрией
(изображение с сайта www.aei.mpg.de)
Вопросы, вынесенные в заголовок, обычно физиками не
обсуждаются, поскольку общепринятой теор
ии, способной на них
ответить, пока нет. Однако недавно в рамках петлевой квантовой
гравитации всё же удалось проследить эволюцию упрощенной модели
Вселенной назад во времени, вплоть до момента Большого взрыва, и
даже заглянуть за него. Попутно выяснилось, как именно в этой модели
возникает время.
Наблюдения за Вселенной показывают, что и на самых больших
масштабах она вовсе не неподвижна, а эволюционирует с течением времени . Если на основе
современных теор
ий проследить эту эволюцию назад во времени, то
окажется, что наблюдаемая ныне часть Вселенной была раньше горячее и
компактнее, чем сейчас, а начало ей дал Большой
взрыв — некий процесс возникновения Вселенной из
сингулярности: особой ситуации, для которой современные законы
физики неприменимы.
Физиков такое положение вещей не устраивает: им хочется понять и
сам процессБольшого взрыва. Именно поэтому сейчас
предпринимаются многочисленные попытки построить теор
ию, которая
была бы применима и к этой ситуации. Поскольку в первые мгновения
после Большого взрыва самой главной силой была гравитация,
считается, что достичь этой цели возможно только в рамках
непостроенной пока
квантовой теор
ии гравитации.
Одно время физики надеялись, что квантовая гравитация будет
описана с помощью теор
ии суперструн , но недавний
кризис суперструнных теор
ий поколебал эту уверенность. В такой
ситуации больше внимания стали привлекать иные подходы к описанию
квантовогравитационных явлений, и в частности,
петлевая квантовая
гравитации.
Именно в рамках петлевой квантовой гравитации недавно был получен
очень впечатляющий результат. Оказывается, из-за квантовых эффектов
начальная сингулярность исчезает. Большой взрыв перестает
быть особой точкой, и удается не только проследить его протекание,
но и заглянуть в то, что было до Большого взрыва. Краткое описание
этих результатов было недавно опубликовано в статье
A. Ashtekar, T. Pawlowski, P. Singh, Physical Review Letters, 96, 141301
(12 April 2006) , доступной также как gr-qc/0602086 , а их подробный вывод изложен в
вышедшем на днях препринте этих же авторов gr-qc/0604013 .
Петлевая квантовая гравитация принципиально отличается от обычных
физических теор
ий и даже от теор
ии суперструн. Объектами теор
ии
суперструн, к примеру, являются разнообразные струны и многомерные
мембраны, которые, однако, летают в
заранее приготовленномдля них пространстве и времени. Вопрос о том, как именно возникло
это многомерное пространство-время, в такой теор
ии не решишь.
В петлевой теор
ии гравитации главные объекты — маленькие квантовые ячейки пространства , определенным
способом соединенные друг с другом. Законом их соединения и их
состоянием управляет некоторое поле, которое в них существует.
Величина этого поля является для этих ячеек неким «
внутренним
временем»: переход от слабого поля к более сильному полю
выглядит совершенно так, как если бы было некое «прошлое», которое
бы влияло на некое «будущее». Закон этот устроен так, что для
достаточно большой вселенной с малой концентрацией энерги
и (то есть
далеко от сингулярности) ячейки как бы «сплавляются» друг с другом,
образуя привычное нам «сплошное» пространство-время.
Авторы статьи утверждают, что всего этого уже достаточно, чтобы
решить задачу о том, что происходит со Вселенной при приближении к
сингулярности. Решения полученных ими уравнений показали, что при
экстремальном «сжатии» вселенной пространство «рассыпается»,
квантовая геометрия не позволяет уменьшить его объем до нуля,
неизбежно происходит остановка и вновь начинается расширение. Эту
последовательность состояний можно отследить как вперед, так и назад
во «времени», а значит, в этой теор
ии до Большого взрыва с
неизбежностью присутствует «Большой хлопок» — коллапс
«предыдущей» вселенной. При этом свойства этой предыдущей вселенной
не теряются в процессе коллапса, а однозначно передаются в нашу
Вселенную.
Описанные вычисления опираются, правда, на некоторые упрощающие
предположения о свойствах универсального поля. По-видимому, общие
выводы сохранятся и без таких предположений, но это еще нуждается в
проверке. Будет крайне интересно проследить за дальнейшим развитием
этих идей.
Атомы пространства и времени
© Ли Смолин
«В мире науки», апрель 2004
Ли Смолин
Если удивительная теор
ия петлевой квантовой гравитации
верна, то пространство и время, воспринимаемые нами как непрерывные, на самом
деле состоят из дискретных частиц.
С древних времен некоторые философы и ученые предполагали, что
материя может состоять из крошечных атомов, но еще 200 лет назад мало кто верил,
что их существование можно доказать. Сегодня мы наблюдаем отдельные атомы и
изучаем частицы, их составляющие. Зернистое строение вещества для нас уже не
новость.
В последние десятилетия физики и математики задаются
вопросом: не из дискретных ли частей состоит пространство? Действительно ли оно
непрерывно или больше похоже на кусок ткани, сотканной из отдельных волокон?
Если бы мы могли наблюдать чрезвычайно малые объекты, то увидели бы атомы
пространства, неделимые мельчайшие частицы объема? А как быть со временем:
плавно ли происходят изменения в природе или мир развивается крошечными
скачками, действуя словно компьютер?
За последние 16 лет ученые
заметно приблизились к ответам на эти вопросы. Согласно теор
ии со странным
названием «петлевая квантовая гравитация», пространство и время действительно
состоят из дискретных частей. Расчеты, выполненные в рамках этой концепции,
описывают простую и красивую картину, которая помогает нам объяснить загадочные
явления, относящиеся к черным дырам и Большому взрыву. Но главное достоинство
упомянутой теор
ии заключается в том, что уже в ближайшем будущем ее предсказания
можно будет проверить экспериментально: мы обнаружим атомы пространства, если
они действительно существуют.
Кванты
Вместе с моими коллегами мы развивали теор
ию петлевой квантовой
гравитации (ПКГ), пытаясь разработать долгожданную квантовую теор
ию тяготения.
Чтобы объяснить исключительную важность последней и ее отношение к дискретности
пространства и времени, я должен немного рассказать о квантовой теор
ии и теор
ии
гравитации.
Появление квантовой механики в первой четверти XX в. было
связано с доказательством, что материя состоит из атомов. Квантовые уравнения
требуют, чтобы некоторые величины, такие как энерги
я атома, могли принимать
только определенные дискретные значения. Квантовая механика в точности описывает
свойства и поведение атомов, элементарных частиц и связывающих их сил. Самая
успешная в истории науки квантовая теор
ия лежит в основе нашего понимания химии,
атомной и субатомной физики, электроники и даже биологии.
В те же
десятилетия, когда зарождалась квантовая механика, Альберт Эйнштейн разработал
общую теор
ию относительности, которая представляет собой теор
ию гравитации.
Согласно ей, сила тяготения возникает в результате изгиба пространства и времени
(которые вместе образуют пространство-время) под действием материи.
Представьте себе тяжелый шар, помещенный на
резиновый лист, и маленький шарик, который катается вблизи большого. Шары можно
рассматривать как Солнце и Землю, а лист — как пространство. Тяжелый шар создает
в резиновом полотне углубление, по склону которого меньший шарик скатывается к
большему, как будто некоторая сила — гравитатация — тянет его в этом
направлении. Точно так же любая материя или сгусток энерги
и искажают геометрию
пространства-времени, притягивая частицы и световые лучи; это явление мы и
называем гравитацией.
По отдельности квантовая механика и общая теор
ия
относительности Эйнштейна экспериментально подтверждены. Однако еще ни разу не
исследовался случай, когда можно было бы проверить обе теор
ии одновременно. Дело
в том, что квантовые эффекты заметны лишь в малых масштабах, а для того, чтобы
стали заметны эффекты общей теор
ии относительности, требуются большие массы.
Объединить оба условия можно лишь при каких-то экстраординарных
обстоятельствах.
Помимо отсутствия экспериментальных данных существует
огромная концептуальная проблема: общая теор
ия относительности Эйнштейна
полностью классическая, т.е. неквантовая. Для обеспечения логической целостности
физики нужна квантовая теор
ия гравитации, объединяющая квантовую механику с
общей теор
ией относительности в квантовую теор
ию пространства-времени.
Физики разработали множество математических процедур для превращения
классической теор
ии в квантовую. Многие ученые тщетно пытались применить их к
общей теор
ии относительности.
Расчеты, проведенные в 1960-х и 1970-х
гг., свидетельствовали о том, что квантовую механику и общую теор
ию
относительности объединить невозможно. Казалось, ситуацию может спасти только
введение совершенно новых постул
атов, дополнительных частиц, полей или объектов
иного рода. Экзотика единой теор
ии должна проявляться только в тех
исключительных случаях, когда существенными становятся и квантово-механические,
и гравитационные эффекты. В попытках достижения компромисса родились такие
направления, как теор
ия твисторов, некоммутативная геометрия и
супергравитация.
Большой популярностью у физиков пользуется теор
ия
струн, согласно которой помимо трех хорошо известных пространственных измерений
есть еще шесть или семь, которые до сих пор никому не удавалось заметить. Теория
струн также предсказывает существование множества новых элементарных частиц и
сил, наличие которых еще ни разу не было подтверждено наблюдениями. Некоторые
ученые полагают, что она является частью так называемой М-теор
ии, но, к
сожалению, никакого точного ее определения пока предложено не было. Поэтому
многие специалисты убеждены, что следует изучить имеющиеся альтернативы. Наша
петлевая квантовая теор
ия гравитации — наиболее развитая из них.
Большая лазейка
В середине 1980-х гг. мы вместе с Аби Аштекером (Abhay
Ashtekar), Тэдом Джекобсоном (Ted Jacobson) и Карло Ровелли (Carlo Rovelli)
решили еще раз попытаться объединить квантовую механику и общую теор
ию
относительности с помощью стандартных методов. Дело в том, что в отрицательных
результатах, полученных в 1970-х гг., оставалась важная лазейка: при расчетах
предполагалось, что геометрия пространства непрерывная и гладкая независимо от
того, насколько детально мы исследуем ее. Точно также люди рассматривали
вещество до открытия атомов.
Итак, мы решили отказаться от концепции
гладкого непрерывного пространства и не вводить никаких гипотез
, кроме хорошо
проверенных экспериментально положений общей теор
ии относительности и квантовой
механики. В частности, в основе наших расчетов были заложены два ключевых
принципа теор
ии Эйнштейна.
Первый из них — независимость от окружения
— провозглашает, что геометрия пространства-времени не фиксирована, а является
меняющейся, динамической величиной. Чтобы определить геометрию, необходимо
решить ряд уравнений, учитывающих влияние вещества и энерги
и. Кстати,
современная теор
ия струн не является независимой от окружения: уравнения,
описывающие струны, сформулированы в определенном классическом (т.е.
неквантовом) пространстве-времени.
Второй принцип, названный
«диффеоморфной инвариантностью», гласит, что для отображения
пространства-времени и построения уравнений мы вольны выбирать любую систему
координат. Точка в пространстве-времени задается только физически происходящими
в ней событиями, а не ее положением в какой-то особой системе координат (не
существует никаких особых координат). Диффеоморфная инвариантность — чрезвычайно
важное фундаментальное положение общей теор
ии относительности.
Аккуратно объединив оба принципа со стандартными методами квантовой механики, мы
разработали математический язык, который позволил провести нужные вычисления и
выяснить, дискретно пространство или непрерывно. К нашему восторгу, из расчетов
следовало, что пространство квантовано! Так мы заложили основу теор
ии петлевой
квантовой гравитации. Кстати, термин «петлевая» был введен из-за того, что в
некоторых вычислениях использовались маленькие петли, выделенные в
пространстве-времени.
Многие физики и математики проверили наши
расчеты с использованием различных методов. За прошедшие годы теор
ия петлевой
квантовой гравитации окрепла благодаря усилиям ученых разных стран мира.
Проделанная работа позволяет нам доверять той картине пространства-времени,
которую я опишу ниже.
В нашей квантовой теор
ии речь идет о структуре
пространства-времени в самых малых масштабах, и чтобы разобраться в ней,
необходимо рассматривать ее предсказания для маленькой площади или объема. Имея
дело с квантовой физикой, важно определить, какие физические величины должны
быть измерены. Представьте себе некую область, обозначенную границей В (см.
рис. внизу), которая может быть задана материальным объектом (например,
чугунной скорлупой) или непосредственно геометрией пространства-времени
(например, горизонтом событий в случае черной дыры). Что происходит, когда мы
измеряем объем описанной области? Каковы возможные результаты, допускаемые как
квантовой теор
ией, так и диффеоморфной инвариантностью? Если геометрия
пространства непрерывна, то рассматриваемая область может иметь любой размер, и
ее объем может быть выражен любым действительным положительным числом, в
частности, сколь угодно близким к нулю. Но если геометрия гранулированa, то
результат измерения может принадлежать только дискретному набору чисел и не
может быть меньше некоторого минимально возможного объема. Давайте вспомним,
какой энерги
ей может обладать электрон, обращающийся вокруг атомного ядра? В
рамках классической физики — любой, но квантовая механика
допускает только определенные, строго фиксированные дискретные значения энерги
и.
Различие такое же, как между измерением объема жидкости, образующей непрерывный
поток (с точки зрения ученых XVIII в.), и определением количества воды, атомы
которой можно сосчитать.
Согласно теор
ии петлевой квантовой
гравитации, пространство подобно атомам: числа, получаемые при измерении объема,
образуют дискретный набор, т.е. объем изменяется отдельными порциями. Другая
величина, которую можно измерить, — площадь границы В, которая тоже оказывается
дискретной. Иными словами, пространство не непрерывно и состоит из определенных
квантовых единиц площади и объема.
Возможные значения объема и площади
измеряются в единицах, производных от длины Планка, которая связана с силой
гравитации, величиной квантов и скоростью света. Длина Планка очень мала:
10 -33 см; она определяет масштаб, при котором геометрию пространства
уже нельзя считать непрерывной. Самая маленькая возможная площадь, отличная от
нуля, примерно равна квадрату длины Планка или 10 -66 см 2 .
Наименьший возможный объем, отличный от нуля, — куб длины Планка или
10 -99 см 3 . Таким образом, согласно теор
ии в каждом
кубическом сантиметре пространства содержится приблизительно 10 99
атомов объема. Квант объема настолько мал, что в кубическом сантиметре таких
квантов больше, чем кубических сантиметров в видимой Вселенной
(10 85).
Спиновые сети
На что же похожи кванты объема и площади? Быть может, пространство
состоит из огромного количества крошечных кубов или сфер? Нет, не все так
просто. Квантовые состояния объема и площади мы изображаем в виде диаграмм,
которые не лишены своеобразной красоты. Вообразите область пространства, по
форме напоминающую куб (см.
рис. внизу
). На диаграмме мы изображаем ее как точку, представляющую объем, с
шестью выходящими из нее линиями, каждая из которых изображает одну из граней
куба. Число рядом с точкой указывает величину объема, а числа рядом с линиями —
величину площади соответствующих граней.
Поместим на вершину куба
пирамиду. У наших многогранников есть общая грань, и их следует изобразить как
две точки (два объема), соединенные одной из линий (грань, которая соединяет
объемы). У куба осталось пять свободных граней (пять линий), а у пирамиды —
четыре (четыре линии). Аналогично можно изобразить любые комбинации различных
многогранников: объемные полиэдры становятся точками или узлами, а плоские грани
— линиями, соединяющими узлы. Математики называют такие диаграммы
графами.
В нашей теор
ии мы отбрасываем рисунки многогранников и
оставляем только графы. Математика, описывающая квантовые состояния объема и
площади, обеспечивает нас набором правил, указывающих, как линии могут соединять
узлы и какие числа могут располагаться в различных местах диаграммы. Каждое
квантовое состояние соответствует одному из графов, и каждому графу,
удовлетворяющему правилам, соответствует квантовое состояние. Графы представляют
собой удобную краткую запись возможных квантовых состояний
пространства.
Диаграммы гораздо больше подходят для представления
квантовых состояний, чем многогранники. В частности, некоторые графы соединяются
такими странными способами, что их невозможно аккуратно преобразовать в картину
из полиэдров. Например, в тех случаях, когда пространство изогнуто, невозможно
изобразить многогранники, стыкующиеся должным образом, зато совсем не трудно
нарисовать граф и по нему вычислить, насколько искажено пространство. Поскольку
именно искажение пространства создает гравитацию, диаграммы играют огромную роль
в квантовой теор
ии тяготения.
Для простоты мы часто рисуем графы в
двух измерениях, но лучше представлять их заполняющими трехмерное пространство,
потому что именно его они изображают. Но здесь есть концептуальная ловушка:
линии и узлы графа не занимают конкретные положения в пространстве. Каждый граф
определяется только тем, как его части соединяются между собой и как они
соотносятся с четко заданными границами (например, с границей области B). Однако
нет никакого непрерывного трехмерного пространства, в котором, как может
показаться, размещаются графы. Линии и узлы — это и есть пространство, геометрия
которого определяется тем, как они соединяются.
Описанные графы
называются спиновыми сетями, потому что указанные на них числа связаны со
спином. Еще в начале 1970-х гг. Роджер Пенроуз
(Roger Penrose) из Оксфордского
университета предположил, что спиновые сети имеют отношение к теор
ии квантовой
гравитации. В 1994 г. наши точные вычисления подтвердили его интуитивную
догадку. Читатели, знакомые с диаграммами Фейнмана, должны обратить внимание,
что спиновые сети ими не являются, несмотря на внешнее сходство. Диаграммы
Фейнмана отражают квантовые взаимодействия между частицами, переходящими из
одного квантового состояния в другое. Спиновые сети олицетворяют фиксированные
квантовые состояния объемов и площадей пространства.
Отдельные узлы и
ребра диаграмм представляют собой чрезвычайно малые области пространства:
типичный узел соответствует объему около одной длины Планка в кубе, а линия —
площади порядка одной длины Планка в квадрате. Но, в принципе, спиновая сеть
может быть неограниченно большой и сколь угодно сложной. Если бы мы могли
изобразить детальную картину квантового состояния нашей Вселенной (т.е.
геометрию ее пространства, искривленного и перекрученного тяготением галактик,
черных дыр и пр.), то получилась бы гигантская спиновая сеть невообразимой
сложности, содержащая приблизительно 10 184 узлов.
Итак,
спиновые сети описывают геометрию пространства. Но что можно сказать о материи и
энерги
и, находящихся в нем? Частицы, такие как электроны, соответствуют
определенным узлам, снабженным дополнительными метками. Поля, такие как
электромагнитное, обозначаются аналогичными маркерами на линиях графа. Движение
частиц и полей в пространстве представляет собой дискретное (скачкообразное)
перемещение меток по графу.
Шаги и пена
Частицы и поля — не единственные движущиеся объекты. Согласно общей
теор
ии относительности, при перемещении материи и энерги
и пространство
модифицируется, по нему даже могут проходить волны, подобно ряби на озере. В
теор
ии петлевой квантовой гравитации такие процессы изображаются дискретными
трансформациями спиновой сети, при которых шаг за шагом изменяется связность
графов (см.
рис. внизу).
При описании квантово-механических явлений физики
вычисляют вероятность различных процессов. Мы делаем то же самое, когда
применяем теор
ию петлевой квантовой гравитации, чтобы описать изменение
геометрии пространства или движение частиц и полей в спиновой сети. Томас Тиманн
(Thomas Thiemann) из Института теор
етической физики в Ватерлоо вывел точные
выражения для вычисления квантовой вероятности шагов спиновой сети. В результате
появилась четкая процедура для вычисления вероятности любого процесса, который
может происходить в мире, подчиняющемся правилам нашей, теперь уже окончательно
сформировавшейся теор
ии. Остается только вычислять и делать предсказания о том,
что можно будет наблюдать в тех или иных экспериментах.
В теор
ии
относительности пространство и время неотделимы и представляют собой единое
пространство-время. При введении концепции пространства-времени в теор
ию
петлевой квантовой гравитации спиновые сети, представляющие пространство,
превращаются в так называемую спиновую пену. С добавлением еще одного измерения
— времени — линии спиновой сети расширяются и становятся двумерными
поверхностями, а узлы растягиваются в линии. Переходы, при которых происходит
изменение спиновой сети (шаги, описанные выше), теперь представлены узлами, в
которых сходятся линии пены. Взгляд на пространство-время как на спиновую пену
был предложен несколькими исследователями, в том числе Карло Ровелли (Carlo
Rovelli), Майком Рейзенбергером (Mike Reisenberger), Джоном Бэрретом (John
Barrett), Луи Крейном (Louis Crane), Джоном Бейзом (John Baez) и Фотини
Маркопулу (Fotini Markopoulou).
Мгновенный снимок происходящего
подобен поперечному срезу пространства-времени. Аналогичный срез спиновой пены
представляет собой спиновую сеть. Однако не стоит заблуждаться, что плоскость
среза перемещается непрерывно подобно плавному потоку времени. Также как
пространство определяется дискретной геометрией спиновой сети, время задается
последовательностью отдельных шагов, которые перестраивают сеть (см. рис. на
стр. 55). Таким образом, время тоже дискретно. Время не течет, как река, а
тикает, как часы. Интервал между «тиками» примерно равен времени Планка, или
10 -43 с. Точнее говоря, время в нашей Вселенной отмеряют мириады
часов: там, где в спиновой пене происходит квантовый шаг, часы делают один
«тик».
Предсказания и проверки
Теория петлевой квантовой гравитации описывает пространство и
время в масштабе Планка, который слишком мал для нас. Так как же нам проверить
ее? Во-первых, очень важно выяснить, можно ли вывести классическую общую теор
ию
относительности как приближение к петлевой квантовой гравитации. Другими
словами, если спиновые сети подобны нитям, из которых соткана ткань, то вопрос
стоит так: удастся ли правильно вычислить упругие свойства куска материала путем
усреднения по тысячам нитей. Получим ли мы описание «гладкой ткани»
классического эйнштейновского пространства, если усредним спиновую сеть по
многим длинам Планка? Недавно ученые успешно решили эту сложнейшую задачу для
нескольких частных случаев, так сказать, для некоторых конфигураций материала.
Например, низкочастотные гравитационные волны, распространяющиеся в плоском
(неизогнутом) пространстве, можно рассматривать как возбуждение определенных
квантовых состояний, описанных в соответствии с теор
ией петлевой квантовой
гравитации.
Хорошей проверкой для петлевой квантовой гравитации оказалась
одна из давнишних загадок о термодинамике черных дыр, и в особенности об их
энтропии. Физики разработали термодинамическую модель черной дыры, опираясь на
гибридную теор
ию, в которой материя рассматривается квантово-механически, а
пространство-время — нет. В частности, в 1970-х гг. Якоб Бекенштейн (Jacob D.
Bekenstein) вывел, что энтропия черной дыры пропорциональна площади ее
поверхности (см. статью «Информация в голографической Вселенной», «В мире
науки», №11, 2003 г.). Вскоре Стивен Хокинг (Stephen Hawking) пришел к выводу,
что черные дыры, особенно маленькие, должны излучать.
Чтобы выполнить
аналогичные вычисления в рамках теор
ии петлевой квантовой гравитации, мы
принимаем границу области В за горизонт событий черной дыры. Анализируя энтропию
соответствующих квантовых состояний, мы получаем в точности предсказание
Бекенштейна. С таким же успехом наша теор
ия не только воспроизводит предсказание
Хокинга об излучении черной дыры, но и позволяет описать его тонкую структуру.
Если когда-либо удастся наблюдать микроскопическую черную дыру, теор
етические
предсказания можно будет проверить, изучая спектр ее излучения.
Вообще
говоря, любая экспериментальная проверка теор
ии петлевой квантовой гравитации
сопряжена с колоссальными техническими трудностями. Характерные эффекты,
описываемые теор
ией, становятся существенными только в масштабе длины Планка,
который на 16 порядков меньше, чем можно будет исследовать в ближайшее время на
самых мощных ускорителях (для исследования меньших масштабов необходима более
высокая энерги
я).
Впрочем, недавно ученые предложили несколько
доступных способов проверки петлевой квантовой гравитации. Длина световой волны,
распространяющейся в среде, претерпевает искажения, что приводит к преломлению и
дисперсии лучей. Аналогичные метаморфозы происходят со светом и частицами,
движущимися через дискретное пространство, описываемое спиновой сетью.
К
сожалению, величина упомянутых эффектов пропорциональна отношению длины Планка к
длине волны. Для видимого света оно не превышает 10 -28 , а для
космических лучей с наибольшей энерги
ей составляет порядка одной миллиардной.
Иными словами, зернистость структуры пространства чрезвычайно слабо сказывается
практически на любом наблюдаемом излучении. Но чем большее расстояние прошел
свет, тем сильнее заметны последствия дискретности спиновой сети. Современная
аппаратура позволяет нам регистрировать излучение гамма-всплесков, расположенных
в миллиардах световых лет (см. статью «Ярчайшие взрывы во Вселенной», «В мире
науки», №4,2003 г.).
Опираясь на теор
ию петлевой квантовой гравитации,
Родольфо Гамбини (Rodolfo Gambini) и Джордж Пуллин (Jorge Pullin) установили,
что фотоны различных энерги
й должны перемещаться с несколько разными скоростями
и достигать наблюдателя в разное время (см.
рис. внизу). Спутниковые наблюдениях гамма-всплесков помогут нам проверить
это. Точность современных приборов в 1 000 раз ниже необходимой, но уже в 2006
г. будет запущена спутниковая обсерватория GLAST, прецизионное оборудование
которой позволит провести долгожданный эксперимент.
Нет ли здесь
противоречия с теор
ией относительности, в которой постул
ируется постоянство
скорости света? Вместе с Джованни Амелино-Камелиа (Giovanni Amelino-Camelia) и
Хояо Магуэйо (Joao Magueijo) мы разработали модифицированные версии теор
ии
Эйнштейна, которые допускают существование фотонов высокой
энерги
и, движущихся с разными скоростями. В свою очередь постоянство
скорости относится к фотонам низких энерги
й, т.е. к длинноволновому
свету.
Другое возможное проявление дискретности пространства-времени
связано с космическими лучами очень высокой энерги
и. Более 30 лет назад ученые
установили, что протоны космических лучей с энерги
ей более 3*10 19 эВ
должны рассеиваться на космическом микроволновом фоне, заполняющем пространство,
и поэтому никогда не достигнут Земли. Тем не менее в японском эксперименте AGASA
было зарегистрировано более 10 событий с космическими лучами даже большей
энерги
и. Оказалось, что дискретность пространства повышает энерги
ю, требуемую
для реакции рассеивания, и позволяет высокоэнергетическим протонам навещать нашу
планету. Если наблюдения японских ученых подтвердятся, а другое объяснение не
будет найдено, то можно будет считать, что дискретность пространства
засвидетельствована экспериментально.
Космос
Теория петлевой квантовой гравитации заставляет нас по-новому
взглянуть на происхождение Вселенной и помогает представить, что происходило
сразу после Большого взрыва. В соответствии с общей теор
ией относительности в
истории мироздания был самый первый, нулевой момент времени, что не согласуется
с квантовой физикой. Расчеты, проведенные Мартином Боджовальдом (Martin
Bojowald) на основании теор
ии петлевой о квантовой гравитации, указывают, что
Большой взрыв фактически был Большим отскоком, так как до него Вселенная быстро
сжималась. Теоретики уже работают над новыми моделями ранней стадии развития
Вселенной, которые вскоре можно будет проверить в космологических наблюдениях.
Не исключено, что нам с вами еще посчастливится узнать, что же происходило до
Большого взрыва.
Не менее серьезно стоит вопрос о космологической
постоянной: положительна или отрицательна плотность энерги
и, пронизывающей
«пустое» пространство? Результаты наблюдения реликтового фона и далеких
сверхновых свидетельствуют о том, что темная энерги
я существует. Более того, она
положительна, поскольку Вселенная расширяется с ускорением. С точки зрения
теор
ии петлевой квантовой гравитации, здесь нет никакого противоречия: еще в
1990 г. Хидео Кодама (Hideo Kodama) составил уравнения, точно описывающие
квантовое состояние Вселенной с положительной космологической
постоянной.
До сих пор еще не решен целый ряд вопросов, в том числе
чисто технических. Какие коррективы следует вносить в частную теор
ию
относительности при чрезвычайно высоких энерги
ях (если вообще следует)? Поможет
ли теор
ия петлевой квантовой гравитации доказать, что различные силы, включая
тяготение, являются аспектами единственного фундаментального
взаимодействия?
Быть может, петлевая квантовая гравитация — это
действительно квантовая общая теор
ия относительности, потому что в ее основе нет
никаких дополнительных предположений, кроме основных принципов квантовой
механики и теор
ии Эйнштейна. Вывод о дискретности пространства-времени,
описываемого спиновой пеной, следует непосредственно из самой теор
ии, а не
вводится как постул
ат.
Однако все, о чем я здесь рассуждал, — это
теор
ия. Возможно, пространство на самом деле гладко и непрерывно в любых, сколь
угодно малых масштабах. Тогда физикам придется ввести дополнительные радикальные
постул
аты, как в случае теор
ии струн. А поскольку в конечном счете все решит
эксперимент, у меня есть хорошие новости — ситуация может проясниться в
ближайшее время.
Дополнительная литература:
Препринт на сайте http://arxiv.org/hep-th/0303185
pp. 27-50; November 2003.
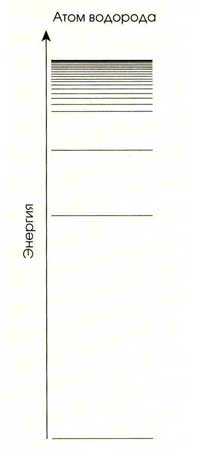
ГЛАВНЫЙ ВЫВОД теор
ии петлевой квантовой гравитации
относится к объемам и площадям. Рассмотрим область пространства, ограниченную
сферической оболочкой В (см. сверху). В соответствии с классической
(неквантовой) физикой ее объем может выражаться любым действительным
положительным числом. Однако, согласно теор
ии петлевой квантовой гравитации,
существует отличный от нуля абсолютный наименьший объем (примерно равный кубу
длины Планка, т.е. 10 99 см 3), а значения больших объемов
представляют собой дискретный ряд чисел. Аналогично, есть ненулевая минимальная
площадь (примерно квадрат длины Планка или 10 66 см 2) и
дискретный ряд допустимых площадей большего размера. Дискретные спектры
допустимых квантовых площадей (слева) и квантовых объемов (в центре) в широком
смысл
е похожи на дискретные квантовые уровни энерги
и атома водорода (справа).
ДИАГРАММЫ, НАЗЫВАЕМЫЕ СПИНОВЫМИ СЕТЯМИ, используются для
представления квантовых состояний пространства при минимальном масштабе длины.
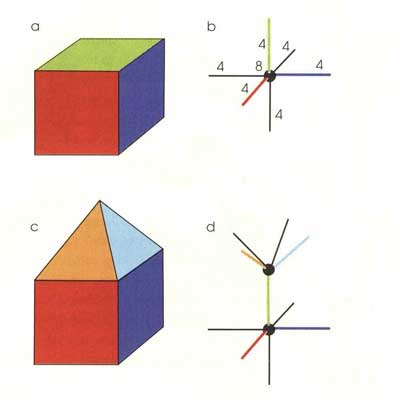
Например, куб (а) — это объем, окруженный шестью квадратными гранями.
Соответствующая спиновая сеть (b) содержит точку (узел), представляющую объем, и
шесть линий, изображающих грани. Число возле узла указывает величину объема, а
число возле линии — площадь соответствующей грани. В рассматриваемом случае
объем равен восьми кубическим единицам Планка, а каждая из граней имеет площадь
в четыре квадратные единицы Планка. (Правила петлевой квантовой гравитации
ограничивают допустимые значения объемов и площадей определенными величинами: у
линий и в узлах могут располагаться лишь определенные комбинации чисел.)
Если
на верхней грани куба помещена пирамида (с), то линия, представляющая эту грань
в спиновой сети, должна соединять узел куба с узлом пирамиды (d). Линии,
соответствующие четырем свободным граням пирамиды и пяти свободным граням куба,
должны выходить из соответствующих узлов. (Для упрощения схемы числа
опущены.)
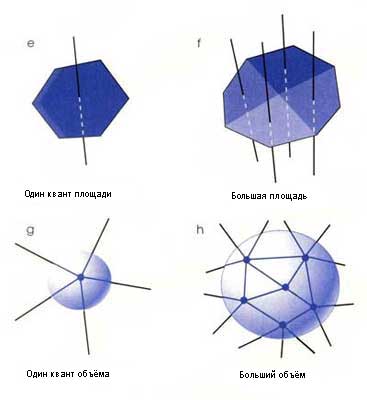
Вообще в спиновой сети один квант площади изображается одной
линией (е), а площадь, составленная из многих квантов, обозначается многими
линиями (f). Аналогично один квант объема изображается одним узлом (g), тогда
как больший объем содержит много узлов (h), Так, объем внутри сферической
оболочки задается суммой всех заключенных в ней узлов, а площадь поверхности
равна сумме всех линий, проходящих сквозь границу области.
Спиновые
сети более фундаментальны, чем конструкции из многогранников: любое сочетание
полиэдров можно изобразить соответствующей диаграммой, но некоторые правильные
спиновые сети представляют такие комбинации объемов и площадей, которые
невозможно составить из многогранников. Такие спиновые сети возникают, когда
пространство искривляется сильным гравитационным полем или квантовыми
флуктуациями геометрии в планковских масштабах.
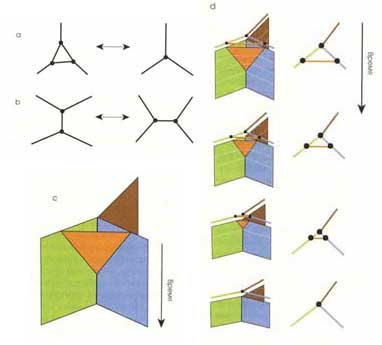
ИЗМЕНЕНИЕ ФОРМЫ пространства при перемещении в нем материи и
энерги
и и при прохождении через него гравитационных волн изображается
дискретными перестройками, шагами спиновой сети. На рис. а связанная группа из
трех квантов объема сливается в один; возможен и обратный процесс. На рис. b два
объема разделяют пространство и соединяются с соседними объемами иным способом.
При изображении в виде полиэдров два многогранника объединяются по их общей
грани, а затем расщепляются, как при раскалывании кристаллов по другой
плоскости. Такие шаги в спиновой сети происходят не только при больших
изменениях геометрии пространства, но и при непрерывных квантовых флуктуациях в
планковском масштабе.
Другой способ изображения шагов заключается в
добавлении к диаграмме еще одной размерности — времени. В результате получается
спиновая пена (с). Линии спиновой сети становятся плоскостями, а узлы
превращаются в линии. Срез спиновой пены в определенный момент времени
представляет собой спиновую сеть. Сделав ряд таких срезов, мы получим кадры
фильма, повествующего о развитии спиновой сети во времени (d). Но обратите
внимание, что эволюция, которая на первый взгляд кажется плавной и непрерывной,
на самом деле идет скачками. Все спиновые сети, содержащие оранжевую линию
(первые три кадра), отображают в точности одну и ту же геометрию пространства,
Длина линий не имеет значения -для геометрии важно лишь то, как соединяются
линии и каким числом отмечена каждая из них. Именно этим и определяется взаимное
расположение и величина квантов объема и площади. Так, на рис, d в течение трех
первых кадров геометрия остается постоянной — 3 кванта объема и 6 квантов
площади. Затем пространство изменяется скачкообразно: остается 1 квант объема и
3 кванта площади, как показано на последнем кадре. Таким образом, время,
определяемое спиновой пеной, изменяется не непрерывно, а последовательностью
внезапных дискретных шагов.
И хотя для наглядности такие
последовательности показаны как кадры фильма, правильнее рассматривать эволюцию
геометрии как дискретное постукивание часов. При одном «тике» оранжевый квант
площади есть; при следующем — он исчез: фактически его исчезновение и определяет
«тик». Интервал между последовательными «тиками» примерно равен времени Планка
(10 -43 с), но между ними время не существует; не может быть никакого
«между», так же как нет воды между двумя соседними молекулами
Н 2 O.
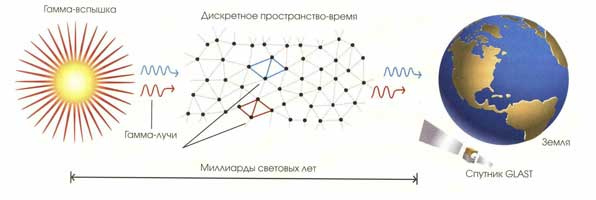
КОГДА В МИЛЛИАРДАХ световых лет от нас происходит
гамма-всплеск, мгновенный взрыв порождает гигантское количество гамма-лучей. В
соответствии с теор
ией петлевой квантовой гравитации фотон, движущийся по
спиновой сети, в каждый момент времени занимает несколько линий, т.е. некоторое
пространство (в реальности на квант света приходится очень много линий, а не
пять, как показано на рисунке). Дискретная природа пространства заставляет
гамма-лучи более высокой энерги
и перемещаться немного быстрее. Разница ничтожна,
но в ходе космического путешествия эффект накапливается миллиардами лет. Если
возникшие при всплеске гамма-лучи разных энерги
й прибывают на Землю в разные
моменты времени, то это свидетельствует в пользу теор
ии петлевой квантовой
гравитации, На 2006 г. запланирован запуск спутника GLAST, на борту которого
будет установлена достаточно чувствительная аппаратура, чтобы обнаружить
дисперсию гамма-излучения.
Пространства определённым способом соединены друг с другом, так что на малых масштабах времени и длины они создают пёструю, дискретную структуру пространства, а на больших масштабах плавно переходят в непрерывное гладкое пространство-время .
Петлевая гравитация и физика элементарных частиц
Одним из преимуществ петлевой квантовой теории гравитации является естественность, с которой в ней получает своё объяснение Стандартная модель физики элементарных частиц.
Таким образом, Бильсон-Томпсон с соавторами предположили, что теория петлевой квантовой гравитации может воспроизвести Стандартную модель, автоматически объединяя все четыре фундаментальных взаимодействия . При этом с помощью преонов, представленных в виде брэдов (переплетений волокнистого пространства-времени) удалось построить успешную модель первого поколения фундаментальных фермионов (кварков и лептонов) с более-менее правильным воспроизведением их зарядов и четностей .
В исходной статье Бильсона-Томпсона предполагалось, что фундаментальные фермионы второго и третьего поколений могут быть представлены в виде более сложных брэдов, а фермионы первого поколения представляются простейшими из возможных брэдов, хотя конкретных представлений сложных брэдов не давалось. Считается, что электрический и цветовой заряды, а также чётность частиц, принадлежащих к поколениям более высокого ранга, должны получаться точно таким же образом, как и для частиц первого поколения.
Использование методов квантовых вычислений позволило показать, что такого рода частицы устойчивы и не распадаются под действием квантовых флуктуаций .
Ленточные структуры в модели Бильсона-Томпсона представлены в виде сущностей, состоящих из той же материи, что и само пространство-время . Хотя в статьях Бильсона-Томпсона и показано, как из этих структур можно получить фермионы и бозоны , вопрос о том, как с помощью брэдинга можно было бы получить бозон Хиггса , в них не обсуждается.
Л. Фрейдель (
L. Freidel), Дж. Ковальский-Гликман (
J. Kowalski-Glikman) и А. Стародубцев в своей статье 2006 года высказали предположение, что элементарные частицы можно представить с помощью линий Вильсона гравитационного поля, подразумевая, что свойства частиц (их массы, энергии и спины) могут соответствовать свойствам петель Вильсона — базовым объектам теории петлевой квантовой гравитации. Эту работу можно рассматривать в качестве дополнительной теоретической поддержки преонной модели Бильсона-Томпсона .
Используя формализм модели
спиновой пены, имеющей непосредственное отношение к теории петлевой квантовой гравитации, и базируясь лишь на исходных принципах последней, можно также воспроизвести и некоторые другие частицы Стандартной модели, такие как фотоны , глюоны и гравитоны — независимо от схемы брэдов Бильсона-Томпсона для фермионов. Однако, по состоянию на 2006 год, с помощью этого формализма пока не удалось построить модели гелонов. В модели гелонов отсутствуют брэды, которые можно было бы использовать для построения бозона Хиггса, но в принципе данная модель не отрицает возможности существования этого бозона в виде некоей композитной системы. Бильсон-Томпсон отмечает, что, поскольку частицы с бо́льшими массами в основном имеют более сложную внутреннюю структуру (учитывая также перекручивание брэдов), то эта структура возможно имеет отношение к механизму формирования массы. Например, в модели Бильсона-Томпсона структура фотона, имеющего нулевую массу, соответствует неперекрученным брэдам. Правда, пока остается неясным, соответствует ли модель фотона, полученная в рамках формализма спиновой пены , фотону Бильсона-Томпсона, который в его модели состоит из трех незакрученных риббонов (возможно, что в рамках формализма спиновой пены можно построить несколько вариантов модели фотона).
Первоначально понятие «преон» использовалось для обозначения точечных субчастиц, входящих в структуру фермионов с половинным спином (лептонов и кварков). Как уже упоминалось, использование точечных частиц приводит к парадоксу массы. В модели Бильсона-Томпсона риббоны не являются «классическими» точечными структурами. Бильсон-Томпсон использует термин «преон» для сохранения преемственности в терминологии, но обозначает с помощью этого термина более широкий класс объектов, являющихся компонентами структуры кварков, лептонов и калибровочных бозонов.
Важным для понимания подхода Бильсона-Томпсона является то, что в его преонной модели элементарные частицы, такие как электрон , описываются в терминах волновых функций. Сумма квантовых состояний спиновой пены, имеющих когерентные фазы, также описывается в терминах волновой функции. Поэтому возможно, что с помощью формализма спиновой пены можно получить волновые функции, соответствующие элементарным частицам (фотонам и электронам). В настоящее время объединение теории элементарных частиц с теорией петлевой квантовой гравитации является весьма активной областью исследований .
В октябре 2006 г. Бильсон-Томпсон модифицировал свою статью , отмечая, что, хотя его модель и была инспирирована преонными моделями, но она не является преонной в строгом смысле этого слова, поэтому топологические диаграммы из его преонной модели скорее всего можно использовать и в других фундаментальных теориях, таких как, например, М-теория . Теоретические ограничения, накладываемые на преонные модели, неприменимы к его модели, поскольку в ней свойства элементарных частиц возникают не из свойств субчастиц, а из связей этих субчастиц друг с другом (брэдов).
Одной из возможностей является, например, «встраивание» преонов в М-теорию или в теорию петлевой квантовой гравитации.
Сабина Хоссенфельдер предложила рассматривать двух альтернативных претендентов на «теорию всего» — теорию струн и петлевую квантовую гравитацию как стороны одной медали. Чтобы петлевая квантовая гравитация не противоречила специальной теории относительности, в ней необходимо ввести взаимодействия, которые похожи на рассматриваемые в теории струн. .
Проблемы теории
В модифицированной версии своей статьи Бильсон-Томпсон признает, что нерешенными проблемами в его модели остаются
спектр масс частиц,
спины ,
смешивание Кабиббо ,
а также необходимость привязки его модели к более фундаментальным теориям.
В более позднем варианте статьи описывается динамика брэдов с помощью переходов Пачнера (англ.
Pachner moves).
См. также
Источники
- , «Элементы большой науки»
Напишите отзыв о статье «Петлевая квантовая гравитация»
Литература
- Lee Smolin,
Three Roads to Quantum Gravity, Basic Books, 2001. - John Baez,
The Quantum of Area?, Nature, vol.421, pp. 702–703; February 2003. - Lee Smolin, , arxiv.org/hep-th/0303185.
- Welcome to Quantum Gravity. Special Section, Physics World, Vol.16, No.11, pp. 27–50; November 2003.
-
Олег Фейгин.. — М
.: Эксмо, 2012. — 288 с. — (Тайны мироздания). — 3000 экз.
— ISBN 9785699530168 .
Примечания
| Теории гравитации | |||
| Стандартные теории гравитации | Альтернативные теории гравитации | Квантовые теории гравитации | Единые теории поля |
|---|---|---|---|
Классическая физика
Принципы
|
Классические
Релятивистские |
|
Многомерные
Струнные
Прочие |
Отрывок, характеризующий Петлевая квантовая гравитация
В Лысых Горах, имении князя Николая Андреевича Болконского, ожидали с каждым днем приезда молодого князя Андрея с княгиней; но ожидание не нарушало стройного порядка, по которому шла жизнь в доме старого князя. Генерал аншеф князь Николай Андреевич, по прозванию в обществе le roi de Prusse, [король прусский,] с того времени, как при Павле был сослан в деревню, жил безвыездно в своих Лысых Горах с дочерью, княжною Марьей, и при ней компаньонкой, m lle Bourienne. [мадмуазель Бурьен.] И в новое царствование, хотя ему и был разрешен въезд в столицы, он также продолжал безвыездно жить в деревне, говоря, что ежели кому его нужно, то тот и от Москвы полтораста верст доедет до Лысых Гор, а что ему никого и ничего не нужно. Он говорил, что есть только два источника людских пороков: праздность и суеверие, и что есть только две добродетели: деятельность и ум. Он сам занимался воспитанием своей дочери и, чтобы развивать в ней обе главные добродетели, до двадцати лет давал ей уроки алгебры и геометрии и распределял всю ее жизнь в беспрерывных занятиях. Сам он постоянно был занят то писанием своих мемуаров, то выкладками из высшей математики, то точением табакерок на станке, то работой в саду и наблюдением над постройками, которые не прекращались в его имении. Так как главное условие для деятельности есть порядок, то и порядок в его образе жизни был доведен до последней степени точности. Его выходы к столу совершались при одних и тех же неизменных условиях, и не только в один и тот же час, но и минуту. С людьми, окружавшими его, от дочери до слуг, князь был резок и неизменно требователен, и потому, не быв жестоким, он возбуждал к себе страх и почтительность, каких не легко мог бы добиться самый жестокий человек. Несмотря на то, что он был в отставке и не имел теперь никакого значения в государственных делах, каждый начальник той губернии, где было имение князя, считал своим долгом являться к нему и точно так же, как архитектор, садовник или княжна Марья, дожидался назначенного часа выхода князя в высокой официантской. И каждый в этой официантской испытывал то же чувство почтительности и даже страха, в то время как отворялась громадно высокая дверь кабинета и показывалась в напудренном парике невысокая фигурка старика, с маленькими сухими ручками и серыми висячими бровями, иногда, как он насупливался, застилавшими блеск умных и точно молодых блестящих глаз.
В день приезда молодых, утром, по обыкновению, княжна Марья в урочный час входила для утреннего приветствия в официантскую и со страхом крестилась и читала внутренно молитву. Каждый день она входила и каждый день молилась о том, чтобы это ежедневное свидание сошло благополучно.
Сидевший в официантской пудреный старик слуга тихим движением встал и шопотом доложил: «Пожалуйте».
Из за двери слышались равномерные звуки станка. Княжна робко потянула за легко и плавно отворяющуюся дверь и остановилась у входа. Князь работал за станком и, оглянувшись, продолжал свое дело.
Огромный кабинет был наполнен вещами, очевидно, беспрестанно употребляемыми. Большой стол, на котором лежали книги и планы, высокие стеклянные шкафы библиотеки с ключами в дверцах, высокий стол для писания в стоячем положении, на котором лежала открытая тетрадь, токарный станок, с разложенными инструментами и с рассыпанными кругом стружками, – всё выказывало постоянную, разнообразную и порядочную деятельность. По движениям небольшой ноги, обутой в татарский, шитый серебром, сапожок, по твердому налеганию жилистой, сухощавой руки видна была в князе еще упорная и много выдерживающая сила свежей старости. Сделав несколько кругов, он снял ногу с педали станка, обтер стамеску, кинул ее в кожаный карман, приделанный к станку, и, подойдя к столу, подозвал дочь. Он никогда не благословлял своих детей и только, подставив ей щетинистую, еще небритую нынче щеку, сказал, строго и вместе с тем внимательно нежно оглядев ее:
– Здорова?… ну, так садись!
Он взял тетрадь геометрии, писанную его рукой, и подвинул ногой свое кресло.
– На завтра! – сказал он, быстро отыскивая страницу и от параграфа до другого отмечая жестким ногтем.
Княжна пригнулась к столу над тетрадью.
– Постой, письмо тебе, – вдруг сказал старик, доставая из приделанного над столом кармана конверт, надписанный женскою рукой, и кидая его на стол.
Лицо княжны покрылось красными пятнами при виде письма. Она торопливо взяла его и пригнулась к нему.
– От Элоизы? – спросил князь, холодною улыбкой выказывая еще крепкие и желтоватые зубы.
– Да, от Жюли, – сказала княжна, робко взглядывая и робко улыбаясь.
– Еще два письма пропущу, а третье прочту, – строго сказал князь, – боюсь, много вздору пишете. Третье прочту.
– Прочтите хоть это, mon pere, [батюшка,] – отвечала княжна, краснея еще более и подавая ему письмо.
– Третье, я сказал, третье, – коротко крикнул князь, отталкивая письмо, и, облокотившись на стол, пододвинул тетрадь с чертежами геометрии.
– Ну, сударыня, – начал старик, пригнувшись близко к дочери над тетрадью и положив одну руку на спинку кресла, на котором сидела княжна, так что княжна чувствовала себя со всех сторон окруженною тем табачным и старчески едким запахом отца, который она так давно знала. – Ну, сударыня, треугольники эти подобны; изволишь видеть, угол abc…
Княжна испуганно взглядывала на близко от нее блестящие глаза отца; красные пятна переливались по ее лицу, и видно было, что она ничего не понимает и так боится, что страх помешает ей понять все дальнейшие толкования отца, как бы ясны они ни были. Виноват ли был учитель или виновата была ученица, но каждый день повторялось одно и то же: у княжны мутилось в глазах, она ничего не видела, не слышала, только чувствовала близко подле себя сухое лицо строгого отца, чувствовала его дыхание и запах и только думала о том, как бы ей уйти поскорее из кабинета и у себя на просторе понять задачу.
Старик выходил из себя: с грохотом отодвигал и придвигал кресло, на котором сам сидел, делал усилия над собой, чтобы не разгорячиться, и почти всякий раз горячился, бранился, а иногда швырял тетрадью.
Княжна ошиблась ответом.
– Ну, как же не дура! – крикнул князь, оттолкнув тетрадь и быстро отвернувшись, но тотчас же встал, прошелся, дотронулся руками до волос княжны и снова сел.
Он придвинулся и продолжал толкование.
– Нельзя, княжна, нельзя, – сказал он, когда княжна, взяв и закрыв тетрадь с заданными уроками, уже готовилась уходить, – математика великое дело, моя сударыня. А чтобы ты была похожа на наших глупых барынь, я не хочу. Стерпится слюбится. – Он потрепал ее рукой по щеке. – Дурь из головы выскочит.
Она хотела выйти, он остановил ее жестом и достал с высокого стола новую неразрезанную книгу.
– Вот еще какой то Ключ таинства тебе твоя Элоиза посылает. Религиозная. А я ни в чью веру не вмешиваюсь… Просмотрел. Возьми. Ну, ступай, ступай!
Он потрепал ее по плечу и сам запер за нею дверь.
Княжна Марья возвратилась в свою комнату с грустным, испуганным выражением, которое редко покидало ее и делало ее некрасивое, болезненное лицо еще более некрасивым, села за свой письменный стол, уставленный миниатюрными портретами и заваленный тетрадями и книгами. Княжна была столь же беспорядочная, как отец ее порядочен. Она положила тетрадь геометрии и нетерпеливо распечатала письмо. Письмо было от ближайшего с детства друга княжны; друг этот была та самая Жюли Карагина, которая была на именинах у Ростовых:
Жюли писала:
«Chere et excellente amie, quelle chose terrible et effrayante que l»absence! J»ai beau me dire que la moitie de mon existence et de mon bonheur est en vous, que malgre la distance qui nous separe, nos coeurs sont unis par des liens indissolubles; le mien se revolte contre la destinee, et je ne puis, malgre les plaisirs et les distractions qui m»entourent, vaincre une certaine tristesse cachee que je ressens au fond du coeur depuis notre separation. Pourquoi ne sommes nous pas reunies, comme cet ete dans votre grand cabinet sur le canape bleu, le canape a confidences? Pourquoi ne puis je, comme il y a trois mois, puiser de nouvelles forces morales dans votre regard si doux, si calme et si penetrant, regard que j»aimais tant et que je crois voir devant moi, quand je vous ecris».
[Милый и бесценный друг, какая страшная и ужасная вещь разлука! Сколько ни твержу себе, что половина моего существования и моего счастия в вас, что, несмотря на расстояние, которое нас разлучает, сердца наши соединены неразрывными узами, мое сердце возмущается против судьбы, и, несмотря на удовольствия и рассеяния, которые меня окружают, я не могу подавить некоторую скрытую грусть, которую испытываю в глубине сердца со времени нашей разлуки. Отчего мы не вместе, как в прошлое лето, в вашем большом кабинете, на голубом диване, на диване «признаний»? Отчего я не могу, как три месяца тому назад, почерпать новые нравственные силы в вашем взгляде, кротком, спокойном и проницательном, который я так любила и который я вижу перед собой в ту минуту, как пишу вам?]
Прочтя до этого места, княжна Марья вздохнула и оглянулась в трюмо, которое стояло направо от нее. Зеркало отразило некрасивое слабое тело и худое лицо. Глаза, всегда грустные, теперь особенно безнадежно смотрели на себя в зеркало. «Она мне льстит», подумала княжна, отвернулась и продолжала читать. Жюли, однако, не льстила своему другу: действительно, и глаза княжны, большие, глубокие и лучистые (как будто лучи теплого света иногда снопами выходили из них), были так хороши, что очень часто, несмотря на некрасивость всего лица, глаза эти делались привлекательнее красоты. Но княжна никогда не видала хорошего выражения своих глаз, того выражения, которое они принимали в те минуты, когда она не думала о себе. Как и у всех людей, лицо ее принимало натянуто неестественное, дурное выражение, как скоро она смотрелась в зеркало. Она продолжала читать: 211
Написать заметку о петлевой квантовой гравитации меня побудили несколько вещей. И одна из них — на эту тему, из которого человек «не в теме» едва ли поймет вообще, о чем идет речь. Это просто гениально и совершенно для википедии бесполезно:
В своей статье 2005 года, С. Бильсон-Томпсон (Sundance Bilson-Thompson) предложил модель (по-видимому основанную на более общей теории брэдов (математических кос) М. Хованова (M. Khovanov)), в которой ришоны Харари (Harari) были преобразованы в протяжённые лентообразные объекты, называемые риббонами. Потенциально это могло бы объяснить причины самоорганизации субкомпонентов элементарных частиц, приводящие к возникновению цветового заряда, в то время как в предыдущей преонной (ришонной) модели базовыми элементами являлись точечные частицы, а цветовой заряд постулировался. Бильсон-Томпсон называет свои протяжённые риббоны «гелонами», а модель — гелонной. Данная модель приводит к интерпретации электрического заряда как топологической сущности, возникающей при перекручивании риббонов.
Ни фига тут нормальному человеку непонятно, а дело вот в чем.
Первая известная теория гравитации была создана еще Аристотелем. Он считал, что тела падают с разной скоростью, прямо пропорционально массе и обратно — плотности среды. Это почти правда при наличии трения. Впрочем, большого практического смысла в то время теория все равно не имела.
Научная же теория гравитации была создана Ньютоном, все ее проходили в школе, поэтому напоминать не буду. Ньютон описал закон, по которому тела притягиваются друг к другу. Но к 20му веку физики от выведения законов переключились на поиск причин. Стал важен вопрос не «как», а «почему». И никто иной как Энштейн предложил теорию гравитации, основанную на геометрии Римана: гравитация определяется кривизной четырехмерного пространства-времени. Физика оказалась промоделирована довольно абстрактной геометрией. Теория элегантна, и подтверждается экспериментально.
Однако, на этом физики не остановились. Дело в том, что в 20-30 годы была разработана квантовая механика, которая довольно быстро развилась в квантовую теорию поля. Суть в том, что физические величины перестали быть непрерывными, но принимающими ступенчатые, дискретные значения. Например, энергия. В квантовой теории поля «переносчиками» фундаментальных взаимодействий стали кванты, некоторые неделимые «кусочки». Самое простое — фотоны в электродинамике (или фотоны света, например). Или глюоны — в сильном взаимодействии кварков. Но суть похожа. Причем теории были выстроены таким образом, что на микро-уровне можно было «работать» на уровне квантов, но при непрерывном переходе к макро-уровню получались все типичные свойства поля. В физике известны 4 типа фундаментальных полей (взаимодействий), и три из них квантуются. Но не гравитация. Причем проблемы квантования гравитационного поля оказались настолько фундаментальными, что физики стали искать другие способы «связать» воедино все фундаментальные поля (зачем? чтобы объяснить, как устроен мир), и появились теории струн и другие Теории Всего, основанные на экзотических пространствах и симметриях.
У всех этих теорий было одно свойство, очень любимое математиками — геометрия пространства считалось непрерывной и гладкой. Собственно, так оно и есть в Римановой геометрии, использованной Энштейном. В середине 80х Ли Смолин с коллегами рискнули отказаться от гладкости и непрерывности, и им впервые удалось построить непротиворечивую квантовую модель гравитации при условии, что пространство тоже квантуемо! То есть состоит из «ячеек» планковской длины (десять в минус 33 см.), причудливым образом между собой соединенных. Для удобства представления, вместо ячеек они стали рассматривать узлы, а их соединения образуют то, что стали называть
спиновой сетью. Это позволяет задать любую, сколь угодно искривленную, геометрию. Неожиданно, вроде бы абстрактная математическая дисциплина — топология — вдруг стала востребована именно тут, так как именно она изучает подобного рода объекты.
Но спиновая сеть — это лишь мгновенный «снимок» состояния. В реальности, каждый момент времени в мире что-то происходит, и это выражается в трансформации сети. Сеть плюс время называется
спиновой пеной, потому что во времени сеть постоянно «бурлит», переживая бесконечные трансформации. Время «получилось» тоже дискретным, с интервалом между «тиками» десять в минус 43 см.
Как любая хорошая теория (и этим, кстати, она отличается от Теории Струн), квантовая теория гравитации допускает эксперименты, которые могут ее подтвердить или опровергнуть. На сегодняшний момент, современная аппаратура не позволяет поставить такие эксперименты — слишком малы эффекты, которые дает «зернистость» пространства — но техника и фантазия ученых не стоят на месте. Во всяком случае такие эксперименты не кажутся невозможными.
Также в последнее время доказано, что в петлевая квантовая гравитация «в пределе» приводит к энштейновской модели (впрочем, иначе она бы не имела смысла). Интересно, что в отличие от энштейновской теории, в «нашей» теории Вселенная существует и до Большого Взрыва.
Теперь настало время вернуться к тому, о чем же пишет Википедия. На самом деле, о важном. О том, что теория петлевой квантовой гравитации позволяет вывести
Возможно, будет полезно почитать:
- Дистанционное обучение на бухгалтерских курсах
; - Измерение величин Измеряется s в физике
; - Магнитные материалы и точка кюри
; - Квантовая теория гравитации
; - Аллегорический смысл оды «фелица»
; - Клеточная теория Основные постулаты клеточной
; - Тригонометрические уравнения — формулы, решения, примеры
; - Народы населяющие африку Какие народы населяли африканский континент история
;
Частые вопросы
Что такое квантовая гравитация простыми словами?
Ква́нтовая гравита́ция — направление исследований в теоретической физике, целью которого является квантовое описание гравитационного взаимодействия (и, в случае успеха, — объединение гравитации с остальными тремя фундаментальными взаимодействиями, описываемыми Стандартной моделью, то есть построение так называемой « …
Какие есть квантовые теории?
В основе квантовой теории поля лежат классическая теория поля, квантовая механика и специальная теория относительности (СТО).
Кто выдвинул теорию о квантах?
В октябре 1900 года немецкий физик Макс Планк ввел понятие кванта, которое противоречит классической физике. В отличие от многих других научных направлений, квантовая теория имеет точную дату своего рождения.
Кто открыл квантовое поле?
Лауреат Нобелевской премии по химии 1908 года. Нильс Бор (7 октября 1885, Копенгаген — 18 ноября 1962, Копенгаген) — датский физик-теоретик и общественный деятель, один из создателей современной физики. Известен как создатель первой квантовой теории атома и активный участник разработки основ квантовой механики.
Полезные советы
СОВЕТ №1
Перед тем как приступить к чтению статьи о петлевой квантовой теории гравитации, рекомендуется ознакомиться с основами общей теории относительности и квантовой механики, так как эти знания помогут лучше понять контекст и особенности новой теории.
СОВЕТ №2
При чтении статьи обратите внимание на историю развития квантовой теории гравитации, а также на основные принципы и постулаты, на которых она основана. Это поможет лучше понять суть и значение данной теории в современной физике.