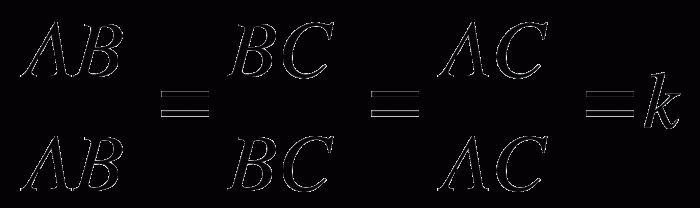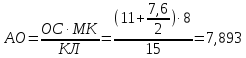Название проекта
Мнение эксперта:
Проектно-исследовательская работа, посвященная подобию треугольников в реальной жизни и измерению высоты методом Жюля Верна, представляет собой важное направление в научной деятельности. Эксперты отмечают, что данная тема имеет широкие практические применения в различных областях, включая геодезию, строительство, архитектуру и геологию. Исследования в этой области способствуют развитию новых методов и технологий, что в свою очередь оказывает положительное влияние на различные отрасли промышленности и научные открытия. Таким образом, проектно-исследовательская работа по изучению подобия треугольников и методам измерения высоты является актуальной и перспективной сферой научных исследований.

Краткая аннотация проекта
Проект подготовлен с применением проектной технологии. Реализуется в рамках программы по геометрии 8 класса по теме «Признаки подобия треугольников». Проект включает в себя информационную и исследовательскую часть. Аналитическая работа с информацией систематизирует знания о подобных фигурах. Самостоятельные исследования учащихся, а также приобретённые
практические знания
, умения и навыки учат видеть важность данного теоретического материала при применении его на практике. Дидактические задания помогут проконтролировать степень усвоения учебного материала.
Интересные факты
- Метод Жюля Верна для измерения высоты объекта. Этот метод основан на принципе подобия треугольников. Для измерения высоты объекта необходимо найти два треугольника, один из которых подобен треугольнику, образованному объектом и его тенью. Затем можно использовать пропорции между сторонами подобных треугольников, чтобы найти высоту объекта. Этот метод был описан Жюлем Верном в его романе «Пять недель на воздушном шаре».
- Использование подобия треугольников в архитектуре. Подобие треугольников используется в архитектуре для создания симметричных и пропорциональных зданий. Например, в греческом храме Парфенон фронтоны (треугольные элементы над колоннами) подобны друг другу. Это создает ощущение гармонии и равновесия.
- Использование подобия треугольников в картографии. Подобие треугольников используется в картографии для создания карт. Карты являются уменьшенными копиями реального мира, и для того, чтобы они были точными, необходимо использовать принцип подобия треугольников. Это означает, что углы и пропорции между сторонами треугольников на карте должны быть такими же, как в реальном мире.

Направляющие вопросы
Основополагающий вопрос: «Говорит ли природа языком подобия?»
«А можно ли найти примеры подобия вокруг нас?», «Как же мне измерить высоту своего дома?», «Зачем нужны подобные треугольники?»
Опыт других людей
Проектно-исследовательская работа, посвященная подобию треугольников в реальной жизни и методу измерения высоты по Жюлю Верну, вызвала живой интерес у многих людей. Участники проекта отмечают, что изучение подобия треугольников помогает им лучше понять окружающий мир и применять математические знания на практике. Метод измерения высоты по Жюлю Верну также вызвал интерес и обсуждения. Люди высказывают мнение, что данная тема имеет большое практическое значение и может быть полезной в различных областях, от строительства до геодезии.

План проекта
1.Мозговой штурм (формирование тем исследований учащихся).
2.Формирование групп для проведения исследований, выдвижение гипотез, обсуждение путей решения проблем.
3.Выбор творческого названия проекта.
4.Обсуждение плана теоретической и практической работы учащихся в группе.
5.Обсуждение с учащимися возможных источников информации.
6.Самостоятельная работа групп.
7.Подготовка учащимися презентаций и докладов по отчёту о проделанной работе.
8.Представление исследовательских работ.
XXV
юбилейный городской конкурс учебно-исследовательских
работ учащихся
Управление образования администрации г. Кунгура
Научное общество учащихся
секция
Геометрия
Кустова Екатерина МАОУ СОШ № 13
8«а» класс
Руководитель:
Гладких Татьяна Григорьевна
МАОУ СОШ №13
учитель математики
высшей категории
Кунгур,2017
ОГЛАВЛЕНИЕ
Введение……………………………………………………………………………3
Глава 1.
Бесподобное подобие
1.1. Из истории подобия ………………………………………………………….5
1.2. Понятие подобия ……………………………………………………………..6
1.3.Способы измерения предметов с применением подобия
1.3.1. Первый способ измерения высоты предмета………………………….8
1.3.2. Второй способ измерения высоты предмета………………………….9
1.3.3. Третий способ измерения высоты предмета…………………………..11
2.1. Измерение высоты объекта…………………………………………………..12
2.1.1. По длине тени………………………………….. ………………………12
2.1. 2. С помощью шеста………………………………………………………13
2.1.3. С помощью зеркала………………………………………………………13
2.1.4. Как поступил сержант……………………………………………………14
2.1.5. Не приближаясь к дереву ……………………………………………….16
2.2.Очистка пруда. ………………………………………………………………………17
2.2.1. Способы очистки водоемов……………………………………………..17
2.2.2. Измерение ширины пруда………………………………………………18
Заключение …………………………………………………………………… … ..22
Список литературы …………………………………………………………………23
Подобие красоты
Порой не замечаем мы,
Мы говорим « Подобен Божеству»,
Подразумевая идеал.
ВВЕДЕНИЕ
Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, полученные из наблюдений и опытов. Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз древней школы был: «Не знающие геометрии не допускаются!»
В наше время геометрические знания по-прежнему находят широкое применение в строительстве, архитектуре, искусстве, а также во многих отраслях промышленности. На уроках геометрии мы изучили тему «Подобие треугольников», и меня заинтересовал вопрос, как данную тему можно применить на практике.
Вспомните произведение Л. Керолла «Алиса в стране чудес». Какие изменения происходили с
главной героиней
: то она вырастала до нескольких футов, то уменьшалась до нескольких дюймов, всегда оставаясь, впрочем, сама собой. О каком преобразовании с точки зрения геометрии идет речь? Конечно, о преобразовании подобия.
Цель работы:
Нахождение области применения подобия треугольников в жизни человека.
Задачи:
1.Изучить
научную литературу
по данной теме.
2.Показать применение подобия треугольников на примере измерительных работ.
Гипотеза.С помощью подобия треугольников можно выполнять измерения реальных объектов.
Методы исследования:поиск, анализ, математическое моделирование.
Глава1.Бесподобное подобие
1.1.Из истории подобия
В основе подобия фигур лежит принцип отношения и пропорции. Идея отношения и пропорции зародилась в глубокой древности. Об этом свидетельствуют древнеегипетские храмы, детали гробницы Менеса и знаменитых пирамид в Гизе (III тысячелетие до н. э.), вавилонские зиккураты (ступенчатые культовые башни), персидские дворцы и другие памятники древности. Многие обстоятельства, в том числе особенности архитектуры, требования удобства, эстетики, техники и экономичности при возведении зданий и сооружений, вызвали возникновение и развитие понятий отношения и пропорциональности отрезков, площадей и других величин. В «Московском» папирусе при рассмотрении отношения большего катета к меньшему в одной из задач на прямоугольный треугольник применяется специальный знак для понятия «отношение». В «Началах» Евклида учение об отношениях излагается дважды. В VII книге содержится арифметическая теория. Она относится только к соизмеримым величинам и к целым числам. Эта теория создана на основе практики действия с дробями. Евклид применяет ее для исследования свойств целых чисел. В V книге излагается
общая теория
отношений и пропорций, разработанная Евдоксом. Она лежит в основе учения о подобии фигур, изложенного в VI книге «Начал», где находится определение: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».
Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров.
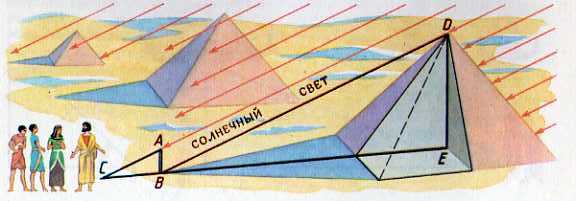
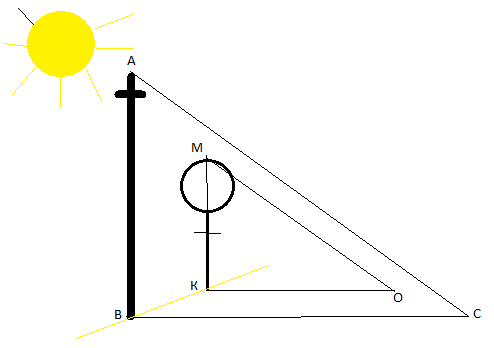
Пропорциональность отрезков, образующихся на прямых, пересеченных несколькими параллельными прямыми, была известна еще вавилонским ученым. Хотя некоторые приписывают это открытие Фалесу Милетскому. Древнегреческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Жрецы и фараон, собравшиеся у подножия пирамиды, озадаченно смотрели на северного пришельца, отгадывавшего по тени высоту огромного сооружения. Фалес, — говорит предание, — избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна также равняться длине отбрасываемой ею тени.
До наших дней сохранилась клинописная табличка, в которой
речь идет
о построении пропорциональных отрезков путем проведения в прямоугольном треугольнике параллелей к одному из катетов.
1.2.Понятие подобия.
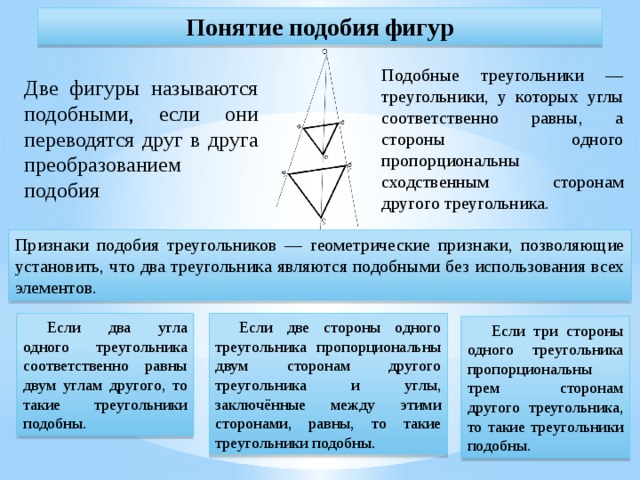
В жизни мы встречаемся не только с равными фигурами, но и с такими, которые имеют одинаковую форму, но разные размеры. Геометрия называет такие фигуры подобными.
У всех подобных фигур одинаковые формы, но разные размеры.
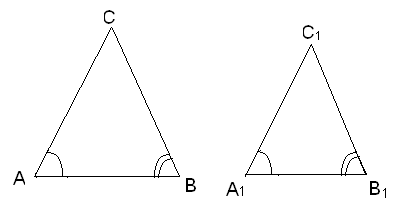
Определение:Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Если треугольник ABC подобен треугольнику А
1
B
1
С
1
, то углы А, В и С равны соответственно углам A
1
, B
1
и C
1
,
. Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Замечание 1:
Равные треугольники
подобны с коэффициентом 1.
Замечание 2: При обозначении подобных треугольников следует упорядочить их вершины таким образом, чтобы углы при них были попарно равны.
Замечание 3: Требования, которые перечислены в определении подобных треугольников, являются избыточными.
Свойства подобных треугольников
Отношение соответственных линейных элементов подобных треугольников равно коэффициенту их подобия. К таким элементам подобных треугольников относятся те, которые измеряются в единицах длины. Это, например, сторона треугольника, периметр, медиана. Угол или площадь к таким элементам не относятся.
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.
Признаки подобия треугольников.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
1.3.Способы измерения предметов с применением признаков подобия
1.3.1.
Первый способизмерения высоты предмета
В солнечный день не составляет труда измерение высоты предмета, предположим дерева, по его тени. Необходимо только, взять предмет (например, палку) известной длины и установить ее перпендикулярно поверхности. Тогда от предмета будет падать тень. Зная высоту палки, длину тени от палки, длину тени от предмета, высоту которого мы измеряем, можно определить высоту предмета. Для этого нудно рассмотреть подобие двух треугольников. Помните: солнечные лучи падают параллельно друг другу.
Притча
«Усталый чужеземец пришёл в страну Великого Хапи. Солнце уже садилось, когда он подошёл к великолепному дворцу фараона. Он что-то сказал слугам. По мгновению распахнули перед ним двери и провели его в приёмную залу. И вот он стоит в запылённом походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители великих тайн природы.
К
то ты? –спросил верховный жрец.
Зовут меня Фалес. Родом я из Милета.
Жрец надменно продолжал:
Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на неё? – Жрецы согнулись от хохота. – Будет хорошо, — насмешливо продолжал жрец, — если ты ошибёшься не более чем на 100 локтей.
Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.
Лица жрецов потемнели. Какая наглость! Этот чужеземец утверждает, что может вычислить то, чего не могут они – жрецы великого Египта.
Хорошо, — сказал фараон. – Около дворца стоит пирамида, мы знаем её высоту. Завтра проверим твоё искусство».
На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту. Что сказал Фалес?
Слова Фалеса
: Когда тень от палки стала той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины имеет ту же длину, что и сама пирамида.
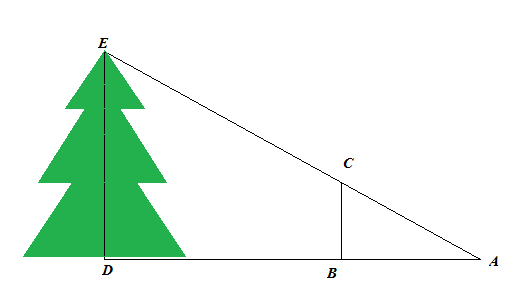
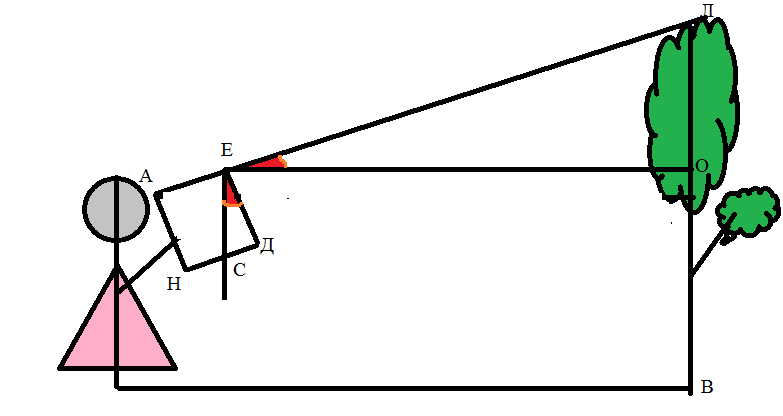
1.3.2.Второй способизмерения высоты предмета
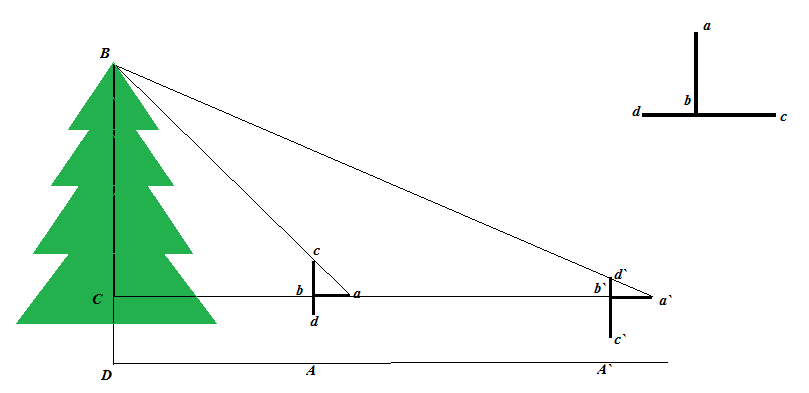
был предметно описан у Жюля Верна в романе «Таинственный Остров». Этот способ можно применять, когда нет солнца и не видно тени от предметов. Для измерения нужно взять шест, равный по длине вашему росту. Шест этот надо установить на таком расстоянии от предмета, чтобы лежа можно было видеть верхушку предмета на одной прямой линии с верхней точкой шеста. Тогда высоту предмета можно найти, зная длину линии, проведенной от вашей головы до основания предмета.
Отрывок из романа.
«-Сегодня нам надо измерить высоту площадки Дальней скалы, — сказал инженер.
Вам понадобится для этого инструмент? – спросил Герберт.
Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и
точному способу
. Юноша, стараясь научиться, возможно, большему, последовал за инженером, который спустился с гранитной стены до окраины берега.
Взяв прямой шест, длиной 12 футов, инженер измерил его возможно точнее, сравнивая со своим ростом, который был хорошо ему известен. Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком.Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 500 футам.
«-Тебе знакомы зачатки геометрии? – спросил он Герберта, поднимаясь с земли.
Помнишь свойства подобных треугольников
-Да.
-Их сходственные стороны пропорциональны.
-Правильно. Так вот: сейчас я построю 2 подобных прямоугольных треугольника. У меньшего одним катетом, будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же – мой луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же – мой луч зрения, совпадающий с направлением гипотенузы первого треугольника.
…Если мы измерим два расстояния: расстояние от колышка до основания шеста и расстояние от колышка до основания стены, то, зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, т. е. высоту стены. Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее – 500 футам. По окончании измерений инженер составил следующую запись:
15: 500 = 10: х; 500 х 10 = 5000; 5000: 15 = 333,3.
Значит, высота гранитной стены равнялась 333 футам.
1.3.3.Третий способ
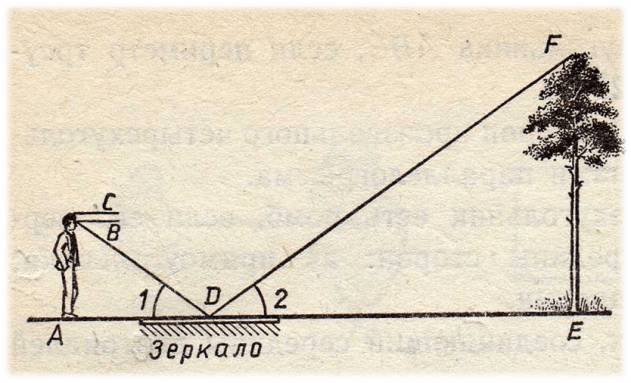
Определение высоты предмета по зеркалу.
Зеркало кладут горизонтально и отходят от него назад в такую точку, стоя в которой, наблюдатель видит в зеркале верхушку дерева. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до зеркала больше, чем расстояние от зеркала до вас. Помните: угол падения равен углу отражения (закон отражения).
АВ
D
подобен
EFD
(по двум углам)
:
ВА
D
=
FED
=90°;
А
D
В =
EDF
, т.к. угол падения равен углу отражения.
В подобных треугольниках сходственные стороны пропорциональны:
Глава 2. Использование подобия треугольников на практике
2. 1. Измерение высоты объекта
В качестве измеряемого объекта возьмём дерево.
2.1.1. По длине тени
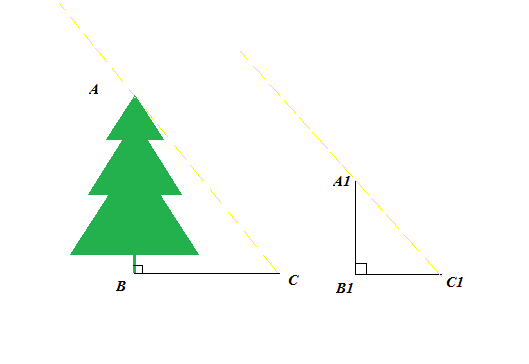
В основе этого метода лежит видоизмененный способ Фалеса, позволяющий использовать тень любой длины. Для измерения высоты дерева необходимо на некотором отдалении от дерева воткнуть в землю шест.
AB
– высота дерева
BC
– длина тени дерева
A 1
B
1
– высота шеста
B 1
C
1
– длина тени шеста
B =
Треугольник АВС подобен треугольнику А
1
В
1
С
1
.
Выполнив необходимые измерения, мы можем найти высоту дерева.
АВ=
ВС.
А
1
В
1
В
1
С
1
АВ =
А
1
В
1
∙ ВС.
В
1
С
1
2.1.2 С помощью шеста
Шест длиной приблизительно равный росту человека втыкается в землю отвесно. Место для шеста надо выбрать так, чтобы человек, лежащий на земле, видел верхушку дерева на одной прямой с верхней точкой шеста.
ADE т. к.
AD=
ED, ED =
AD ∙ BC.
AB
BC
AB
О
A
B
C
A
1
C
1
пределение высоты по тени.
A
1
B
1
=1,6 м
А
1
С
1
=2,8 м
АС=17 м
2.1.3. С помощью зеркала.
На некотором расстоянии от дерева на ровной земле кладётся зеркало, и отходят от него назад в такую точку, стоя в которой наблюдатель видит верхушку дерева.
АВ – высота дерева
АС – расстояние от дерева до зеркала
CD
– расстояние от человека до зеркала
ED
– рост человека.
Треугольник АВС подобен треугольнику
DEC
т. к.
AC=
AB,
DC ED
AB =
AC ∙ ED.
О
пределение высоты предмета с помощью зеркала.
AB=1,5
м
DE=12,5
м
AD= 2,7
м
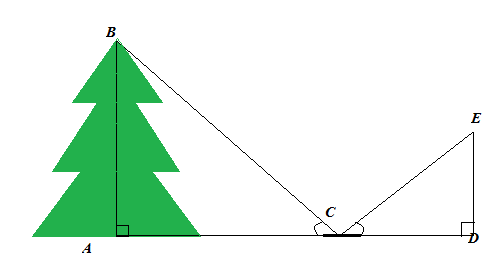
2.1.4. Как поступил сержант.
Некоторые из только что описанных способов измерения высоты неудобны тем, что вызывают необходимость ложиться на землю. Можно, разумеется, избежать такого неудобства.
Вот как однажды было на одном из фронтов Великой
Отечественной войны
. Подразделению лейтенанта Иванюк было приказано построить мост через горную реку. На противоположном берегу засели фашисты. Для разведки места постройки моста лейтенант выделил разведывательную группу во главе со старшим сержантом. В ближайшем
лесном массиве
они измерили диаметр и высоту наиболее типичных деревьев, которые можно было использовать для постройки.
Высоту деревьев определяли при помощи шеста так, как показано на рис.
Этот способ состоит в следующем.
Запасшись шестом выше своего роста, воткните его в землю отвесно на некотором расстоянии от измеряемого дерева. Отойдите от шеста назад, по продолжению
Dd
до того места
A
, с которого, глядя на вершину дерева, вы увидите на одной линии с ней верхнюю точку
b
шеста. Затем, не меня положения головы, смотрите по направлению горизонтальной прямой аС, замечая точки с и С, в которых луч зрения встречает шест и ствол. Попросите помощника сделать в этих местах пометки, и наблюдение окончено.
треугольник
abc
подобен треугольнику
aBC
=>
BC=
aC, BC = bc ∙
aC.
Bc
ac
ac
Расстояние
bc
,
aC
и ас легко измерить непосредственно. К полученной величине ВС нужно прибавить расстояние
CD
(которое также измеряется непосредственно), чтобы узнать искомую высоту дерева.
2.1.5.
Не приближаясь к дереву.
Случается, что почему – либо неудобно подойти вплотную к основанию измеряемого дерева. Можно ли в таком случае определить его высоту?
Вполне возможно. Для этого придуман остроумный прибор, который легко изготовить самому. Две планки
ad
и с
d
скрепляют под прямым углом так, чтобы
ab
равнялось
bc
, а
bd
составляло половину
ad
. Вот и весь прибор. Чтобы измерить им высоту, держат его в руках, напротив планку
cd
вертикально (для чего при ней имеется отвес – шнурок с грузиком), и становится последовательно в двух местах: сначала в точке А, где располагают прибор концом с вверх, а затем в точке А`, подальше, где прибор держат вверх концом
d
. Точка А избирается так, чтобы, глядя из а на конец с, видеть его на одной прямой с верхушкой дерева. Точку
же А` отыскивают так, чтобы, глядя из а` на точку
d
`, видеть её совпадающей с В.
Треугольник ВСа подобен треугольнику
bca
т. к.
Треугольник ВСа` подобен треугольнику
b
`
d
`
a
` т. к.
В отыскивании двух точек А и А` заключается все измерение, потому что искомая часть ВС равна расстоянию АА`. Равенство вытекает из того, что аС = ВС, так как треугольник
abc
равнобедренний (по построению). Следовательно и треугольник
aBC
равнобедренный. а`
C
= 2
BC
вытекает из соотношений в подобных треугольниках; значит,
a
`
C
–
aC
=
BC
.
О
пределение высоты с помощью прямоугольного равнобедренного треугольника.
CD
=
AB
+
BD
AB
= 8,9 м
BD
=1,2 м
С
D
=8,9+1,2≈10 м
2.2.Очистка пруда.
На поселке Кирова есть пруд, который очень загрязнен. Мы решили выяснить, какими способами можно его очистить.
2.2.1.Способы очистки водоемов.
Очистка водоемов производится механизированным, гидромеханизированным, взрывным и ручным способами. Самый распространенный из всех способов- механический. При этом способе применяется чистка земснарядом.
Земснаряд НСС – 400/20 – ГР
Производительность (намыв грунта): 800м/куб за смену. Размеры: длина 10 м. , ширина 2, 7 м, высота 3, 0 м.
Вес: 17 тонн. Пульпопровод: 100м (в том числе – 50 м плавучий, 50 м – береговой). Земснаряд оборудован стрелой. Длина стрелы — 10 м, с гидроразмывом (подача 60 м/куб в час воды при напоре 40 м, мощность насоса 7 кВт).
Двигатель: Д-260-4. 01 (210 л/с, расход топлива — 14 л/час, частота вращения — 1800 об/мин). Насос: ГРАУ 400/20.
Технические характеристики
насоса: выход грунта 10-30% в час, напор водяного столба — 20м, мах мощность — 75 кВт, частота вращения — 950 об/мин. Земснаряд данной модификации поднимает грунт с глубины водоема 1-9, 5 м. , проталкивание по пульпопроводу до 200м. Диаметр трубопровода: 160 мм. Энергообеспечение: автономное. Движение при помощи лебёдок — 4 двигателя по 1, 5 кВт
.
В нашем конкретном случае нас интересует длина стрелы земснаряда – 10м.
2.2.2.Измерение ширины пруда.
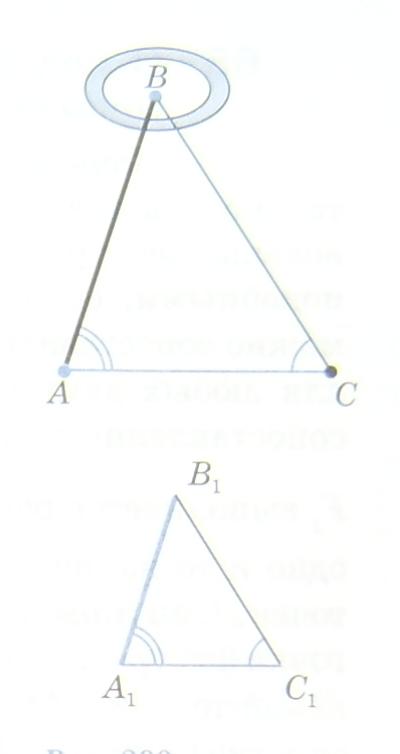
Свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности. Мы рассмотрим одну задачу: определение расстояния до недоступной точки. Для примера мы попробуем измерить ширину пруда с помощью признаков подобия треугольников.
Итак, с помощью некоторых приборов и расчетов, приступаем к работе. Для получения более точных результатов, мы измерили пруд в двух местах.
Предположим, что нам нужно найти расстояние от точки А на берегу, на котором стоим мы, до точки
B
, находящейся на противоположном берегу реки. Для этого выбираем точку С на «нашем» берегу, попутно измерив получившийся отрезок АС. Затем с помощью астролябии измеряем углы А и С. На листе бумаги строим треугольник
A
1
B
1
C
1
, так, чтобы соблюдался 1 признак подобия треугольников (по 2 углам). Угол
A
1
равен углу А, а угол
C
1
равен углу
C
. Измеряем стороны
A
1
B
1
и
A
1
C
1
треугольника
A
1
B
1
C
1
.Так как треугольники
ABC
и
A
1
B
1
C
1
подобны, то
AB
/
A
1
B
1
=
AC
/
A
1
C
1
, откуда получаем
AB
=
AC
*
A
1
B
1
/
A
1
C
1
Эта формула позволяет по известным расстояниям
AC
,
A
1
C
1
и
A
1
B
1
найти расстояние
AB
.
Приборы:
Астролябия, линейка демонстрационная (или, к примеру, веревка длиной примерно 4 м).
Предварительные измерения:
Мы измерили пруд в двух местах, поэтому по очереди опишем каждое измерение.
1) Возьмем любую точку на противоположном берегу, находящуюся рядом с границей пруда и земли, скажем, небольшую ямку или, если предварительно подготовиться, вбитый в землю колышек, веха.
Получилось 88 градусов, первый угол у нас есть. Таким же образом, поставив прибор на точку С, находящуюся на расстоянии, в нашем случае, 4 метра от точки А, измеряем угол С. 70 градусов. И, собственно, на этом измерения закончились.
2) На втором месте, где мы измеряли ширину реки, у нас получились примерно равные с первым случаем углы: А=90, С=70 градусов.
Расчеты:
Чертим треугольник
A
1
B
1
C
1
, в котором угол
A
1
=88 , а угол
C
1
=70 градусов. Отрезок
A
1
C
1
, для простоты измерений берем равный 4 сантиметра. Теперь измеряем отрезок
A
1
B
1
. Получилось примерно 11 см. Переводим результаты в метры и собираем их в пропорцию:
AB/
A
1
B
1
= AC/
A
1
C
1
AB-? ;
A
1
B
1
=0,11
м
; AC=4
м
;
A
1
C
1
=0,04
м
.
Выражаем
АВ
:
AB =AC*
A
1
B
1
/
A
1
C
1
;
АВ
=4*0,11/0,04;
АВ=0,44/0,04=11м
Итак, в первом случае ширина пруда равна 11 м.
Следуя тем же способом, находим все стороны и составляем пропорцию. Но результаты, так как углы примерно равны, получились такие же. Итак, мы измерили ширину пруда в двух местах и получили один результат – 11 метров.
Раннее я указывала, что длина стрелы земснаряда равна 10 метров, т.е. её вполне хватает для того, чтобы с одного берега очистить пруд.
Итак, мое предположение о том, что геометрия, а
данном случае
подобие треугольников, помогает решать социальные проблемы верно. Я доказала, что с помощью подобия можно рассчитать высоту зданий и ширину пруда.
Ведь иногда так хочется, чтобы твой родной уголок, место в котором мы с вами живем, засияло новыми красками, вызывало гордость. Хочется спуститься в любом месте на речку или пруд и искупаться, не опасаясь за свое здоровьё. Хочется гордиться своей малой Родиной. А для этого мы все должны постараться. Все в наших руках.
Я исследовала различные способы измерения высоты и ширины объектов на местности с помощью подобия треугольников
Заключение
Я узнала много нового о применении подобия треугольников.
Как найти расстояние до недоступной точки? Как путём построения подобных треугольников найти расстояние между двумя недоступными пунктами А и В? Как найти высоту предмета, к основанию которого можно подойти?
Решение подобных задач способствует развитию
логического мышления
, умению анализировать ситуацию, а использование метода подобия треугольников в их решении, повышает тем самым математическую культуру, развивая математические способности.
Использовать рассмотренный мною геометрический материал можно как на уроках геометрии и физики, так и при подготовке к Государственной итоговой аттестации,
Геометрия – это наука, которая обладает всеми свойствами хрустального стекла, такая же прозрачная в рассуждениях, безупречная в доказательствах, ясная в ответах, гармонично сочетающая в себе прозрачность мысли и красоту
человеческого разума
. Геометрия до конца не изученная наука, и может быть, многие открытия ждут именно вас.
Литература:
1. Глейзер Г.И. История математики в школе 7-8 кл. — М.: Просвещение, 1982.-240 с.
2. Савин А.П.Я познаю мир — М.: ООО «Издательство АСТ-ЛТД»,1998.-480 с.
3. Савин А.П.
Энциклопедический словарь
юного математика. — М.:Педагогика, 1989,-352 с.
4. Атанасян Л.С. и др. Геометрия7-9: Учеб. для общеобразоват. учреждений. — М.: Просвещение, 2005г,-245с.
5. Г.И Баврин. Большой справочник школьника. Математика. М. дрофа. 2006г. 435с
6.Я. И. Перельман. Занимательная геометрия. Домодедово. 1994г. 11-27с.
7.
http
://
canegor
.
urc
.
ac
.
ru
/
zg
/59825123.
html
Разделы:Математика
Класс:8
Возможность для приобщения школьников к
учебной деятельности творческого характера
предоставляют математические задачи, а также
метод проектов, призванный развивать
любознательность, ответственность, умение
работать с информацией, умение работать
коллективно — в группе и т.д.
Данный проект предлагается выполнить учащимся
8 класса. Проект разработан в рамках темы
“Подобные фигуры”, на которую отводится 19 часов
учебного времени. Учебный проект по данной теме с
большим интересом воспринимается учениками и
позволяет создать условия, при которых ученики, с
одной стороны могут самостоятельно осваивать
новые знания и способы действия, а с другой —
применять на практике ранее приобретенные
знания и умения. При этом основной упор делается
на
творческое развитие
личности.
Учащиеся выполняют работу в группах, в процессе
итогового обсуждения результаты каждой группы
становятся достоянием всех остальных.
Проект подготовлен во внеурочное время
учащимися 8 класса.
Проект включает в себя информационную и
исследовательскую часть.
На основе изучения источников учащиеся:
- познают возможность использования признаков
подобия треугольников в жизни; - систематизируют знания о подобных фигурах.
- расширяют свой кругозор знаний;
- изучают значение данной темы на уроках
геометрии.
Самостоятельные исследования учащихся, а также
приобретённые практические знания, умения и
навыки учат видеть важность данного
теоретического материала при применении его на
практике.
Дидактические задания помогут
проконтролировать степень усвоения учебного
материала.
Методическое представление
- Введение.
- Методический паспорт учебного проекта.
- Этапы реализации проекта
- Осуществление проекта.
- Выводы.
- Работы учащихся в рамках учебного проекта.
1. Введение
“Проект – это совокупность определенных
действий, документов, создание разного рода
теоретического продукта. Это всегда творческая
деятельность. В основе метода проектов лежит
развитие познавательных творческих навыков
учащихся; умений самостоятельно конструировать
свои знания, умений ориентироваться в
информационном пространстве, развитие
критического мышления”. (Е.С.Полат).
Педагог в этой ситуации не только активный
участник образовательного процесса: он не
столько учит, сколько понимает и чувствует, как
ребенок учится сам.
Учитель помогает ученикам в поиске источников;
сам является источником информации;
координирует весь процесс; поддерживает
непрерывную связь с детьми. Организует
представление результатов работы в различных
формах.
Анализируя учебный проект, педагог мысленно
представляет себе реакцию детей, обдумывает
форму предложения рассмотреть проблему, найти
решение задачи проекта, окунуться в ситуацию
сюжета.
Проект – это результат скоординированных
совместных действий группы или нескольких групп
учащихся.
2. Паспорт проекта
Название проекта
: Бесподобное подобие
Тема проекта: Подобные фигуры.
Вид проекта: учебный.
Типология проекта: практико-ориентированный,
индивидуально- групповой.
Предметные области: математика.
Гипотеза: Если человек знает признаки
подобия треугольников, возникнет ли
необходимость их применять в жизни?
Проблемные вопросы:
1. Где можно применить подобие треугольников в
измерении?
2. Почему для иллюстрации или объяснения
некоторых объектов или явлений люди делают
макеты?
3. Почему из маленького негатива получается
большая качественная фотография?
4. Как достичь то, что кажется недостижимым?
5. Почему в мире существует подобие?
7. Важно ли в жизни изучать признаки подобия
треугольников?
Цель проекта: углубить и расширить знания по
теме “Подобные фигуры”.
Методические задачи проекта:
- изучить признаки подобия треугольников;
- оценить важность темы “Подобие”
- развивать умение применять теоретический
материал при решении практических задач; - закрепить полученные
теоретические знания
на
практике; - развить интерес к науке и технике, через поиск
примеров применения данной темы в жизни; - расширить математический кругозор и изучить
новые подходы к решению задач; - приобрести навыки исследовательской работы.
Участники проекта: учащиеся 8 класса. Время
работы над проектом: февраль–март 2014 года.
Материально-техническое и учебно-методическое
оснащение: учебная и учебно-методическая
литература, дополнительная литература,
компьютер с доступом в Интернет.
3. Этапы реализации проекта
1 этап – погружение в проект (актуализация
знаний; формулировка тем; формирование групп)
(неделя);
2 этап – организация деятельности (сбор
информации; обсуждение в группе) (неделя);
3 этап – осуществление деятельности
(исследование; выводы (месяц);
4 этап – представление проектного продукта (2
недели).
4. Осуществление проекта
1-й этап: Погружение в проект (подготовительный
этап)
Выбрав темы своего исследования, учащиеся
разделились на группы, определили задачи и
спланировали свою деятельность.
Образовалось 5 проектных групп по 5 человек.
Были выбраны следующие темы будущих проектов:
1. Из истории подобия.
2. Подобие в задачах на ГИА.(Реальная математика)
Подобие в нашей жизни:
3. Определение высоты предмета.
4. Подобие в природе.
5. Поможет ли подобие треугольников людям
различных профессий?
Роль учителя – направляющая на основе
мотивации.
2-й этап: поисковый и исследовательский:
Учащиеся изучали дополнительную литературу,
собирали информацию по своей теме, распределили
обязанностей в каждой группе (в зависимости от
выбранной индивидуальной темы исследования);
делали нужные приборы для исследования,
проводили исследования, готовили наглядное
представление своих исследований.
Роль учителя – наблюдательная,
консультирующая, учащиеся в основном работали
самостоятельно.
3-й этап: результаты и выводы:
Учащиеся анализировали найденную информацию,
формулировали выводы. Оформляли результаты, шла
подготовка материалов для защиты проекта,
создания презентаций
4-й этап: презентация и защита проекта:
Проведение конференции, учащиеся публично,
наглядно представляют результат своей проектной
деятельности в виде мультимедийной презентации.
Роль учителя – сотрудничество.
5. Общие выводы. Заключение
Осуществление данного учебного проекта
позволило учащимся развить свои навыки работы не
только с
дополнительными источниками
по
математике, но и с компьютером, сформировать
навыки работы в сети Интернет, а также
коммуникативные способности учащихся.
Участие в осуществлении проекта позволило
углубить знания по применению математики в
различных областях, а также закрепить знания по
указанной теме. Следует отметить, что полученные
в ходе осуществления проекта знания извлекаются
с конкретной целью и являются объектом
заинтересованности ученика. Это способствует их
глубокому усвоению.
В целом работа по проекту прошла успешно, в ней
приняли участие практически все ученики 8 класса.
Каждый был вовлечен в мыслительную деятельность
по данной проблематике, приобрел новые знания
путем
самостоятельной работы
. На защите своего
проекта выступал каждый участник группы. На
заключительном этапе были апробированы
практические приемы работы, проведен самоанализ
в виде презентации.
Проектная деятельность учащихся способствует
истинному обучению, т.к. она:
- Личностно ориентирована.
- Характеризуется возрастанием интереса и
вовлеченности в работу по мере её выполнения. - Позволяет реализовать педагогические цели на
всех этапах. - Позволяет учиться на собственном опыте, на
реализации конкретного дела. - Приносит удовлетворение ученикам, видящим
продукт собственного труда.
Эти ценные моменты, которые дает участие в
проектах, необходимо шире использовать в
практике развития интеллектуальных и творческих
способностей школьников. Таким образом,
использование метода учебных проектов в
педагогической работе определяется
необходимостью формирования личности 21 века,
личности новой эпохи, когда определяющими
факторами развития общества будут интеллект
человека и информация.
Работа построениа на исследовании возможности применения подобия треугольников в реоальной жизни, выполнены эксперименты по измерению длины с помощью высотомера.
«11Сушко-t.doc»
ПОДОБИЕ ТРЕУГОЛЬНИКОВ В РЕАЛЬНОЙ ЖИЗНИ
Сушко Дарья Олеговна
Ученица 8 класса
КУ «ОШ
I
—
III
ступеней №11 г.Енакиево»
Икаева Марина Александровна
Учитель математики,
II
категория
КУ «ОШ
I
—
III
ступеней №11 г.Енакиево»
[email protected]
Геометрия зародилась в глубокой древности. Мир, в котором мы живем сегодня, также наполнен геометрией. Все предметы, окружающие нас, имеют геометрические формы. Это здания, улицы, растения, предметы обихода.
Актуальность моей темы заключается в том, что без каких — либо инструментов, только опираясь на подобие треугольников, можно измерить высоту столба, колокольни, дерева, ширину реки, озера, оврага, длину острова, глубину пруда и т.д.
Целью работы было найти области применения подобия треугольников в
реальной жизни
.
Задачами работы были
Объекты и предметы исследования
:высота: столб; дерево, модель пирамиды.
В ходе работы были применены следующие методы: обзор литературы,
практическая работа
, сравнение.
Работа носит практико-ориентированный характер, так как практическая значимость работы заключается в возможности использования результатов исследования на уроках геометрии, в
повседневной жизни
.
В результате выполнения работы были проведены измерения высоты столба, дерева, моделей, изготовленных автором.
Просмотр содержимого документа
Содержание:
Вступление
Понятие подобия фигур. Признаки подобия.
4.1 Определение высоты по тени
4.2. Измерение высоты методом Жюля Верна
4.3. Измерение высоты с помощью высотомера
5. Выводы
Вступление.
Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, полученные из наблюдений и опытов. Мир, в котором мы живем сегодня, также наполнен геометрией. Все предметы, окружающие нас, имеют геометрические формы. Это здания, улицы, растения, предметы обихода.
В повседневной жизни часто встречаются фигуры одинаковой формы, но разного размера. Такие фигуры в геометрии называют подобными. Моя работа посвящена подобию треугольников, так как, изучая эту тему на уроках математики, меня заинтересовало, как на практике применяются понятие подобия треугольников и признаки подобия.
Актуальность моей темы заключается в том, что без каких — либо инструментов, можно измерить высоту столба, колокольни, дерева, ширину реки, озера, оврага, длину острова, глубину пруда и т.д.
Задачами моей работы были
изучить литературу по данной теме;
изучить историю возникновения понятия подобия;
узнать, где применяется подобие треугольников;
измерить высоту столба при помощи подобия треугольников различными способами;
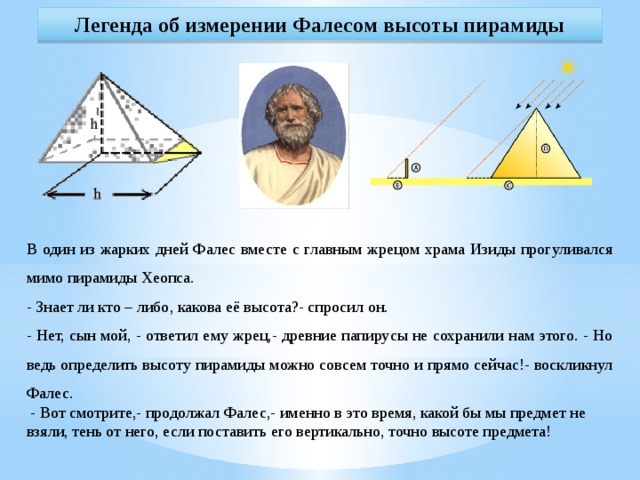
2. Легенда об измерении Фалесом высоты пирамиды.
С пирамидой связано много таинственных историй и легенд. В один из жарких дней Фалес вместе с главным жрецом храма Изиды прогуливался мимо пирамиды Хеопса.
Вот смотрите,- продолжал Фалес,- именно в это время, какой бы мы предмет не взяли, тень от него, если поставить его вертикально, точно высоте предмета! Чтобы воспользоваться тенью для решения задачи о высоте пирамиды, надо было знать уже некоторые геометрические свойства треугольника, — именно следующие два (из которых первое Фалес открыл сам):
1. Что углы при основании равнобедренного треугольника равны, и обратно – что стороны, лежащие против равных углов треугольника, равны между собою; 2. Что сумма углов всякого треугольника равна двум прямым углам.
Только вооружённый этим знанием Фалес вправе был заключить, что, когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и следовательно, вершина пирамиды, середина её основания и конец её тени должны обозначить равнобедренный треугольник. Этим
простым способом
очень удобно, казалось бы, пользоваться в ясный солнечный день для измерения одиноко стоящих деревьев, тень которых не сливается с тенью соседних. Но в наших широтах не так легко, как в Египте, подстеречь нужный для этого момент: Солнце у нас низко стоит над горизонтом, и тени бывают равны высоте отбрасывающих их предметов лишь в околополуденные часы летних месяцев. Поэтому способ Фалеса в указанном виде применим не всегда.
Учение о подобии фигур на основе теории отношений и пропорции было создано в
Древней Греции
в V- IV вв. до н. э. Оно изложено в VI книге «Начал» Евклида(III век до нашей эры), начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны»
3. Понятие подобных фигур.
В жизни мы встречаемся не только с равными фигурами, но и с такими, которые имеют одинаковую форму, но разные размеры. Геометрия называет такие фигуры подобными. Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника. Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.
Признаки подобия треугольников.
4. Измерительные работы с помощью подобия.
4.1. Определение высоты по тени.
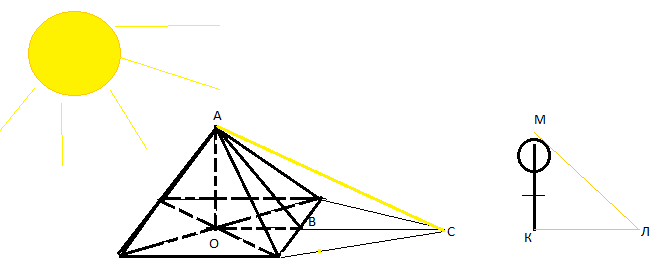
Я решила провести эксперимент по определению высоты по тени.
Для этого мне понадобились: фонарик, макет пирамиды, фигурка. Сделать миниатюрную пирамиду для проведения экспериментов несложно. Мне понадобились: лист бумаги; карандаш; линейка; ножницы; клей для бумаги. На листе бумаги я построила развертку пирамиды, в основании которой квадрат со стороной 7,6 см, а баковые грани – равные равнобедренные треугольники с боковой стороной 9,6 см. Высота получившейся пирамиды – 7,9 см. Высота фигурки 8,1 см. Попробуем измерить высоту данной пирамиды по её тени, используя также тень фигурки. В солнечный день я измерила тень пирамиды и фигурки. У меня получилось: 15см — тень фигурки, 13 см — тень пирамиды.
Построим геометрическую модель данной задачи:
, ∠
АСО=
∠
МЛК как углы падения солнечных лучей, значит по двум углам.
Найдем теперь высоту пирамиды другим способом для сравнения результатов. Найдем высоту боковой грани: АВ=
Из найдем высоту АО=
Мы получили практически одинаковые результаты. Получив такие результаты, я решила измерить высоту столба, выйдя на улицу.
Я выбрала столб, от которого падала четкая тень и измерила её. Она равнялась 21 м. Затем я стала рядом со столбом и мой помошник измерил мою тень, она равнялась 4,5 метра. Мой рост, учитывая, что я была в обуви и головном уборе, составил 1,6 .
Найдем высоту столба, составив геометрическую модель задачи.
Рассмотрим , КО – длина моей тени, ВС – длина тени столба. АВ – искомое.
∠АВС=∠МКО= как углы падения солнечных лучей.
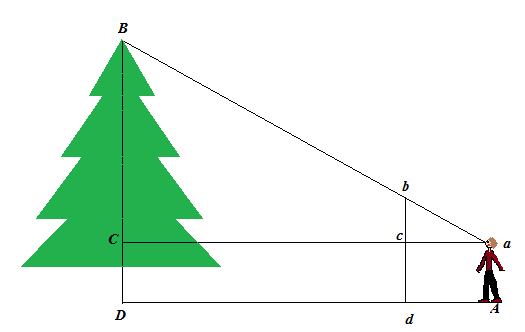
4.2. Измерение высоты пирамиды методом Жюля Верна.
«Таинственный остров» описывает интересный способ определения высоты: «Юноша, стараясь научиться возможно большему, последовал за инженером, который спустился с гранитной стены до окраины берега. Взяв прямой шест, футов 12 длиною, инженер измерил его возможно точнее, сравнивая со своим ростом, который был ему хорошо известен. Герберт же нес за ним отвес, врученный ему инженером: просто камень, привязанный к концу веревки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса Затем он отошел от шеста на такое расстояние, чтобы, лежа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. эту точку он тщательно пометил колышком.
Тебе знакомы начатки геометрии? — спросил он Герберта, поднимаясь с земли.
Помнишь свойства подобных треугольников?
Их сходственные стороны пропорциональны. — Правильно. Так вот: сейчас я построю два подобных прямоугольных треугольника. У меньшего одним катетом будет отвесный шест, другим — расстояние от колышка до основания шеста; гипотенуза же — мой луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же — мол луч зрения, совпадающий с направлением гипотенузы первого треугольника.
Понял!-воскликнул юноша.-Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены. — Да. И следовательно, если мы измерим два первых расстояния, то, зная высоту шеста, сможем вычислить четвертый, неизвестный член пропорции, т. е. высоту стены. Mы обойдемся, таким образом, без непосредственного измерении этой высоты. Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее — 500 футам. По окончании измерений инженер составил следующую запись:
4.3 Определение высоты с помощью высотомера
Высоту можно измерить специальным прибором — высотомером. Для изготовления данного прибора потребуется: Плотный белый картон, линейка, ручка, карандаш, ножницы, нитка, грузик, игла.
7. На нём с боков отгибаем два прямоугольника размером 3х5 см и прорезаем два отверстия с разным диаметром: одной поменьше — у глаза, другой побольше – для того, чтобы навести на вершину дерева. Итак, я решила провести эксперимент и проверить данный способ измерения высоты предмета. В качестве измеряемого объекта я выбрала дерево, растущее возле школы.
Я отошла от измеряемого предмета на 21 шаг, то есть EO =6,3 м. Я измерила показания прибора, он показывал 0,7. Мой рост 1,6 м. Требуется найти высоту дерева.
Для этого построим геометрическую модель данной задачи:
=
Прибавим к полученной величине мой рост и получим: ЛВ=ЛО+ОВ=3,71
1,6=5,31 – высота дерева.
Также, я могла допустить ошибки в использовании прибора Ошибки в использовании и изготовлении прибора:
1.Если не отгибать верхний прямоугольник от основания, то вы неправильно определите высоту.
2.При измерении высоты предмета, грузик должен быть направлен на конкретную величину разметки.
3.Расстояние от измеряемого объекта должно быть точным.
4.Точно наносить разметку в 1 см.
Эксперимент показал, что метод определения высоты предмета с помощью прибора «высомера» является более точным и удобным.
5. Выводы.
Литература
5. Перельман Я. И. Занимательная геометрия.– М.:Государственное издательство технико-теоретической литературы, 1950
Измерять высоту дерева можно 3-мя способами.
1. Общий
толковый словарь
русского языка [Электронный ресурс]. – Режим доступа: http://tolkslovar.ru/p22702.html
Просмотр содержимого документа
«Титульный лист»
Коммунальное учреждение «Общеобразовательная школа I
-III
ступеней №11 г.Енакиево»
«Математика вокруг нас»
Творческая работа на тему
«Подобие треугольников в реальной жизни»
Выполнила
ученица 8 класса
Сушко Дарья
Руководитель
учитель математики
Икаева Марина Александровна
Енакиево 2017
Просмотр содержимого презентации
«Подобие треугольников в реальной жизни»
КУ «Общеобразовательная школа І-ІІІ ступеней №11 г.Енакиево»
Конкурс ученических творческих проектов
«Математика вокруг нас»
Творческая работа на тему
«Подобие треугольников в реальной жизни»
Выполнила
ученица 8 класса
Сушко Дарья
Руководитель
учитель математики
Икаева Марина Александровна
Енакиево 2017
Целью моей работы было найти области применения подобия треугольников в реальной жизни.
Задачами моей работы были
- изучить литературу по данной теме;
- изучить историю возникновения понятия подобия;
- узнать, где применяется подобие треугольников;
- измерить высоту столба при помощи подобия треугольников различными способами;
Легенда об измерении Фалесом высоты пирамиды
В один из жарких дней Фалес вместе с главным жрецом храма Изиды прогуливался мимо пирамиды Хеопса.
Знает ли кто – либо, какова её высота?- спросил он.
Нет, сын мой, — ответил ему жрец,- древние папирусы не сохранили нам этого. — Но ведь определить высоту пирамиды можно совсем точно и прямо сейчас!- воскликнул Фалес.
Вот смотрите,- продолжал Фалес,- именно в это время, какой бы мы предмет не взяли, тень от него, если поставить его вертикально, точно высоте предмета!
Понятие
подобия
фигур
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника.
Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Измерение высоты по тени
Исходные данные задачи: Длина тени пирамиды ВС = 11 см, длина тени фигурки КЛ =15 см, высота фигурки КМ=8 см, основание пирамиды – квадрат со стороной 7,6 см. Высота пирамиды АО – искомое.
Рассмотрим
прямоугольные треугольники
АОС и МКЛ:
, ∠ АСО= ∠ МЛК как углы падения солнечных лучей, значит по двум углам.
Измерение высоты столба по его тени
Рассмотрим, КО – длина моей тени, ВС – длина тени столба. АВ – искомое.
∠ АВС=∠МКО= как углы падения солнечных лучей.
Таким образом, я получила приблизительное значение высоты столба 7,46 м.
Измерение высоты методом Жюль Верна
Этот метод заключается в том, что нужно вбить в землю шест, лечь на землю так, чтобы было видно верхний конец шеста и верхушку измеряемого предмета. Измерить расстояние от шеста до предмета, измерить высоту шеста и расстояние от макушки человека до основания шеста.
В романе Жюля Верна «Таинственный остров» Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее — 500 футам. По окончании измерений инженер составил следующую запись:
15: 500 = 10:х, 500 X 10 = 5000, 5000: 15 = 333,3.
Измерение высоты с помощью высотометра
1. Из картона чертим и вырезаем квадрат размером 15х15см.
2. Делим квадрат на два прямоугольника: 5х15 см, 10х15 см.
3. Прямоугольник 10х15 см делим на две части: 5 см и 10 см.
4. На большей части с длиной 10 см, наносим сантиметровые деления и обозначаем их
десятичной дробью
, то есть 0,1;0,2 и т.д.
5. В точке Е иглой делаем отверстие и протаскиваем нитку с грузиком, а затем закрепляем нитку сзади.
6. Для того, чтобы было удобнее смотреть, отгибаем верхний прямоугольник от основания.
7. На нём с боков отгибаем два прямоугольника размером 3х5 см и прорезаем два отверстия с разным диаметром: одной поменьше — у глаза, другой побольше – для того, чтобы навести на вершину дерева.
Измерение высоты с помощью высотометра
Чтобы найти высоту ЛВ нужно к ЛО прибавить свой рост.
ЛВ=ЛО+ОВ=3,71+1,6=5,31 – высота дерева.
Выводы:
Выполнив свою работу я узнала о том, что существуют много
различных способов
определения высоты предмета. Я провела эксперимент по определению высоты предмета по его тени. Испытание я проделала в домашних условиях на модели пирамиды и фигурки, а также на улице при измерении высоты столба. Также, я рассмотрела способ Жюля Верна для определения высоты. Я изучила понятие высотометра и изготовила прибор высотометр, который применила на практике для измерения высоты выбранного объекта. Самым
удобным способом
измерения высоты для меня пришлось использование высотометра. Таким образом, цели моей работы достигнуты. Можно смело утверждать, что подобие треугольников применяется в реальной жизни при измерительных работах на местности.
Литература:
1. Глейзер Г.И. История математики в школе. – М.:Издательство «Просвещение», 1964.
2.Перельман Я. И. Занимательная геометрия.– М.:Государственное издательство технико-теоретической литературы, 1950.
3.Ж.Верн. Таинственный остров.- М: Издательство « Детская литература», 1980.
4. Геометрия, 7 – 9: учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 18-е изд. – М.: Просвещение, 2010 Использованные материалы и интернет-ресурсы.
5. Перельман Я. И. Занимательная геометрия.– М.:Государственное издательство технико-теоретической литературы, 1950 Измерять высоту дерева можно 3-мя способами.
1. Общий толковый словарь русского языка [Электронный ресурс]. – Режим доступа:
http://tolkslovar.ru/p22702.html
2. Рисунок 2 [Электронный ресурс]. – Режим доступа: http://www.dopinfo.ru
СПАСИБО
Возможно, будет полезно почитать:
- Белецкий — значение и происхождение фамилии Руководствовался «флюидами неприязни»
; - Восточный гороскоп Какое сегодня год по японскому летоисчислению
; - Вредна ли шаурма Вредна ли шаурма для желудка
; - Сорбет из смородины в домашних условиях Как делать сорбет в домашних условиях
; - Как определить свежесть свинины
; - Чипсы в домашних условиях: готовим любимую хрустящую закуску без химии
; - Свиные ребрышки с картошкой
; - Салат с крабовыми палочками и корейской морковью
;
Частые вопросы
Где применяется подобие в жизни?
Например, картина и её фотография — это подобные фигуры. Карты одной и той же территории, сделанные в разных масштабах, подобны. Автомобиль и его модель — подобные тела, также любой макет подобен оригиналу, если сделан с соблюдением масштаба всех размеров.
В каком классе проходят Подобие треугольников?
Признаки подобия треугольников — урок. Геометрия, 8 класс.
Как объяснить Подобие треугольников?
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Кто придумал признаки подобия треугольников?
История Подобные фигуры рассматривались в Древней Греции в V—IV веках до нашей эры, они появляются в трудах Гиппократа Хиосского, Архита Тарентского, Евдокса Книдского и в VI книге «Начал» Евклида.
Полезные советы
СОВЕТ №1
При выполнении проектно-исследовательской работы по измерению высоты методом Жюля Верна, не забывайте о тщательной подготовке и калибровке используемых приборов. Точность измерений напрямую зависит от правильной настройки оборудования.
СОВЕТ №2
При выборе объекта для измерения высоты обратите внимание на его форму и структуру. Иногда необходимо учитывать не только прямую высоту, но и другие параметры, такие как наклон поверхности и ее неровности.