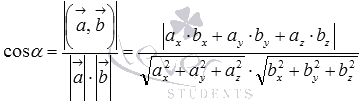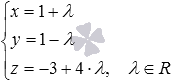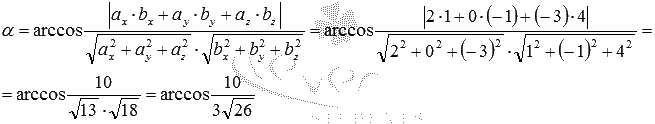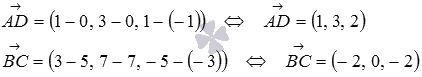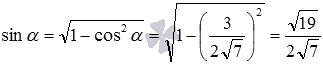Генетическая символика
Символика — перечень и объяснение условных названий и терминов, употребляемых в какой-либо отрасли науки.
Основы генетической символики были заложены Грегором Менделем, применившим буквенную символику для обозначения признаков. Доминантные признаки были обозначены заглавными буквами латинского алфавита А, В, С и т.д., рецессивные — малыми буквами — а, в, с и т.д. Буквенная символика, предложенная Менделем, по сути, алгебраическая форма выражения законов наследования признаков.
Для обозначения скрещивания принята следующая символика.
Родители обозначаются латинской буквой Р (Parents — родители), затем рядом записывают их генотипы. Женский пол обозначают сим волом ♂ (зеркало Венеры), мужской — ♀ (щит и копье Марса). Между родителями ставят знак «х», обозначающий скрещивание. Генотип женской особи пишут на первом месте, а мужской — на втором.
Первое по коление обозначается F
1
(Filli — дети), второе поколение — F
2
и т.д. Рядом приводят обозначения генотипов потомков.
Словарь основных терминов и понятий
Аллели (аллельные гены)
— разные формы одного гена, возникшие в результате мутаций и расположенные в одинаковых точках (локусах) парных гомологичных хромосом.
Альтернативные признаки
– взаимоисключающие, контрастные признаки.
Гаметы
(от греч. «
гаметес
» – супруг) – половая клетка растительного или животного организма, несущая один ген из аллельной пары. Гаметы всегда несут гены в «чистом» виде, т.к. образуются путем мейотического деления клеток и содержат одну из пары гомологичных хромосом.
Ген
(от греч. «
генос
» – рождение) – участок молекулы ДНК, несущий информацию о первичной структуре одного конкретного белка.
Гены аллельные
– парные гены, расположенные в идентичных участках гомологичных хромосом.
Генотип
— совокупность наследственных задатков (генов) организма.
Гетерозигота
(от греч. «
гетерос
» – другой и зигота) – зигота, имеющая два разных аллеля по данному гену (
Аа, Вb
).
Гетерозиготными
называют особей, получивших от родительских особей разные гены. Гетерозиготная особь в потомстве дает расщепление по данному признаку.
Гомозигота
(от греч. «
гомос
» – одинаковый и зигота) – зигота, имеющая одинаковые аллели данного гена (оба доминантные или оба рецессивные).
Гомозиготными
называют особей, получивших от родительских особей одинаковые наследственные задатки (гены) по какому-то конкретному признаку. Гомозиготная особь в потомстве не дает расщепления.
Гомологичные хромосомы
(от греч. «
гомос
» – одинаковый) – парные хромосомы, одинаковые по форме, размерам, набору генов. В диплоидной клетке набор хромосом всегда парный: одна хромосома из пары материнского происхождения, вторая – отцовская.
Гетерозиготными
называют особей, получивших от родительских особей разные гены. Таким образом, по генотипу особи могут быть гомозиготными (АА или аа) или гетерозиготными (Аа).
Доминантный признак (ген
) –
преобладающий, проявляющийся – обозначается заглавными буквами латинского алфавита:
А, В,
С и т. д.
Рецессивный признак (ген)
–
подавляемый признак – обозначается соответствующей строчной буквой латинского алфавита:
а, b с
и т. д
Скрещивание анализирующее
– скрещивание испытуемого организма с другим, являющимся по данному признаку рецессивной гомозиготой, что позволяет установить генотип испытуемого.
Скрещивание дигибридное
– скрещивание форм, отличающихся друг от друга по двум парам альтернативных признаков.
Скрещивание моногибридное
– скрещивание форм, отличающихся друг от друга по одной паре альтернативных признаков.
Чистые линии
–
организмы, гомозиготные по одному или нескольким признакам и не дающие в потомстве проявления альтернативного признака.
Фен
– признак.
Фенотип
— совокупность всех внешних признаков и свойств организма, до ступных наблюдению и анализу.
Алгоритм решения генетических задач
- Внимательно прочтите уровень задачи.
- Сделайте краткую запись условия задачи.
- Запишите генотипы и фенотипы скрещиваемых особей.
- Определите и запишите типы гамет, которые образуют скрещиваемые особи.
- Определите и запишите генотипы и фенотипы полученного от скрещивания потомства.
- Проанализируйте результаты скрещивания. Для этого определите количество классов потомства по фенотипу и генотипу и запишите их в виде числового соотношения.
- Запишите ответ на вопрос задачи.
(При решении задач по определённым темам последовательность этапов может изменяться, а их содержание модифицироваться.)
Оформление задач
- Первым принято записывать генотип женской особи, а затем – мужской (
верная запись — ♀ААВВ х ♂аавв; неверная запись
— ♂
аавв х ♀ААВВ). - Гены одной аллельной пары всегда пишутся рядом
(верная запись – ♀ААВВ; неверная запись ♀АВАВ). - При записи генотипа, буквы, обозначающие признаки, всегда пишутся в алфавитном порядке, независимо, от того, какой признак – доминантный или рецессивный – они обозначают (
верная запись — ♀ааВВ;
неверная запись -♀
ВВаа). - Если известен только фенотип особи, то при записи её генотипа пишут лишь те гены, наличие которых бесспорно.
Ген, который невозможно определить по фенотипу, обозначают значком «_»
(например, если жёлтая окраска (А) и гладкая форма (В) семян гороха – доминантные признаки, а зелёная окраска (а) и морщинистая форма (в) – рецессивные, то генотип особи с жёлтыми морщинистыми семенами записывают следующим образом:
А_вв
). - Под генотипом всегда пишут фенотип.
- Гаметы записывают, обводя их кружком
(А). - У особей определяют и записывают типы гамет, а не их количество
В этой статье сначала дадим определение угла между скрещивающимися прямыми и приведем графическую иллюстрацию. Далее ответим на вопрос: «Как найти угол между скрещивающимися прямыми, если известны координаты направляющих векторов этих прямых в прямоугольной системе координат»? В заключении попрактикуемся в нахождении угла между скрещивающимися прямыми при решении примеров и задач.
Навигация по странице.
Угол между скрещивающимися прямыми — определение.
К определению угла между скрещивающимися прямыми будем подходить постепенно.
Сначала напомним определение скрещивающихся прямых: две прямые в трехмерном пространстве называются
скрещивающимися, если они не лежат в одной плоскости. Из этого определения следует, что скрещивающиеся прямые не пересекаются, не параллельны, и, тем более, не совпадают, иначе они обе лежали бы в некоторой плоскости.
Приведем еще вспомогательные рассуждения.
Пусть в трехмерном пространстве заданы две скрещивающиеся прямые a
и b
. Построим прямые a 1
и b 1
так, чтобы они были параллельны скрещивающимся прямым a
и b
соответственно и проходили через некоторую точку пространства M 1
. Таким образом, мы получим две пересекающиеся прямые a 1
и b 1
. Пусть угол между пересекающимися прямыми a 1
и b 1
равен углу . Теперь построим прямые a 2
и b 2
, параллельные скрещивающимся прямым a
и b
соответственно, проходящие через точку М 2
, отличную от точки М 1
. Угол между пересекающимися прямыми a 2
и b 2
также будет равен углу . Это утверждение справедливо, так как прямые a 1
и b 1
совпадут с прямыми a 2
и b 2
соответственно, если выполнить параллельный перенос, при котором точка М 1
перейдет в точку М 2
. Таким образом, мера угла между двумя пересекающимися в точке М
прямыми, соответственно параллельными заданным скрещивающимся прямым, не зависит от выбора точки М
.
Теперь мы готовы к тому, чтобы дать определение угла между скрещивающимися прямыми.
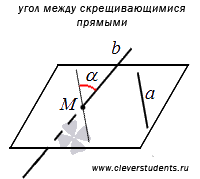
Определение.
Угол между скрещивающимися прямыми– это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.
Из определения следует, что угол между скрещивающимися прямыми также не будет зависеть от выбора точки M
. Поэтому в качестве точки М
можно взять любую точку, принадлежащую одной из скрещивающихся прямых.
Приведем иллюстрацию определения угла между скрещивающимися прямыми.
Мнение эксперта:
Скрещивающиеся прямые — это одна из основных тем в геометрии, которая часто встречается в школьных задачах и в реальной жизни. Эксперты отмечают, что понимание этой концепции является важным элементом математической грамотности. Примеры задач с решениями помогают учащимся усвоить этот материал, развивая их логическое мышление. Однако, также важно предоставлять и примеры задач без решений, чтобы стимулировать самостоятельное мышление и поиск альтернативных подходов к решению проблемы. Такой подход способствует формированию навыков анализа и поиска решений, что является важным в современном мире.

Нахождение угла между скрещивающимися прямыми.
Так как угол между скрещивающимися прямыми определяется через угол между пересекающимися прямым, то нахождение угла между скрещивающимися прямыми сводится к нахождению угла между соответствующими пересекающимися прямыми в трехмерном пространстве.
Несомненно, для нахождения угла между скрещивающимися прямыми подходят методы, изучаемые на уроках геометрии в средней школе. То есть, выполнив необходимые построения, можно связать искомый угол с каким-либо известным из условия углом, основываясь на равенстве или подобии фигур, в некоторых случаях поможет
теорема косинусов
, а иногда к результату приводит
определение синуса, косинуса и тангенса угла
прямоугольного треугольника.
Однако очень удобно решать задачу нахождения угла между скрещивающимися прямыми методом координат. Именно его и рассмотрим.
Пусть в трехмерном пространстве введена Oxyz
(правда, во многих задачах ее приходится вводить самостоятельно).
Поставим перед собой задачу: найти угол между скрещивающимися прямыми a
и b
, которым соответствуют в прямоугольной системе координат Oxyz
некоторые уравнения прямой в пространстве .
Решим ее.
Возьмем произвольную точку трехмерного пространства М
и будем считать, что через нее проходят прямые a 1
и b 1
, параллельные скрещивающимся прямым a
и b
соответственно. Тогда искомый угол между скрещивающимися прямыми a
и b
равен углу между пересекающимися прямыми a 1
и b 1
по определению.
Таким образом, нам осталось найти угол между пересекающимися прямыми a 1
и b 1
. Чтобы применить формулу для нахождения угла между двумя пересекающимися прямыми в пространстве нам нужно знать координаты направляющих векторов прямых a 1
и b 1
.
Как же мы их можем получить? А очень просто. Определение направляющего вектора прямой позволяет утверждать, что множества направляющих векторов параллельных прямых совпадают. Следовательно, в качестве направляющих векторов прямых a 1
и b 1
можно принять направляющие векторы
и
прямых a
и b
соответственно.
Итак,
угол между двумя скрещивающимися прямыми a
и b
вычисляется по формуле
, где
и
— направляющие векторы прямых a
и b
соответственно.
Формула для нахождения косинуса угла между скрещивающимися прямымиa
и b
имеет вид
.
Позволяет найти синус угла между скрещивающимися прямыми, если известен косинус:
.
Осталось разобрать решения примеров.
Пример.
Найдите угол между скрещивающимися прямыми a
и b
, которые определены в прямоугольной системе координат Oxyz
уравнениями
и
.
Решение.
Канонические уравнения прямой в пространстве позволяют сразу определить координаты направляющего вектор этой прямой – их дают числа в знаменателях дробей, то есть,
. Параметрические уравнения прямой в пространстве также дают возможность сразу записать координаты направляющего вектора – они равны коэффициентам перед параметром, то есть,
— направляющий вектор прямой
. Таким образом, мы располагаем всеми необходимыми данными для применения формулы, по которой вычисляется угол между скрещивающимися прямыми:
Ответ:
Угол между заданными скрещивающимися прямыми равен .
Пример.
Найдите синус и косинус угла между скрещивающимися прямыми, на которых лежат ребра AD
и BC
пирамиды АВСD
, если известны координаты ее вершин: .
Решение.
Направляющими векторами скрещивающихся прямых AD
и BC
являются векторы и . Вычислим их координаты как разность соответствующих координат точек конца и начала вектора:
По формуле
мы можем вычислить косинус угла между указанными скрещивающимися прямыми:
Теперь вычислим синус угла между скрещивающимися прямыми:
Интересные факты
- Скрещивающиеся прямые — это две прямые, которые пересекаются в одной точке. Угол между скрещивающимися прямыми всегда меньше 180 градусов.
Пример задачи:
Найдите угол между скрещивающимися прямыми AB и CD, если известно, что угол между AB и AC равен 30 градусов, а угол между CD и AC равен 45 градусов.
Решение:
Угол между AB и CD равен 180 — (30 + 45) = 105 градусов.
- Скрещивающиеся прямые образуют четыре угла. Эти углы называются смежными углами. Смежные углы всегда в сумме дают 180 градусов.
Пример задачи:
Найдите углы, образованные скрещивающимися прямыми AB и CD, если известно, что угол между AB и AC равен 30 градусов.
Решение:
Углы, образованные скрещивающимися прямыми AB и CD, равны 30, 150, 30 и 150 градусов.
- Скрещивающиеся прямые образуют четыре треугольника. Эти треугольники называются смежными треугольниками. Смежные треугольники всегда имеют одну общую сторону и два общих угла.
Пример задачи:
Найдите площадь смежного треугольника ABC, если известно, что стороны AB и AC равны 5 и 6 см соответственно, а угол между ними равен 30 градусов.
Решение:
Площадь смежного треугольника ABC равна 15 квадратных сантиметров.

Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A
B
C
точка 1, точка 2, точка 3
1
2
3
Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие?
A
A
A
Опыт других людей
Скрещивающиеся прямые — одна из основных тем в геометрии, вызывающая много вопросов у школьников и студентов. Многие отмечают, что понимание этой темы помогает им лучше освоить материал по геометрии и применять его на практике. Примеры задач с решениями помогают увидеть, как применять знания о скрещивающихся прямых на практике и развивать логическое мышление. Благодаря этим задачам студенты улучшают свои навыки в решении геометрических задач и увереннее сдают экзамены.

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a
b
c
Линия может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
a
прямая линия AB
B
A
Прямые могут быть
- пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча
A
A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
a
луч AB
B
A
Лучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C
B
A
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B
A
прямая линия AB
B
A
От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
✂
B
A
✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B
A
Задача: где прямая
, луч
, отрезок
, кривая
?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A
B
C
D
E
64
62
127
52
Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача:
какая ломанная длиннее
, а
у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A
B
C
D
E
F
120
60
58
122
98
141
Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.д.
На лекционных и практических занятиях будет принята система обозначений и символики (табл. 2,3), разработанная проф. Н.Ф.Четверухиным. Система этих обозначений широко применяется в настоящее время кафедрами начертательной геометрии и инженерной графики ведущих вузов России.
Таблица 2
ОБОЗНАЧЕНИЯ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
| Геометрическая фигура (объект) | Обозначение и пример |
| Точка | Прописная буква латинского алфавита: А, В, С, … или арабская цифра: 1, 2, 3, … (может быть римская цифра: I, II, III, …). Центр проецирования S. Начало координат О(буква). Точка в бесконечности: S ¥, А¥ , В¥ , …. |
| Линия – прямая или кривая | Строчная буква латинского алфавита: a, b, c, …. Горизонталь h; фронталь f; профильная прямая или кривая (профиль) р; ось вращения i; направление проецирования или направление взгляда в пространстве: s– на П 1, v– на П 2; оси координат: x, y, z; оси проекций x, y, zили x 12, x 24и т.д. ( АВ) – прямая, определяемая точками Аи В; Ι АВΙ – длина отрезка АВ, натуральная величина отрезка АВ. Скобки не даются, если в тексте имеются соответствующие слова (например, прямая АВ). |
| Поверхность (включая плоскость) |
Г(гамма), S(сигма), L(лямбда), …. |
| Плоскость проекций | Прописная буква греческого алфавита: П(пи) с добавлением индекса. П 1– горизонтальная плоскость проекций; П 2– фронтальная плоскость проекций; П 3– профильная плоскость проекций; П 4, П 5, … – дополнительные плоскости проекций. |
| Угол | Строчная буква греческого алфавита: a, b, g, …. |
| Проекция объекта |
А 1, b 1, S 1– горизонтальные проекции точки А, линии b, поверхности S; А 2, b 2, S 2– фронтальные проекции точки А, прямой b, поверхности S; и т.д. |
Таблица 3
СИМВОЛЫ ВЗАИМОРАСПОЛОЖЕНИЯ И ЛОГИЧЕСКИХ ОПЕРАЦИЙ
| Знак | Смысл знака | Пример, пояснение |
| Ì или É Î или « |
Взаимная принадлежность (инцидентность) объектов как множеств, подмножеств Взаимная принадлежность (инцидентность) объектов, из которых один – множество, другой – элемент множества, т.е. точка |
tÌ Г– линия tпринадлежит поверхности Г; поверхность Гпроходит через линию t; ГÉ t– то же (знак открытой частью всегда обращен в сторону большего множества). t»А– линия tпроходит через точку А; точка Апринадлежит линии t; АÎ t– то же (знак Î открытой частью обращен в сторону множества). |
| ∩ | Пересечение |
а∩ b– линии aи bпересекаются; S( a∩ b) – плоскость Sзадана пересекающимися прямыми aи b. |
| = или |
Результат Равенство Совпадение |
А= а∩ b– точка Аполучена в результате пересечения линий aи b.ê АВê=ê ЕFê– отрезок АВравен отрезку ЕF. А 2= В 2– фронтальные проекции точек Аи Всовпадают. |
| ΙΙ | Параллельность | ( АВ) ΙΙ (СD) – прямые АВи СDпараллельны. |
| ^ | Перпендикулярность |
АВ^ СD |
| ® | Отображается, последовательность действий |
А1 ® А2 – по горизонтальной проекции точки Астроим фронтальную. |
4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ГРАФИЧЕСКИХ РАБОТ
Графическая работа № 1
«Проецирование»
Задание:
1.На формате А3 по двум заданным проекциям домика построить профильную проекцию, увеличив изображение в 2 раза.
2.Определить на чертеже, обозначить и записать в таблице в правом нижнем углу (размер таблицы – 100х100 мм), расположенной над основной надписью, положение прямых в пространстве (прямую общего положения, три линии уровня, три проецирующие прямые, одну пару параллельных прямых, одну пару пересекающихся прямых, одну пару скрещивающихся прямых).
3.Определить натуральную величину прямой общего положения и углы наклона ее к плоскостям проекций.
4.Определить координаты любых пяти обозначенных точек. Данные внести в таблицу в правом верхнем углу формата (размер таблицы 40х60 мм).
5.Выбрать и построить на формате А4 аксонометрическую проекцию домика, начертить схему аксонометрических осей. Аксонометрию затонировать цветными карандашами.
Указания к выполнению графической работы №1. На листе формата А3 провести оси координат в центре листа. Согласно своему варианту построить две проекции «Домика», увеличив изображение в 2 раза. Фронтальная проекция основания «домика» должна находиться на оси ОХ. С помощью линий проекционной связи построить третью проекцию «домика».
Далее последовательно определить и обозначить заглавными буквами латинского алфавита на трех проекциях «домика» прямые, указанные в задании. Полученные результаты внести в таблицу. Образец заполнения таблицы приведен на рисунке.
Для найденной прямой общего положения на плоскости П 1 и П 2 определить и обозначить натуральную величину способом прямоугольного треугольника и углы наклона ее к горизонтальной и фронтальной плоскостям проекций (α и β).
Для любых пяти обозначенных точек определить координаты. Значения в мм занести в таблицу. Образец заполнения таблицы приведен на рисунке.
Выбрать вид аксонометрической проекции таким образом, чтобы на изображении домика плоскости (грани) не проецировались в линии. На формате А4 построить выбранную аксонометрическую проекцию, сохраняя вторичную горизонтальную проекцию и аксонометрические оси.
С помощью цветных карандашей выполнить тонировку аксонометрической проекции «Домика». В правом верхнем углу начертить схему аксонометрических осей. Пример графической работы на рисунке 9,10.
Варианты заданий к графической работе №1 «Проецирование»
Графическая работа № 2
«Построение усеченной призмы и усеченного цилиндра»
Задание:
Графическая работа выполняется на двух форматах А3, и состоит из двух задач.
Задача №1. Построить три проекции прямой шестигранной призмы (данные для построения взять из таблицы по своему варианту). Построить натуральную величину контура сечения применив способом замены плоскостей проекций. Построить развертку. Выбрать и начертить аксонометрическую проекцию. Размеры не наносить. На чертеже должны быть обозначены точки для построения и линии проекционной связи.
Возможно, будет полезно почитать:
- Заявление о приостановке работы в связи с невыплатой зарплаты
; - Что сказано об увольнении по собственному желанию в п
; - Как восстановить утерянную квитанцию Потерял чек сбербанка можно ли восстановить
; - Где взять номер лицевого счета для заявления на налоговый вычет?
; - Порядок заполнения перечня заявлений о ввозе товаров и уплате косвенных налогов Проверить уплату косвенных налогов в белоруссии
; - Поиск инн организации по названию
; - Дистанционное обучение на бухгалтерских курсах
; - Измерение величин Измеряется s в физике
;
Частые вопросы
Какие прямые называются скрещивающимися приведите примеры?
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. Две скрещивающиеся прямые Две скрещивающиеся прямые (красные) в первом октанте и их общий перпендикуляр (синий).
Как определить что прямые скрещивающиеся?
Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Как построить угол между скрещивающимися прямыми?
Чтобы найти угол между скрещивающимися прямыми, нужно знать, что через каждую из двух скрещивающихся прямых можно провести плоскость, параллельную второй прямой, при том только одну. Чтобы найти угол между скрещивающимися прямыми, нужно найти угол между одной прямой и проекцией другой прямой.
Как найти расстояние между двумя скрещивающимися прямыми?
- Строим плоскость, перпендикулярную одной из скрещива- ющихся прямых. 2) Находим проекции этих прямых на данную плоскость. 3) Проекция одной из этих прямых на эту плоскость является точкой. Вычисляем расстояние от этой точки до проекции другой прямой на эту плоскость.
Полезные советы
СОВЕТ №1
Перед тем, как приступить к решению задач на скрещивающиеся прямые, важно освежить знания о свойствах углов и прямых. Повторите определения вертикальных углов, смежных углов, углов, образованных параллельными прямыми и трансверсальной, а также другие основные понятия.
СОВЕТ №2
При решении задач с прямыми не забывайте использовать свойства параллельных и пересекающихся прямых, такие как равенство углов при параллельных прямых, сумма углов в треугольнике, вертикальные углы и т.д. Это поможет вам найти правильное решение задачи.