В чем заключается парадокс близнецов. Парадокс близнецов (мысленный эксперимент): объяснение

8. Парадокс близнецов

Какова была реакция всемирно известных ученых и философов на странный,
новый мир
относительности? Она была различной. Большинство физиков и астрономов, смущенные нарушением «здравого смысла» и математическими трудностями общей теории относительности, хранили благоразумное молчание. Но ученые и философы, способные понять теорию относительности, встретили ее с радостью. Мы уже упоминали, как быстро Эддингтон осознал важность достижений Эйнштейна. Морис Шлик, Бертран Рассел, Рудольф Кернэп, Эрнст Кассирер, Альфред Уайтхед, Ганс Рейхенбах и многие другие выдающиеся философы были первыми энтузиастами, которые писали об этой теории и старались выяснить все ее следствия. Книга Рассела «Азбука теории относительности» была впервые опубликована в 1925 г., но до сих пор она остается одним из лучших популярных изложений теории относительности.

Многие ученые оказались неспособными освободиться от старого, ньютоновского образа мыслей.

Они во многом напоминали ученых далеких дней Галилея, которые не могли заставить себя признать, что Аристотель мог ошибаться. Сам Майкельсон, знания математики которого были ограниченными, так и не признал теории относительности, хотя его великий эксперимент проложил путь специальной теории. Позже, в 1935 г., когда я был студентом Чикагского университета, курс астрономии читал нам профессор Вильям Макмиллан, широко известный ученый. Он открыто говорил, что теория относительности – это печальное недоразумение.

«

Мы, современное поколение, слишком нетерпеливы, чтобы чего-нибудь дождаться», – писал Макмиллан в 1927 г. «

За сорок лет, прошедших после попытки Майкельсона обнаружить ожидавшееся движение Земли относительно эфира, мы отказались от всего, чему нас учили раньше, создали постулат, самый бессмысленный из всех, который мы только смогли придумать, и создали неньютоновскую механику, согласующуюся с этим постулатом. Достигнутый успех – превосходная дань нашей умственной активности и нашему остроумию, но нет уверенности, что нашему здравому смыслу».

Самые разнообразные возражения выдвигались против теории относительности. Одно из наиболее ранних и наиболее упорных возражений высказывалось относительно парадокса, впервые упомянутого самим Эйнштейном в 1905 г. в его статье о специальной теории относительности (слово «парадокс» употребляется для обозначения чего-то противоположного общепринятому, но логически непротиворечивого).

Этому парадоксу уделяется много внимания в современной
научной литературе
, поскольку развитие космических полетов наряду с конструированием фантастически точных приборов для измерения времени может вскоре дать способ проверки этого парадокса прямым способом.

Этот парадокс обычно излагается как мысленный опыт с участием близнецов. Они сверяют свои часы. Один из близнецов на космическом корабле совершает длительное путешествие в космосе. Когда он возвращается, близнецы сравнивают показания часов. Согласно специальной теории относительности часы путешественника покажут несколько меньшее время. Другими словами, время в космическом корабле движется медленнее, чем на Земле.

До тех пор, пока космический маршрут ограничен солнечной системой и совершается с относительно малой скоростью, эта разница времен будет пренебрежимо малой. Но на больших расстояниях и при скоростях, близких к скорости света, «сокращение времени» (так иногда называют это явление) будет возрастать. Нет ничего невероятного в том, что со временем будет открыт способ, с помощью которого космический корабль, медленно ускоряясь, сможет достичь скорости, лишь немного меньшей скорости света. Это даст возможность посещать другие звезды в нашей Галактике, а возможно, даже и другие галактики. Итак, парадокс близнецов – больше чем просто головоломка для гостиной, когда-нибудь он станет повседневностью космических путешественников.

Допустим, что космонавт – один из близнецов – проходит расстояние в тысячу световых лет и возвращается: это расстояние мало по сравнению с размерами нашей Галактики. Есть ли уверенность, что космонавт не умрет задолго до конца пути? Не потребуется ли для его путешествия, как во многих научно-фантастических произведениях, целой колонии мужчин и женщин, поколениями живущих и умирающих, пока корабль совершает свое длинное межзвездное путешествие?

Ответ зависит от скорости движения корабля.

Если путешествие будет происходить со скоростью, близкой к скорости света, время внутри корабля будет течь много медленней. По земному времени путешествие будет продолжаться, конечно, более 2000 лет. С точки зрения космонавта, в корабле, если он движется достаточно быстро, путешествие может продлиться лишь несколько десятилетий!

Для тех читателей, которые любят численные примеры, приведем результат недавних расчетов Эдвина Макмиллана, физика из Калифорнийского университета в Беркли. Некий космонавт отправился с Земли к спиральной туманности Андромеды.

До нее немного меньше двух миллионов световых лет. Космонавт первую половину дороги проходит с постоянным ускорением 2g, затем с постоянным замедлением в 2g вплоть до достижения туманности. (Это
удобный способ
создания постоянного поля тяготения внутри корабля на все время длинного путешествия без помощи вращения.) Обратный путь совершается тем же способом. Согласно собственным часам космонавта продолжительность путешествия составит 29 лет. По земным часам пройдет почти 3 миллиона лет!

Вы сразу заметили, что возникают самые разнообразные привлекательные возможности. Сорокалетний ученый и его юная лаборантка влюбились друг в друга. Они чувствуют, что разница в возрасте делает их свадьбу невозможной. Поэтому он отправляется в длинное космическое путешествие, передвигаясь со скоростью, близкой к скорости света. Он возвращается в возрасте 41 года. Тем временем его подруга на Земле стала тридцатитрехлетней женщиной. Вероятно, она не смогла ждать возвращения любимого 15 лет и вышла замуж за кого-то другого. Ученый не может вынести этого и отправляется в другое продолжительное путешествие, тем более что ему интересно выяснить отношение последующих поколений к одной, созданной им теории, подтвердят они ее или опровергнут. Он возвращается на Землю в возрасте 42 лет. Подруга его прошлых лет давно умерла, и, что еще хуже, от его столь дорогой ему теории ничего не осталось. Оскорбленный, он отправляется в еще более
длинный путь
, чтобы, возвратившись в возрасте 45 лет, увидеть мир, проживший уже несколько тысячелетий. Возможно, что, подобно путешественнику из романа Уэллса «Машина времени», он обнаружит, что человечество выродилось. И вот тут он «сядет на мель». «Машина времени» Уэллса могла передвигаться в обоих направлениях, а у нашего одинокого ученого не будет способа вернуться обратно в привычный ему отрезок человеческой истории.

Если такие путешествия во времени станут возможными, то возникнут совершенно необычные моральные вопросы. Будет ли что-нибудь незаконного в том, например, что женщина вышла замуж за собственного пра-пра-пра-пра-пра-правнука?

Заметьте, пожалуйста: этот сорт путешествий во времени обходит все логические ловушки (этот бич научной фантастики), как, например, возможность попасть в прошлое и убить
собственных родителей
до вашего появления на свет или юркнуть в будущее и подстрелить самого себя, послав пулю в лоб.

Рассмотрим, например, положение с мисс Кэт из известного шуточного стишка:

Юная леди по имени Кэт

Двигалась много быстрее, чем свет.

Но попадала всегда не туда:

Быстро помчишься – придешь во вчера.

Перевод А. И. Базя

Возвратись она вчера, она должна была бы встретиться со своим двойником. В противном случае это не было бы действительно вчера. Но вчера не могло быть двух мисс Кэт, поскольку, отправляясь в путешествие во времени, мисс Кэт ничего не помнила о своей встрече со своим двойником, состоявшейся вчера. Итак, перед вами логическое противоречие. Такого типа путешествия во времени невозможны логически, если не предполагать существования мира, идентичного нашему, но движущегося по другому пути во времени (на день раньше). Даже при этом положение дел очень усложняется.

Заметьте также, что эйнштейновская форма путешествий во времени не приписывает путешественнику какого-то подлинного бессмертия или хотя бы долголетия. С точки зрения путешественника, старость подходит к нему всегда с нормальной скоростью. И лишь «собственное время» Земли кажется этому путешественнику несущимся с головокружительной скоростью.

Анри Бергсон, известный французский философ, был наиболее выдающимся из мыслителей, скрестивших шпаги с Эйнштейном из-за парадокса близнецов. Он много писал об этом парадоксе, потешаясь над тем, что казалось ему логически абсурдным. К сожалению, все им написанное доказало лишь то, что можно быть крупным философом без заметных знаний математики. В последние несколько лет протесты появились снова. Герберт Дингль,
английский физик
, «наиболее громко» отказывается поверить в парадокс. Уже немало лет он пишет остроумные статьи об этом парадоксе и обвиняет специалистов по теории относительности то в тупости, то в изворотливости. Поверхностный анализ, который будет проведен нами, конечно, не разъяснит полностью идущую полемику, участники которой быстро углубляются в сложные уравнения, но поможет уяснить общие причины, приведшие к почти единодушному признанию специалистами того, что парадокс близнецов будет осуществляться именно так, как написал об этом Эйнштейн.

Возражение Дингля, наиболее сильное из когда-либо выдвинутых против парадокса близнецов, заключается в следующем. Согласно общей теории относительности не существует никакого абсолютного движения, нет «избранной» системы отсчета.

Всегда можно выбрать движущийся предмет за неподвижную систему отсчета, не нарушая при этом никаких законов природы. Когда за систему отсчета принята Земля, то космонавт совершает длительное путешествие, возвращается и обнаруживает, что стал моложе брата-домоседа. А что произойдет, если систему отсчета связать с космическим кораблем? Теперь мы должны считать, что Земля проделала длительное путешествие и возвратилась назад.

В этом случае домоседом будет тот из близнецов, который находился в космическом корабле. Когда Земля возвратится, не станет ли брат, находившийся на ней, моложе? Если так произойдет, то в создавшемся положении парадоксальный вызов здравому смыслу уступит место очевидному логическому противоречию. Ясно, что каждый из близнецов не может быть моложе другого.

Дингль хотел бы сделать из этого вывод: или необходимо предположить, что по окончании путешествия возраст близнецов будет в точности одинаков, или принцип относительности должен быть отброшен.

Не выполняя никаких вычислений, нетрудно понять, что кроме этих двух альтернатив существуют и другие. Верно, что всякое движение относительно, но в
данном случае
имеется одно, очень важное различие между относительным движением космонавта и относительным движением домоседа. Домосед неподвижен относительно Вселенной.

Как эта разница сказывается на парадоксе?

Допустим, что космонавт отправляется проведать планету X где-то в Галактике. Его путешествие проходит при постоянной скорости. Часы домоседа связаны с инерциальной системой отсчета Земли, и их показания совпадают с показаниями всех остальных часов на Земле потому, что все они неподвижны по отношению друг к другу. Часы космонавта связаны с другой инерциальной системой отсчета, с кораблем. Если бы корабль постоянно придерживался одного направления, то не возникло бы никакого парадокса вследствие того, что не было бы никакого способа сравнить показания обоих часов.

Но у планеты X корабль останавливается и поворачивает обратно. При этом инерциальная система отсчета изменяется: вместо системы отсчета, движущейся от Земли, появляется система, движущаяся к Земле. При таком изменении возникают громадные силы инерции, поскольку при повороте корабль испытывает ускорение. И если ускорение при повороте будет очень большим, то космонавт (а не его брат-близнец на Земле) погибнет. Эти силы инерции возникают, конечно, из-за того, что космонавт ускоряется по отношению к Вселенной. Они не возникают на Земле, потому что Земля не испытывает такого ускорения.

С одной точки зрения, можно было бы сказать, что силы инерции, созданные ускорением, «вызывают» замедление часов космонавта; с другой точки зрения, возникновение ускорения просто обнаруживает изменение системы отсчета. Вследствие такого изменения мировая линия космического корабля, его путь на графике в четырехмерном пространстве – времени Минковского изменяется так, что полное «собственное время» путешествия с возвратом оказывается меньше, чем полное собственное время вдоль мировой линии близнеца-домоседа. При изменении системы отсчета участвует ускорение, но в расчет входят только уравнения специальной теории.

Возражение Дингля все еще сохраняется, так как точно те же вычисления можно было бы проделать и при предположении, что неподвижная система отсчета связана с кораблем, а не с Землей. Теперь в путь отправляется Земля, затем она возвращается обратно, меняя инерциальную систему отсчета. Почему бы не проделать те же вычисления и на основе тех же уравнений не показать, что время на Земле отстало? И эти вычисления были бы справедливы, не будь одного необычайной важности факта: при движении Земли вся Вселенная двигалась бы вместе с нею. При повороте Земли поворачивалась бы и Вселенная. Это ускорение Вселенной создало бы мощное гравитационное поле. А как уже было показано, тяготение замедляет часы. Часы на Солнце, например, тикают реже, чем такие же часы на Земле, а на Земле реже, чем на Луне. После выполнения всех расчетов оказывается, что гравитационное поле, созданное ускорением космоса, замедлило бы часы в космическом корабле по сравнению с земными в точности на столько же, на сколько они замедлялись в предыдущем случае. Гравитационное поле, конечно, не повлияло на земные часы. Земля неподвижна относительно космоса, следовательно, на ней и не возникало дополнительного гравитационного поля.

Поучительно рассмотреть случай, при котором возникает точно такая же разница во времени, хотя никаких ускорений нет. Космический корабль А пролетает мимо Земли с постоянной скоростью, направляясь к планете X. В момент прохождения корабля мимо Земли часы на нем устанавливаются на ноль. Корабль А продолжает свое движение к планете X и проходит мимо космического корабля Б, движущегося с постоянной скоростью в противоположном направлении. В момент наибольшего сближения корабль А по радио сообщает кораблю Б время (измеренное по своим часам), прошедшее с момента пролета им мимо Земли. На корабле Б запоминают эти сведения и продолжают с постоянной скоростью двигаться к Земле. Проходя мимо Земли, они сообщают на Землю сведения о времени, затраченном А на путешествие с Земли до планеты X, а также время, затраченное Б (и измеренное по его часам) на путешествие от планеты X до Земли. Сумма этих двух промежутков времени будет меньше, чем время (измеренное по земным часам), протекшее с момента прохождения А мимо Земли до момента прохождения Б.

Эта разница во времени может быть вычислена по уравнениям специальной теории. Никаких ускорений здесь не было. Конечно, в данном случае нет и парадокса близнецов, поскольку нет космонавта, улетевшего и возвратившегося назад. Можно было бы предположить, что путешествующий близнец отправился на корабле А, затем пересел на корабль Б и вернулся обратно; но этого нельзя сделать без перехода от одной инерциальной системы отсчета к другой. Чтобы сделать такую пересадку, он должен был бы подвергнуться действию потрясающе
мощных сил
инерции. Эти силы вызывались бы тем, что изменилась его система отсчета. При желании мы могли бы сказать, что силы инерции замедлили часы близнеца. Однако если рассматривать весь эпизод с точки зрения путешествующего близнеца, связав его с неподвижной системой отсчета, то в рассуждения войдет сдвигающийся космос, создающий гравитационное поле. (Главный источник путаницы при рассмотрении парадокса близнецов заключается в том, что положение может быть описано с разных точек зрения.) Независимо от принятой точки зрения уравнения теории относительности всегда дают одну и ту же разницу во времени. Эту разницу можно получить, пользуясь одной лишь специальной теорией. И вообще для обсуждения парадокса близнецов мы привлекли общую теорию лишь для того, чтобы опровергнуть возражения Дингля.

Часто бывает невозможно установить, какая из возможностей «правильная». Путешествующий близнец летает туда и обратно или это проделывает домосед вместе с космосом? Есть факт: относительное движение близнецов. Имеется, однако, два
различных способа
рассказать об этом. С одной точки зрения, изменение инерциальной системы отсчета космонавта, создающее силы инерции, приводит к разнице в возрасте. С другой точки зрения, действие сил тяготения перевешивает эффект, связанный с изменением Землей инерциальной системы. С любой точки зрения домосед и космос неподвижны по отношению друг к другу. Итак, положение полностью различно с разных точек зрения, несмотря на то что относительность движения строго сохраняется. Парадоксальная разница в возрасте объясняется независимо от того, какой из близнецов считается покоящимся. Нет необходимости отбрасывать теорию относительности.

А теперь может быть задан интересный вопрос.

Что, если в космосе нет ничего, кроме двух
космических кораблей
, А и Б? Пусть корабль А, используя свой ракетный двигатель, ускорится, совершит длинное путешествие и вернется назад. Будут ли предварительно синхронизированные часы на обоих кораблях вести себя по-прежнему?

Ответ будет зависеть от того, чьего взгляда на инерцию вы придерживаетесь – Эддингтона или Денниса Скьяма. С точки зрения Эддингтона – «да». Корабль А ускоряется по отношению к пространственно-временной метрике космоса; корабль Б – нет. Их поведение несимметрично и приведет к обычной разнице в возрасте. С точки зрения Скьяма- «нет». Имеет смысл говорить об ускорении только по отношению к другим материальным телам. В данном случае единственными предметами являются два космических корабля. Положение полностью симметрично. И действительно, в данном случае нельзя говорить об инерциальной системе отсчета потому, что нет инерции (кроме крайне слабой инерции, созданной присутствием двух кораблей). Трудно предсказать, что случилось бы в космосе без инерции, если бы корабль включил свои
ракетные двигатели
! Как выразился с английской осторожностью Скьяма: «Жизнь была бы совсем другой в такой Вселенной!»

Поскольку замедление часов путешествующего близнеца можно рассматривать как гравитационное явление, любой опыт, который показывает замедление времени под действием тяжести, представляет собой косвенное подтверждение парадокса близнецов. В
последние годы
было получено несколько таких подтверждений с помощью нового замечательного лабораторного метода, основанного на эффекте Мёссбауэра. Молодой немецкий физик Рудольф Мёссбауэр в 1958 г. открыл способ изготовления «ядерных часов», с непостижимой точностью отмеряющих время. Представьте часы, «тикающие пять раз в секунду, и другие часы, тикающие так, что после миллиона миллионов тиканий они отстанут лишь на одну сотую тиканья. Эффект Мёссбауэра способен сразу же обнаружить, что вторые часы идут медленнее первых!

Опыты с применением эффекта Мёссбауэра показали, что время вблизи фундамента здания (где тяжесть больше) течет несколько медленнее, чем на его крыше. По замечанию Гамова: «Машинистка, работающая на первом этаже здания Эмпайр Стейт Билдинг, старится медленнее, чем ее сестра-близнец, работающая под самой крышей». Конечно, эта разница в возрасте неуловимо мала, но она есть и может быть измерена.

Английские физики, используя эффект Мёссбауэра, обнаружили, что ядерные часы, помещенные на краю быстро вращающегося диска диаметром всего в 15 см несколько замедляют свой ход. Вращающиеся часы можно рассматривать как близнеца, непрерывно изменяющего свою инерциальную систему отсчета (или как близнеца, на которого воздействует гравитационное поле, если считать диск покоящимся, а космос – вращающимся). Этот опыт является прямой проверкой парадокса близнецов. Наиболее прямой опыт будет выполнен тогда, когда ядерные часы поместят на искусственном спутнике, который будет вращаться с большой скоростью вокруг Земли.

Затем спутник возвратят и показания часов сравнят с теми часами, которые оставались на Земле. Конечно, быстро приближается то время, когда космонавт сможет сделать самую точную проверку, захватив ядерные часы с собой в далекое космическое путешествие. Никто из физиков, кроме профессора Дингля, не сомневается, что показания часов космонавта после его возвращения на Землю будут немного не совпадать с показаниями ядерных часов, оставшихся на Земле.

Из книги
автора

8. Парадокс близнецов
Какова была реакция всемирно известных ученых и философов на странный, новый мир относительности? Она была различной. Большинство физиков и астрономов, смущенные нарушением «здравого смысла» и математическими трудностями общей теории

Специальные и общие теории относительности говорят о том, что у каждого наблюдателя свое время. То есть, грубо говоря, один человек движется и по своим часам определяет одно время, другой человек как-то движется и по своим часам определяет другое время. Безусловно, если эти люди движутся относительно друг друга с небольшими скоростями и ускорениями, они измеряют практически одно и то же время. По нашим часам, которые мы используем, мы это отличие измерить неспособны. Я не исключаю, что если часами, которые измеряют время с точностью до одной секунды за время жизни Вселенной, будут оснащены два человека, то, походив как-то по-разному, они, возможно, увидят какую-то разницу в каком-то n знаке. Однако эти различия слабые.

Специальные и общие теории относительности предсказывают, что эти различия будут существенными, если два товарища друг относительно друга движутся с большими скоростями, ускорениями или вблизи черной дыры. Например, один из них далеко от черной дыры, а другой близко к черной дыре или какому-нибудь сильно гравитирующему телу. Или один покоится, а другой движется с какой-то скоростью относительно него или с большим ускорением. Тогда различия будут существенные. Насколько большие, я не говорю, и это измеряется на эксперименте с высокоточными
атомными часами
. Люди летают на самолете, потом привозят, сравнивают, что показали часы на земле, что показали часы на самолете и не только. Таких экспериментов множество, все они согласуются с форменными предсказаниями общей и специальной теории относительности. В частности, если один наблюдатель покоится, а другой относительно него движется с постоянной скоростью, то пересчет хода часов от одного к другому задается преобразованиями Лоренца, как пример.

В специальной теории относительности на основе этого есть так называемый парадокс близнецов, который описан во многих книгах. Заключается он в следующем. Вот представьте себе, что у вас есть два близнеца: Ваня и Вася. Скажем, Ваня остался на Земле, а Вася полетел на альфу Центавра и вернулся. Теперь говорится, что относительно Вани Вася двигался с постоянной скоростью. У него время двигалось медленнее. Он вернулся, соответственно, он должен быть моложе. С другой стороны, парадокс формулируется так: теперь, наоборот, относительно Васи (движение с постоянной скоростью относительно) Ваня движется с постоянной скоростью, несмотря на то что он находился на Земле, то есть, когда Вася вернется на Землю, по идее, у Вани часы должны показывать меньше времени. Кто же из них младше? Какое-то логическое противоречие. Совершенная чушь эта специальная теория относительности, получается.

Факт номер раз: сразу нужно понять, что преобразованиями Лоренца можно пользоваться, если переходить из одной инерциальной системы отсчета в другую инерциальную систему отсчета. И эта логика, что у одного время движется медленнее за счет того, что он движется с постоянной скоростью, только на основе преобразования Лоренца. А у нас в данном случае один из наблюдателей почти инерциальный – тот, который находится на Земле. Почти инерциальный, то есть эти ускорения, с которыми Земля движется вокруг Солнца, Солнце движется вокруг центра Галактики и так далее, – это все маленькие ускорения, для данной задачи заведомо можно этим пренебречь. А второй должен слетать на альфу Центавра. Он должен разогнаться, затормозиться, потом опять разогнаться, затормозиться – это все неинерциальные движения. Поэтому такой наивный пересчет сразу не работает.

Как же правильно объяснить этот парадокс близнецов? Он на самом деле достаточно просто объясняется. Для того чтобы сравнивать время жизни двух товарищей, они должны встречаться. Они должны сначала встретиться в первый раз, оказаться в одной точке пространства в одно и то же время, сравнить часы: 0 часов 0 минут 1 января 2001 года. Потом разлететься. Один из них будет двигаться одним образом, у него как-то часы будут тикать. Другой будет двигаться другим образом, и у него как-то своим образом будут тикать часы. Потом они снова встретятся, вернутся в одну и ту же точку в пространстве, но уже в другое время по отношению к первоначальному. В одно и то же время окажутся в одной и той же точке по отношению к каким-нибудь дополнительным часам. Важно следующее: теперь они могут сравнить часы. У одного натикало столько-то, у другого натикало столько-то. Как это объясняется?

Представьте эти две точки в пространстве и времени, где они встречались в начальный момент и в конечный момент, в момент отлета на альфу Центавра, в момент прилета с альфы Центавра. Один из них двигался инерциально, будем считать для идеала, то есть он двигался по прямой. Второй из них двигался неинерциально, поэтому он в этом пространстве и времени двигался по какой-то кривой – ускорялся, замедлялся и так далее. Так вот одна из этих кривых обладает свойством экстремальности. Ясно, что среди всех возможных кривых в пространстве и времени прямая является экстремальной, то есть она имеет экстремальную длину. Наивно, кажется, что она должна иметь наименьшую длину, потому что на плоскости среди всех кривых наименьшую длину между двумя точками имеет прямая. В пространстве и времени Минковского у него так устроена метрика, так устроен способ измерения длин, прямая имеет наидлиннейшую длину, как это ни странно звучит. Прямая имеет самую большую длину. Поэтому тот, который двигался инерциально, оставался на Земле, измерит больший промежуток времени, чем тот, который летал на альфу Центавра и вернулся, поэтому он будет старше.

Обычно такие парадоксы придумываются для того, чтобы опровергнуть ту или иную теорию. Придумываются самими же учеными, которые занимаются этой областью науки.

Исходно, когда появляется новая теория, ясное дело, что ее вообще никто не воспринимает, особенно если она противоречит каким-то устоявшимся на тот момент данным. И люди просто сопротивляются, это безусловно, придумывают всякие контраргументы и так далее. Это все проходит тяжелейший процесс. Человек борется за то, чтобы его признали. Это всегда связано с долгими промежутками времени и большой нервотрепкой. Возникают вот такие парадоксы.

Кроме парадокса близнецов есть, например, такой парадокс со стержнем и сараем, так называемое Лоренцево сокращение длин, что если вы стоите и смотрите на стержень, который мимо вас летит с очень высокой скоростью, то он выглядит короче, чем он на самом деле есть в той системе отсчета, в которой он покоится. С этим связан вот такой парадокс. Представьте себе ангар или сквозной сарай, у него две дырки, он какой-то длины, неважно какой. Представьте себе, что на него летит этот стержень, собирается пролететь сквозь него. Сарай в своей системе покоя имеет одну длину, скажем 6 метров. Стержень в своей системе покоя имеет длину 10 метров. Представьте себе, что у них скорость сближения такая, что в системе отсчета сарая стержень сократился до 6 метров. Можно посчитать, какая это скорость, но сейчас неважно, она достаточно близка к скорости света. Стержень сократился до 6 метров. Это значит, что в системе отсчета сарая стрежень в какой-то момент целиком поместится в сарай.

Человек, который стоит в сарае, – вот мимо него летит стержень – в какой-то момент увидит этот стержень, целиком лежащий в сарае. С другой стороны, движение с постоянной скоростью относительное. Соответственно, можно рассматривать, как будто бы стержень покоится, а на него летит сарай. Значит, в системе отсчета стержня сарай сократился, причем сократился он в то же число раз, что и стрежень в системе отсчета сарая. Значит, в системе отсчета стержня сарай сократился до 3,6 метра. Теперь в системе отсчета стержня стержень никак не может поместиться в сарай. В одной системе отсчета он помещается, в другой системе отсчета он не помещается. Чушь какая-то.

Ясное дело, что такая теория не может быть верной, – кажется на первый взгляд. Однако объяснение простое. Когда вы видите стержень и говорите: «Он данной длины», это значит, что к вам поступает сигнал от этого и от этого конца стержня одновременно. То есть, когда я говорю, что стержень поместился в сарай, двигаясь с какой-то скоростью, это значит, что событие совпадения этого конца стержня с этим концом сарая одновременно с событием совпадения этого конца стержня с этим концом сарая. Эти два события одновременны в системе отсчета сарая. Но вы же слышали, наверное, что в теории относительности одновременность относительна. Так вот оказывается, что в системе отсчета стержня эти два события неодновременны. Просто сначала совпадает правый конец стержня с правым концом сарая, потом совпадает левый конец стержня с левым концом сарая через какой-то промежуток времени. Этот промежуток времени как раз равен тому времени, за которое эти 10 метров минус 3,6 метра с этой данной скоростью пролетят конец стержня.

Чаще всего теорию относительности опровергают по той причине, что для нее очень легко придумываются подобные парадоксы. Этих парадоксов существует масса. Есть такая книжка Тейлора и Уилера «Физика пространства-времени», она написана достаточно доступным языком для школьников, где подавляющее большинство этих парадоксов разбираются и объясняются с использованием достаточно простых аргументов и формул, как объясняется тот или иной парадокс в рамках теории относительности.

Можно придумать какой-нибудь способ объяснения каждого данного факта, который выглядит проще, чем тот способ, который предоставляет теория относительности. Однако важным свойством специальной теории относительности является то, что она объясняет не каждый отдельный факт, а всю эту совокупность фактов, вместе взятых. Вот если вы придумали объяснение какого-то одного факта, выделенного из всей этой совокупности, пусть оно объясняет этот факт лучше, чем специальная теория относительности, на ваш взгляд, однако еще нужно проверить, что он и все остальные факты тоже объясняет. А как правило, все эти объяснения, которые звучат более просто, не объясняют всего остального. И надо помнить, что в тот момент, когда придумывается та или иная теория, – это действительно какой-то психологический, научный подвиг. Потому что фактов на этот момент существует один, два или три. И вот человек, основываясь на этом одном или трех наблюдениях, формулирует свою теорию.

В тот момент кажется, что она противоречит всему, что было до того известно, если теория кардинальная. Придумываются вот такие парадоксы, чтобы ее опровергнуть, и так далее. Но, как правило, эти парадоксы объясняются, появляются какие-то новые дополнительные экспериментальные данные, они проверяются, соответствуют ли они этой теории. Также из теории следуют какие-то предсказания. Она же основывается на каких-то фактах, что-то там утверждает, из этого утверждения можно что-то вывести, получить и потом сказать, что если эта теория верна, то должно быть так-то и так-то. Идем, проверяем, так это или не так. Так-то. Значит, теория хороша. И так до бесконечности. В общем-то требуется бесконечно много экспериментов, чтобы подтвердить теорию, но на
данный момент
в той области, в которой специальная и
общая теория
относительности применимы, фактов, опровергающих эти теории, не существует.

Мнимые парадоксы СТО. Парадокс близнецов

Путенихин П.В.

[email protected]

В литературе и в интернете до сих пор идут многочисленные дискуссии по этому парадоксу. Предложено и продолжает предлагаться множество его решений (объяснений), из которых делаются выводы как о непогрешимости СТО, так и её ложности. Впервые тезис, послуживший основой для формулировки парадокса, был изложен Эйнштейном в его основополагающей работе по специальной (частной) теор
ии относительности «К электродинамике движущихся тел» в 1905 году:

«Если в точке А находятся двое синхронно идущих часов и мы перемещаем одни из них по замкнутой кривой с постоянной скоростью до тех пор, пока они не вернутся в А (…), то эти часы по прибытии в А будут отставать по сравнению с часами, остававшимися неподвижными…».

В дальнейшем этот тезис получил собственные имена «парадокс часов», «парадокс Ланжевена» и «парадокс близнецов». Последнее название прижилось, и в настоящее время чаще встречается формулировка не с часами, а с близнецами и космическими полётами: если один из близнецов улетает на космическом корабле к звёздам, то по возвращению он оказывается моложе своего остававшегося на Земле брата.

Гораздо реже обсуждается другой, сформулированный Эйнштейном в этой же работе и следующий сразу же за первым, тезис об отставании часов на экваторе от часов, находящихся на полюсе Земли. Смыслы обоих тезисов совпадают:

«… часы с балансиром, находящиеся на земном экваторе, должны идти несколько медленнее, чем точно такие же часы, помещённые на полюсе, но в остальном поставленные в одинаковые условия».

На первый взгляд это утверждение может показаться странным, ведь расстояние между часами неизменно и нет относительной скорости между ними. Но на самом деле на изменение темпа хода часов влияет мгновенная скорость, которая, хотя и меняет непрерывно своё направление (тангенциальная скорость экватора), но все в сумме они дают ожидаемое отставание часов.

Парадокс, кажущееся противоречие в предсказаниях теор
ии относительности возникает, если движущимся близнецом считать того, который оставался на Земле. В этом случае теперь уже улетавший в космос близнец должен ожидать, что остававшийся на Земле брат окажется моложе него. Так же и с часами: с точки зрения часов на экваторе движущимися следует считать часы на полюсе. Таким образом, и возникает противоречие: так кто же из близнецов окажется моложе? Какие из часов покажут время с отставанием?

Чаще всего парадоксу обычно даётся простое объяснение: две рассматриваемые системы отсчета на самом деле не являются равноправными. Близнец, который улетал в космос, в своём полёте не всегда находился в инерциальной системе отсчета, в эти моменты он не может использовать уравнения Лоренца. Так же и с часами.

Отсюда следует сделать вывод: в СТО не может быть корректно сформулирован «парадокс часов», специальная теор
ия не делает двух взаимоисключающих предсказаний. Полное решение задача получила после создания общей теор
ии относительности, которая решила задачу точно и показала, что, действительно, в описанных случаях отстают движущиеся часы: часы улетавшего близнеца и часы на экваторе . «Парадокс близнецов» и часов, таким образом, является рядовой задачей теор
ии относительности.

Задача об отставании часов на экваторе

Мы опираемся на определение понятия «парадокс» в логике как противоречия, полученного в результате логически формально правильного рассуждения, приводящего к взаимно противоречащим заключениям (Энциплопедический словарь), или как два противоположных утверждения, для каждого из которых имеются убедительные аргументы (Логический словарь). С этой позиции, «парадокс близнецов, часов, Ланжевена» парадоксом не является, поскольку нет двух взаимоисключающих предсказаний теор
ии.

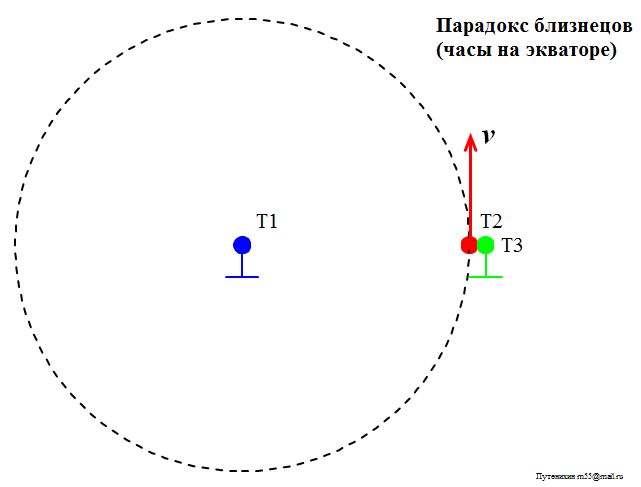
Сначала покажем, что тезис в работе Эйнштейна о часах на экваторе полностью совпадает с тезисом об отставании движущихся часов. На рисунке показаны условно (вид сверху) часы на полюсе Т1 и часы на экваторе Т2. Мы видим, что расстояние между часами неизменно, то есть, между ними, казалось бы, нет необходимой относительной скорости, которую можно подставить в уравнения Лоренца. Однако, добавим третьи часы Т3. Они находятся в ИСО полюса, как и часы Т1, и идут, следовательно, синхронно с ними. Но теперь мы видим, что часы Т2 явно имеют относительную скорость по отношению к часам Т3: сначала часы Т2 находятся на близком расстоянии от часов Т3, затем они удаляются и вновь приближаются. Следовательно, с точки зрения неподвижных часов Т3 движущиеся часы Т2 отстают:

Рис.1 Движущиеся по окружности часы отстают от часов, находящихся в центре окружности. Это становится более очевидно, если добавить неподвижные часы вблизи от траектории движущихся.

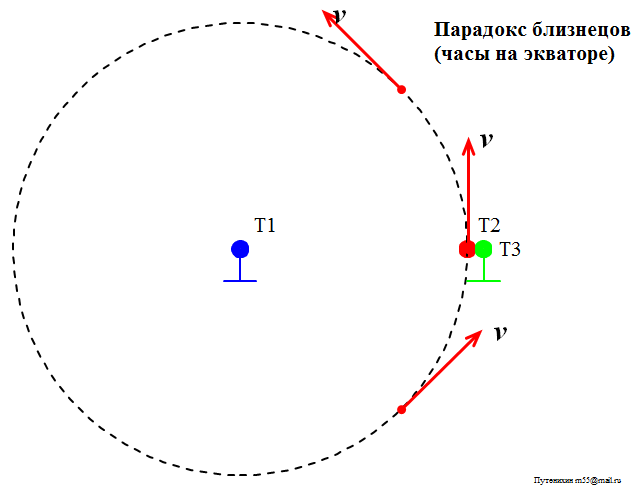
Следовательно, часы Т2 отстают также и от часов Т1. Переместим теперь часы Т3 настолько близко к траектории Т2, что в какой-то начальный момент времени они окажутся рядом. В этом случае мы получаем классический вариант парадокса близнецов. На следующем рисунке мы видим, что сначала часы Т2 и Т3 были в одной точке, затем часы на экваторе Т2 стали удаляться от часов Т3 и по замкнутой кривой через некоторое время вернулись в исходную точку:

Рис.2. Движущиеся по окружности часы Т2 сначала находятся рядом с неподвижными часами Т3, затем удаляются и через некоторое время вновь сближаются с ними.

Это полностью соответствует формулировке первого тезиса об отставании часов, послужившего основой «парадокса близнецов». Но часы Т1 и Т3 идут синхронно, следовательно, часы Т2 отстали также и от часов Т1. Таким образом, оба тезиса из работы Эйнштейна в равной степени могут служить основой для формулировки «парадокса близнецов».

Величина отставания часов в этом случае определяется уравнением Лоренца, в которое мы должны подставить тангенциальную скорость движущихся часов. Действительно, в каждой точке траектории часы Т2 имеют скорости, равные по модулю, но разные по направлениям:

Рис.3 Движущиеся часы имеют постоянно изменяющееся направление скорости.

Как эти разные скорости внести в уравнение? Очень просто. Давайте, в каждую точку траектории часов Т2 поместим свои собственные неподвижные часы. Все эти новые часы идут синхронно с часами Т1 и Т3, поскольку все они находятся в одной и той же неподвижной ИСО. Часы Т2, проходя каждый раз мимо соответствующих часов, испытывает отставание, вызванное относительной скоростью именно мимо этих часов. За мгновенный интервал времени по этим часам, часы Т2 также отстанут на мгновенно малое время, которое можно вычислить по уравнению Лоренца. Здесь и далее мы будем использовать одни и те же обозначения для часов и их показаний:

Очевидно, что верхним пределом интегрирования являются показания часов Т3 в момент, когда часы Т2 и Т3 вновь встретятся. Как видим, показания часов Т2

Как видим, получено решение, полностью совпадающее с решением первого тезиса (с точностью до величин четвертого и высших порядков). По этой причине, дальнейшие рассуждения можно рассматривать как относящиеся ко всем видам формулировок «парадокса близнецов».

Вариации на тему «парадокса близнецов»

Парадокс часов, как отмечено выше, означает, что специальная теор
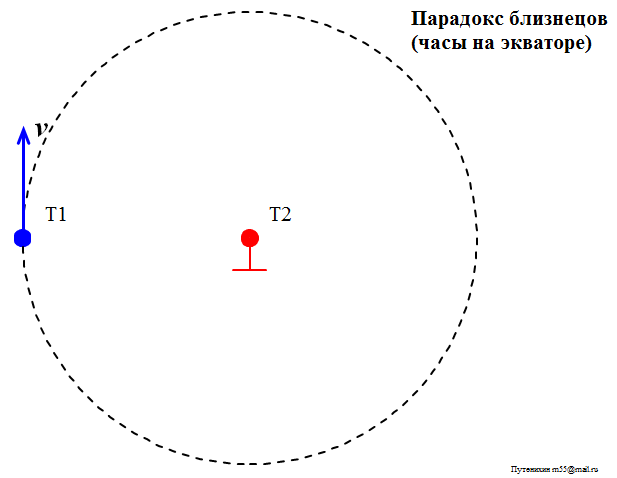
ия относительности, вроде бы, делает два взаимно противоречащих друг другу предсказания. Действительно, как мы только – что вычислили, движущиеся по окружности часы отстают от часов, находящихся в центре окружности. Но и часы Т2, движущиеся по окружности, имеют все основания утверждать, что они находятся в центре окружности, вокруг которой движутся неподвижные часы Т1.

Уравнение траектории движущихся часов Т2 с точки зрения неподвижных Т1:

x, y – координаты движущихся часов Т2 в системе отсчета неподвижных;

R – радиус окружности, описываемой движущимися часами Т2.

Очевидно, что с точки зрения движущихся часов Т2, расстояние между ними и неподвижными часами Т1 также равно R в любой момент времени. Но известно, что геометрическим местом точек, равно удалённых от заданной, является окружность. Следовательно, и в системе отсчета движущихся часов Т2, неподвижные часы Т1 движутся вокруг них по окружности:

x 1 2 + y 1 2 = R 2

x 1 , y 1 – координаты неподвижных часов Т1 в системе отсчета движущихся;

R – радиус окружности, описываемой неподвижными часами Т1.

Рис.4 С точки зрения движущихся часов Т2 вокруг них по окружности движутся неподвижные часы Т1.

А это, в свою очередь, означает, что с точки зрения специальной теор
ии относительности и в этом случае должно возникнуть отставание часов. Очевидно, что в этом случае, наоборот: Т2 > T3 = T. Получается, что и на самом деле специальная теор
ия относительности делает два взаимоисключающих предсказания Т2 > T3 и Т2

Такой опыт рядом с неподвижными часами Т1 даст отрицательный результат, будет наблюдаться невесомость. А вот рядом с движущимися по окружности часами Т2 на все тела будет действовать сила, стремящаяся отбросить их от неподвижных часов. Мы, разумеется, считаем, что никаких иных гравитирующих тел поблизости нет. Кроме того, движущиеся по окружности часы Т2 сами по себе не вращаются, то есть, движутся не так, как Луна вокруг Земли, обращённая к ней всегда одной и той же стороной. Наблюдатели рядом с часами Т1 и Т2 в своих системах отсчета будут видеть удалённый от них на бесконечность объект всегда под одним и тем же углом.

Таким образом, движущийся с часами Т2 наблюдатель должен учесть факт неинерциальности своей системы отсчета в соответствии с положениями общей теор
ии относительности. Эти положения говорят, что часы в поле гравитации или в эквивалентном ему поле инерции, замедляют свой ход. Поэтому в отношении неподвижных (по условиям опыта) часов Т1 он должен признать, что эти часы находятся в гравитационном поле меньшей напряженности, поэтому они идут быстрее его собственных и к их ожидаемым показаниям следует добавить гравитационную поправку.

Напротив, наблюдатель рядом с неподвижными часами Т1 констатирует, что движущиеся часы Т2 находятся в поле инерционной гравитации, поэтому идут медленнее и от их ожидаемых показаний следует отнять гравитационную поправку.

Как видим, мнение обоих наблюдателей полностью совпали в том, что движущиеся в исходном смысл
е часы Т2 отстанут. Следовательно, специальная теор
ия относительности в «расширенной» трактовке делает два строго согласованных предсказания, что не даёт никаких оснований для провозглашения парадоксов. Это рядовая задача, имеющая вполне конкретное решение. Парадокс в СТО возникает лишь в том случае, если использовать её положения к объекту, не являющимся объектом специальной теор
ии относительности. Но, как известно, неверная посылка может привести как к правильному, так и к ложному результату.

Эксперимент, подтверждающий СТО

Следует отметить, что все эти рассмотренные мнимые парадоксы соответствуют мысленным экспериментам на основе математической модели под названием Специальная Теория Относительности. То, что в этой модели данные эксперименты имеют полученные выше решения, не обязательно означает, что в реальном физическом эксперименты будут получены такие же результаты. Математическая модель теор
ии прошла многолетнее испытание и в ней не найдено никаких противоречий. Это значит, что все логически корректные мысленные эксперименты неизбежно будут давать результат, подтверждающий её .

В этой связи представляет особый интерес эксперимент, который общепризнанно в реальных условиях показал точно такой же результат, что и рассмотренный мысленный эксперимент. Непосредственно это означает, что
математическая модель
теор
ии верно отражает, описывает реальные физические процессы.

Это был первый эксперимент по проверке отставания движущихся часов, известный как эксперимент Хафеле – Китинга, проведённый в 1971 г . Четверо часов, сделанных на основе цезиевых стандартов частоты, были помещены на два самолета и совершили кругосветное путешествие. Одни часы путешествовали в восточном направлении, другие обогнули Землю в западном направлении. Разница в скорости хода времени возникала из-за добавочной скорости вращения Земли, при этом учитывалось и влияние поля тяготения на полетной высоте по сравнению с уровнем Земли. В результате эксперимента удалось подтвердить общую теор
ию относительности, измерить различие в скорости хода часов на борту двух самолетов. Полученные результаты были опубликованы в журнале

Scienceв 1972 году.

Литература

1. Путенихин П.В., Три ошибки анти-СТО [прежде, чем критиковать теор
ию, её следует хорошо изучить; невозможно опровергнуть безупречную математику теор
ии её же математическими средствами, кроме как незаметно отказавшись от её постул
атов – но это уже другая теор
ия; не используются известные экспериментальные противоречия в СТО – опыты Маринова и других – их нужно многократно повторить], 2011, URL:

http://samlib.ru/p/putenihin_p_w/antisto.shtml (дата обращения 12.10.2015)

2. Путенихин П.В., Итак, парадокса (близнецов) больше нет! [анимированные диаграммы – решение парадокса близнецов средствами ОТО; решение имеет погрешность вследствие использования приближённого уравнения потенциал
а; ось времени – горизонтальна, расстояний – вертикальна], 2014, URL:

http://samlib.ru/editors/p/putenihin_p_w/ddm4-oto.shtml (дата обращения 12.10.2015)

3. Эксперимент Хафеле-Китинга, Викпиедия, [убедительное подтверждение эффекта СТО о замедлении хода движущихся часов], URL:

https://ru.wikipedia.org/wiki/Эксперимент_Хафеле_—_Китинга (дата обращения 12.10.2015)

4. Путенихин П.В. Мнимые парадоксы СТО. Парадокс близнецов, [парадокс является мнимым, кажущимся, поскольку его формулировка сделана с ошибочными предположениями; корректные предсказания специальной теор
ии относительности не являются противоречивыми], 2015, URL:

http://samlib.ru/p/putenihin_p_w/paradox-twins.shtml (дата обращения 12.10.2015)

Парадокс близнецов

Затем, в 1921 году простое объяснение, основанное на инвариантности собственного времени, предложил Вольфганг Паули .

Некоторое время «парадокс близнецов» почти не привлекал к себе внимания. В 1956-1959 годах Герберт Дингл выступил с рядом статей , в которых утверждалось, что известные объяснения «парадокса» неверны. Несмотря на ошибочность аргументации Дингла , его работы вызвали многочисленные дискуссии в научных и научно-популярных журналах . В результате появился ряд книг, посвящённых этой теме. Из русскоязычных источников стоит отметить книги , а также статью .

Большинство исследователей не считают «парадокс близнецов» демонстрацией противоречия теории относительности, хотя история появления тех или иных объяснений «парадокса» и придания ему новых форм не прекращается до настоящего времени .

Классификация объяснений парадокса

Объяснить парадокс, подобный «парадоксу близнецов», можно при помощи двух подходов:

1) Выявить происхождение логической ошибки в рассуждениях, которые привели к противоречию;
2) Провести детальные вычисления величины эффекта замедления времени с позиции каждого из братьев.

Первый подход зависит от деталей формулировки парадокса. В разделах «

Простейшие объяснения» и «

Физическая причина парадокса» будут приведены различные версии «парадокса» и даны объяснения того, почему противоречия на самом деле не возникает.

В рамках второго подхода расчёты показаний часов каждого из братьев проводятся как с точки зрения домоседа (что обычно не представляет труда), так и с точки зрения путешественника. Так как последний менял свою систему отсчёта , возможны
различные варианты
учёта этого факта. Их условно можно разделить на две большие группы.

К первой группе относятся вычисления на основе специальной теории относительности в рамках инерциальных систем отсчёта. В этом случае этапы ускоренного движения считаются пренебрежимо малыми по сравнению с общим временем полёта. Иногда вводится третья инерциальная система отсчёта, движущаяся навстречу путешественнику, при помощи которой показания его часов «передаются» брату-домоседу. В разделе «

Обмен сигналами» будет приведен простейший расчёт, основанный на эффекте Доплера .

Ко второй группе относятся вычисления, учитывающие детали ускоренного движения . В свою очередь, они делятся по признаку использования или неиспользования в них теории гравитации Эйнштейна (ОТО). Расчёты с использованием ОТО основаны на введении эффективного гравитационного поля , эквивалентного ускорению системы, и учёте изменения в нём темпа хода времени. Во втором способе неинерциальные системы отсчёта описываются в плоском пространстве-времени и понятие гравитационного поля не привлекается. Основные идеи этой группы расчётов будут представлены в разделе «

Неинерциальные системы отсчёта».

Мнение эксперта:

Парадокс близнецов – это гипотетическая ситуация, предложенная Альбертом Эйнштейном, которая иллюстрирует относительность времени в теории относительности. По сценарию парадокса, один из близнецов отправляется в космическое путешествие со скоростью близкой к скорости света, в то время как другой остается на Земле. Из-за различия в скоростях и гравитационных полей, происходит дилатация времени, и по возвращении космонавта обнаруживается, что у него прошло меньше времени, чем у его близнеца на Земле. Этот парадокс демонстрирует, что время относительно и зависит от скорости движения и гравитационного поля, что противоречит нашему ежедневному опыту.

Что такое время? Эксперимент «Парадокс близнецов»

Кинематические эффекты СТО

При этом, чем короче момент ускорения, тем оно больше, и как следствие больше разница в скорости часов на Земле и космического корабля, если он удалён от Земли в момент изменения скорости. Поэтому ускорением никогда нельзя пренебречь.

Конечно, сама по себе констатация несимметричности братьев не объясняет, почему замедлиться должны часы именно у путешественника, а не у домоседа. Кроме этого, часто возникает непонимание:

«Почему нарушение равноправия братьев в течение столь короткого времени (остановка путешественника) приводит к такому разительному нарушению симметрии?»

Чтобы глубже понять причины несимметричности и следствия, к которым они приводят, необходимо ещё раз выделить ключевые посылки, явно или неявно присутствующие в любой формулировке парадокса. Для этого будем считать, что вдоль траектории движения путешественника в «неподвижной» системе отсчёта, связанной с домоседом, расположены синхронно идущие (в этой системе) часы. Тогда возможна следующая цепочка рассуждений, как бы «доказывающих» противоречивость выводов СТО:

1. Путешественник, пролетая мимо любых часов, неподвижных в системе домоседа, наблюдает их замедленный ход.
2. Более медленный темп хода часов означает, что их
   
   накопленныепоказания отстанут от показаний часов путешественника, и при длительном полёте – сколь угодно сильно.
3. Быстро остановившись, путешественник по-прежнему должен наблюдать отставание часов, расположенных в «точке остановки».
4. Все часы в «неподвижной» системе идут синхронно, поэтому отстанут и часы брата на Земле, что противоречит выводу СТО.

Итак, почему путешественник на самом деле будет наблюдать отставание своих часов от часов «неподвижной» системы, несмотря на то, что все такие часы с его точки зрения идут медленнее? Наиболее простым объяснением в рамках СТО является то, что синхронизовать все часы в двух инерциальных системах отсчёта невозможно. Рассмотрим это объяснение подробнее.

Интересные факты

1. Парадокс близнецов – это мысленный эксперимент, который ставит под сомнение наше понимание пространства и времени. Эксперимент был впервые предложен французским математиком Анри Пуанкаре в 1905 году, а затем популяризирован Альбертом Эйнштейном в 1911 году.

2. Парадокс заключается в следующем: если один из близнецов отправляется в путешествие со скоростью, близкой к скорости света, а другой остается на Земле, то по возвращении путешествующего близнеца он окажется моложе своего брата-близнеца. Это происходит потому, что время замедляется для движущихся объектов, и чем быстрее движется объект, тем медленнее для него течет время.

3. Парадокс близнецов является одним из самых известных и обсуждаемых парадоксов в физике. Он ставит под сомнение наше понимание пространства и времени и показывает, что наша интуиция не всегда может быть надежным проводником в мире физики.

Парадокс близнецов. Часть 2 [MinutePhysics]

Физическая причина парадокса

Во время полёта путешественник и домосед находятся в различных точках пространства и не могут сравнивать свои часы непосредственно. Поэтому, как и выше, будем считать, что вдоль траектории движения путешественника в «неподвижной» системе, связанной с домоседом, расставлены одинаковые, синхронно идущие часы, которые может наблюдать путешественник во время полёта. Благодаря процедуре синхронизации в «неподвижной» системе отсчёта введено единое время, определяющее в данный момент «настоящее» этой системы.

После старта путешественник «переходит» в инерциальную систему отсчёта , движущуюся относительно «неподвижной» со скоростью . Этот момент времени принимается братьями за начальный . Каждый из них будет наблюдать замедленный ход часов другого брата.

Однако, единое «настоящее» системы для путешественника перестаёт существовать. В системе отсчёта есть своё «настоящее» (множество синхронизированных часов). Для системы , чем дальше по ходу движения путешественника находятся части системы , тем в более отдалённом «будущем» (с точки зрения «настоящего» системы ) они находятся.

Непосредственно это будущее наблюдать путешественник не может. Это могли бы сделать другие наблюдатели системы , расположенные впереди по движению и имеющие синхронизированное с путешественником время.

Поэтому, хотя все часы в неподвижной системе отсчёта, мимо которых пролетает путешественник, идут с его точки зрения медленнее, из этого

не следует, что они отстанут от его часов.

В момент времени , чем дальше впереди по курсу находятся «неподвижные» часы, тем больше их показания с точки зрения путешественника. Когда он достигает этих часов, они не успеют отстать настолько, чтобы скомпенсировать начальное расхождение времени.

Действительно, положим координату путешественника в преобразованиях Лоренца равной . Закон его движения относительно системы имеет вид . Время, прошедшее после начала полёта, по часам в системе меньше, чем в :

Другими словами, время на часах путешественника отстаёт от показаний часов системы . В то же время часы, мимо которых пролетает путешественник, неподвижны в : . Поэтому их темп хода для путешественника выглядит замедленным:

Таким образом:

несмотря на то, что все конкретные часы в системе идут медленнее с точки зрения наблюдателя в , разные часы

вдоль его траекториибудут показывать время, ушедшее вперед.

Разность темпа хода часов и – эффект относительный, тогда как значения текущих показаний и в одной пространственной точке – носят абсолютный характер. Наблюдатели, находящиеся в различных инерциальных системах отсчёта, но «в одной» пространственной точке, всегда могут сравнить текущие показания своих часов. Путешественник, пролетая мимо часов системы видит, что они ушли вперёд . Поэтому, если путешественник решит остановиться (быстро затормозив), ничего не изменится, и он попадёт в «будущее» системы . Естественно, после остановки темп хода его часов и часов в станет одинаковым. Однако, часы путешественника будут показывать меньшее время чем часы системы , находящиеся в точке остановки. В силу единого времени в системе часы путешественника отстанут от всех часов , в том числе и от часов его брата. После остановки путешественник может вернуться домой. В этом случае весь анализ повторяется. В результате, как в точке остановки и разворота, так и в исходной точке при возвращении путешественник оказывается моложе своего брата-домоседа.

Если же вместо остановки путешественника до его скорости ускорится домосед, то последний «попадёт» в «будущее» системы путешественника. В результате «домосед» окажется моложе «путешественника». Таким образом:

кто изменяет свою систему отсчёта, тот и оказывается моложе.

Опыт других людей

Парадокс близнецов – одно из удивительных явлений, о котором говорят многие. В рамках мысленного эксперимента, предложенного Альбертом Эйнштейном, близнецы отправляются в космос на ракете, один из них летит со скоростью близкой к скорости света. По возвращении близнец, находившийся в космосе, оказывается моложе, чем его брат. Этот феномен объясняется относительностью времени и доказывает, что время искривляется при движении со сверхсветовой скоростью. Парадокс близнецов стал классическим примером для иллюстрации теории относительности и продолжает вдохновлять умы ученых и любознательных людей.

Специальная теория относительности: #8 Парадокс близнецов наглядно. [MinutePhysics]

Обмен сигналами

Вычисление замедления времени с позиции каждого брата можно провести при помощи анализа обмена сигналами между ними. Хотя братья, находясь в различных точках пространства, не могут непосредственно сравнивать показания своих часов, они могут передавать сигналы «точного времени» при помощи световых импульсов или видеотрансляции изображения часов. Понятно, что при этом они наблюдают не «текущее» время на часах брата, а «прошлое», так как сигналу требуется время для распространения от источника к приёмнику.

При обмене сигналами необходимо учитывать эффект Доплера . Если источник удаляется от приёмника, то частота сигнала уменьшается, а когда он приближается – увеличивается:

где – собственная частота излучения, а – частота принимаемого наблюдателем сигнала. Эффект Доплера имеет классическую составляющую и составляющую релятивистскую, непосредственно связанную с замедлением времени. Скорость , входящая в соотношения изменения частоты, является

относительнойскоростью источника и приёмника.

Рассмотрим ситуацию, в которой братья передают друг другу каждую секунду (по своим часам) сигналы точного времени. Проведём сначала расчёт с позиции путешественника.

Расчёт путешественника

Пока путешественник удаляется от Земли, он, в силу эффекта Доплера , регистрирует уменьшение частоты принимаемых сигналов. Видеотрансляция с Земли выглядит более медленной. После быстрого торможения и остановки путешественник перестаёт удаляться от земных сигналов, и их период сразу оказывается равным его секунде. Темп видеотрансляции становится «естественным», хотя, в силу конечности скорости света, путешественник по-прежнему наблюдает «прошлое» своего брата. Развернувшись и разогнавшись, путешественник начинает «набегать» на идущие ему навстречу сигналы и их частота увеличивается. «Движения брата» на видеотрансляции с этого момента начинают выглядеть для путешественника ускоренными .

Время полёта по часам путешественника в одну сторону равно , и такое же в обратную.

Количествопринятых «земных секунд» в течение путешествия равно их частоте , умноженной на время. Поэтому при удалении от Земли путешественник получит существенно меньше «секунд»:

а при приближении, наоборот, больше:

Суммарное количество «секунд», полученных с Земли за время , больше, чем переданных на неё:

в точном соответствии с формулой замедления времени.

Расчёт домоседа

Несколько иная арифметика у домоседа. Пока его брат удаляется, он также регистрирует увеличенный период точного времени, передаваемый путешественником. Однако, в отличие от брата, домосед наблюдает такое замедление

дольше. Время полёта на расстояние в одну сторону составляет по земным часам . Торможение и разворот путешественника домосед увидит спустя дополнительное время , требуемое свету для прохождения расстояния от точки разворота. Поэтому, только через время от начала путешествия домосед зарегистрирует ускоренную работу часов приближающегося брата:

Время движения света от точки разворота выражается через время полёта к ней путешественника следующим образом (см. рисунок):

Поэтому количество «секунд», полученных от путешественника, до момента его разворота (по наблюдениям домоседа) равно:

Сигналы с
повышенной частотой
домосед принимает в течение времени (см. рисунок выше), и получает «секунд» путешественника:

Суммарное число полученных «секунд» за время равно:

Таким образом, соотношение для показания часов в момент встречи путешественника () и брата-домоседа () не зависит от того, с чьей точки зрения оно рассчитывается.

Геометрическая интерпретация

, где – гиперболический арксинус

Рассмотрим гипотетический полёт к звёздной системе Альфа Центавра , удалённой от Земли на расстояние в 4,3 световых года . Если время измеряется в годах, а расстояния в световых годах, то скорость света равна единице, а единичное ускорение св.год/год² близко к ускорению свободного падения и примерно равно 9,5 м/c².

Пусть половину пути космический корабль двигается с единичным ускорением, а вторую половину – с таким же ускорением тормозит (). Затем корабль разворачивается и повторяет этапы разгона и торможения. В этой ситуации время полёта в земной системе отсчёта составит примерно 12 лет, тогда как по часам на корабле пройдёт 7,3 года.
Максимальная скорость
корабля достигнет 0,95 от скорости света.

За 64 года собственного времени космический корабль с единичным ускорением потенциально может совершить путешествие (вернувшись на Землю) к галактике Андромеды , удалённой на 2,5 млн св. лет . На Земле за время такого полёта пройдёт около 5 млн лет. Развивая вдвое большее ускорение (к которому тренированный человек вполне может привыкнуть при соблюдении ряда условий и использования ряда приспособлений, например, анабиоза), можно подумать даже об экспедиции к видимому краю Вселенной (около 14 млрд. св. лет), которая займёт у космонавтов порядка 50 лет; правда, возвратившись из такой экспедиции (через 28 млрд. лет по земным часам), её участники рискуют не застать в живых не то что Землю и Солнце, но даже нашу Галактику. Исходя из этих расчётов, разумный радиус доступности для межзвёздных экспедиций с возвратом не превышает нескольких десятков световых лет, если, конечно, не будут открыты какие-либо принципиально новые физические принципы перемещения в пространстве-времени. Впрочем, обнаружение многочисленных экзопланет даёт основания полагать, что планетные системы встречаются у достаточно большой доли звёзд, поэтому космонавтам будет что исследовать и в этом радиусе (например, планетные системы ε Эридана и Глизе 581).

Расчёт путешественника

Для проведения того же расчёта с позиции путешественника, необходимо задать метрический тензор , соответствующий его неинерциальной системе отсчёта . Относительно этой системы скорость путешественника нулевая, поэтому время на его часах равно

Заметим, что является координатным временем и в системе путешественника отличается от времени системы отсчёта домоседа.

Земные часы свободны, поэтому они движутся вдоль геодезической , определяемой уравнением :

где – символы Кристоффеля , выражающиеся через метрический тензор . При заданном метрическом тензоре неинерциальной системы отсчёта эти уравнения позволяют найти траекторию часов домоседа в системе отсчёта путешественника. Её подстановка в формулу для собственного времени даёт интервал времени, прошедший по «неподвижным» часам:

где – координатная скорость земных часов.

Подобное описание неинерциальных систем отсчёта возможно либо при помощи теории гравитации Эйнштейна , либо без ссылки на последнюю. Детали расчёта в рамках первого способа можно найти, например, в книге Фока или Мёллера . Второй способ рассмотрен в книге Логунова .

Результат всех этих вычислений показывает, что и с точки зрения путешественника его часы отстанут от часов неподвижного наблюдателя. В итоге разница времени путешествия с обеих точек зрения будет одинаковая, и путешественник окажется моложе домоседа. Если длительность этапов ускоренного движения много меньше длительности равномерного полёта, то результат более общих вычислений совпадает с формулой, полученной в рамках инерциальных систем отсчёта.

Выводы

Рассуждения, проводимые в истории с близнецами, приводят только к кажущемуся логическому противоречию. При любой формулировке «парадокса» полной симметричности между братьями нет. Кроме этого, важную роль для понимания того, почему время замедляется именно у путешественника, менявшего свою систему отсчёта, играет относительность одновременности событий.

Расчёт величины замедления времени с позиции каждого брата может быть выполнен как в рамках элементарных вычислений в СТО, так и при помощи анализа неинерциальных систем отсчёта. Все эти вычисления согласуются друг с другом и показывают, что путешественник окажется моложе своего брата-домоседа.

Парадоксом близнецов часто также называют сам вывод теории относительности о том, что один из близнецов состарится сильнее другого. Хотя такая ситуация и необычна, в ней нет внутреннего противоречия. Многочисленные эксперименты по удлинению времени жизни элементарных частиц и замедлению хода макроскопических часов при их движении подтверждают теорию относительности. Это даёт основание утверждать, что замедление времени, описанное в истории с близнецами, произойдёт и при реальном осуществлении этого мысленного эксперимента.

См. также

Примечания

Источники

1. Эйнштейн А. «
   
   К электродинамике движущихся тел», Ann. d. Phys.,1905 b. 17, s. 89, русский перевод в «Эйнштейн А. Собрание
   научных трудов
   в четырёх томах. Том 1. Работы по теории относительности 1905-1920.» М.: Наука, 1965.
2. Langevin P. «
   
   L’evolution de l’espace et du temps». Scientia 10: 31-54. (1911)
3. Laue M. (1913) ”
   
   Das Relativit\”atsprinzip“”. Wissenschaft (No. 38) (2 ed.). (1913)