Чему равна диагональ параллелограмма. Свойство диагоналей параллелограмма. Полные уроки — Гипермаркет знаний

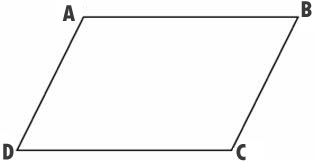
Параллелограмм представляет собой четырехугольник, у которого противоположные стороны попарно параллельны.
Это определение уже достаточно, так как остальные свойства параллелограмма следуют из него и доказываются в виде теорем.

Основными свойствами параллелограмма являются:

• параллелограмм – это выпуклый четырехугольник;
• у параллелограмма противоположные стороны попарно равны;
• у параллелограмма противоположные углы попарно равны;
• диагонали параллелограмма точкой пересечения делятся пополам.

Параллелограмм – выпуклый четырехугольник

Докажем сначала теорему о том, что

параллелограмм является выпуклым четырехугольником. Многоугольник является выпуклым тогда, когда какая бы его сторона не была продлена до прямой, все остальные стороны многоугольника окажутся по одну сторону от этой прямой.

Пусть дан параллелограмм ABCD, у которого AB противоположная сторона для CD, а BC – противоположная для AD. Тогда из определения параллелограмма следует, что AB || CD, BC || AD.

У параллельных отрезков нет общих точек, они не пересекаются. Это значит, что CD лежит по одну сторону от AB. Поскольку отрезок BC соединяет точку B отрезка AB с точкой C отрезка CD, а отрезок AD соединяет другие точки AB и CD, то отрезки BC и AD также лежат по ту же сторону от прямой AB, где лежит CD. Таким образом, все три стороны – CD, BC, AD – лежат по одну сторону от AB.

Аналогично доказывается, что по отношению к другим сторонам параллелограмма три остальные стороны лежат с одной стороны.

Мнение эксперта:

Диагональ параллелограмма равна корню из суммы квадратов его сторон. Это следует из теоремы Пифагора, примененной к треугольнику, образованному диагональю и двумя сторонами параллелограмма. Свойство диагоналей параллелограмма заключается в их равенстве: обе диагонали делятся пополам и пересекаются в точке, которая является их серединой. Полные уроки по этой и другим математическим темам представлены в Гипермаркете знаний, где каждый может найти подробные объяснения и упражнения для углубленного изучения материала.

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия

Противоположные стороны и углы равны

Одним из свойств параллелограмма является то, что

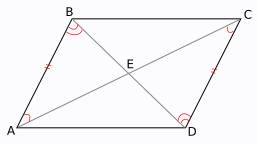
в параллелограмме противоположные стороны и противоположные углы попарно равны. Например, если дан параллелограмм ABCD, то у него AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. Доказывается эта теорема следующим образом.

Параллелограмм является четырехугольником. Значит, у него две диагонали. Так как параллелограмм – это выпуклый четырехугольник, то любая из них делит его на два треугольника. Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC.

У этих треугольников одна сторона общая – AC. Угол BCA равен углу CAD, как вертикальные при параллельных BC и AD. Углы BAC и ACD также равны как вертикальные при параллельных AB и CD. Следовательно, ∆ABC = ∆ADC по двум углам и стороне между ними.

В этих треугольниках стороне AB соответствует сторона CD, а стороне BC соответствует AD. Следовательно, AB = CD и BC = AD.

Углу B соответствует угол D, т. е. ∠B = ∠D. Угол A параллелограмма представляет собой сумму двух углов – ∠BAC и ∠CAD. Угол же C равен состоит из ∠BCA и ∠ACD. Так как пары углов равны друг другу, то ∠A = ∠C.

Таким образом, доказано, что в параллелограмме противоположные стороны и углы равны.

Интересные факты

1. Диагональ параллелограмма делит его на два равных треугольника. Это свойство можно использовать для нахождения площади параллелограмма, так как площадь параллелограмма равна сумме площадей двух треугольников, на которые он делится диагональю.

2. Диагонали параллелограмма пересекаются в точке, которая делит каждую диагональ пополам. Это свойство можно использовать для построения диагоналей параллелограмма, так как достаточно найти точку пересечения диагоналей и провести через нее две прямые, соединяющие противоположные вершины параллелограмма.

3. Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом. Это свойство можно использовать для определения того, является ли параллелограмм ромбом, так как достаточно проверить, перпендикулярны ли его диагонали.

Свойства диагоналей параллелограмма | Геометрия 8-9 классы

Диагонали делятся пополам

Так как параллелограмм – это выпуклый четырехугольник, то у него две две диагонали, и они пересекаются. Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE.

У этих треугольников стороны AB и CD равны как противоположные стороны параллелограмма. Угол ABE равен углу CDE как накрест лежащие при параллельных прямых AB и CD. По этой же причине ∠BAE = ∠DCE. Значит, ∆ABE = ∆CDE по двум углам и стороне между ними.

Также можно заметить, что углы AEB и CED вертикальные, а следовательно, тоже равны друг другу.

Так как треугольники ABE и CDE равны друг другу, то равны и все их соответствующие элементы. Стороне AE первого треугольника соответствует сторона CE второго, значит, AE = CE. Аналогично BE = DE. Каждая пара равных отрезков составляет диагональ параллелограмма. Таким образом доказано, что

диагонали параллелограмма делятся точкой пересечения пополам.

Четырехугольник, противоположные стороны которого параллельны, является параллелограммом. Диагонали — это прямые, соединяющие противоположные вершины. Точка их пересечения является центром симметрии. В общем случае у параллелограмма есть две диагонали, D — длинная и d — короткая.

Опыт других людей

“Чему равна диагональ параллелограмма?” – вопрос, который часто волнует учеников. Однако, благодаря полным урокам по математике в Гипермаркете знаний, это свойство диагоналей параллелограмма становится понятным и доступным. Люди отмечают, что благодаря качественным объяснениям и примерам, они легко усваивают материал и успешно справляются с заданиями.

Сумма квадратов диагоналей параллелограмма

Найти диагональ параллелограмма по теореме косинусов

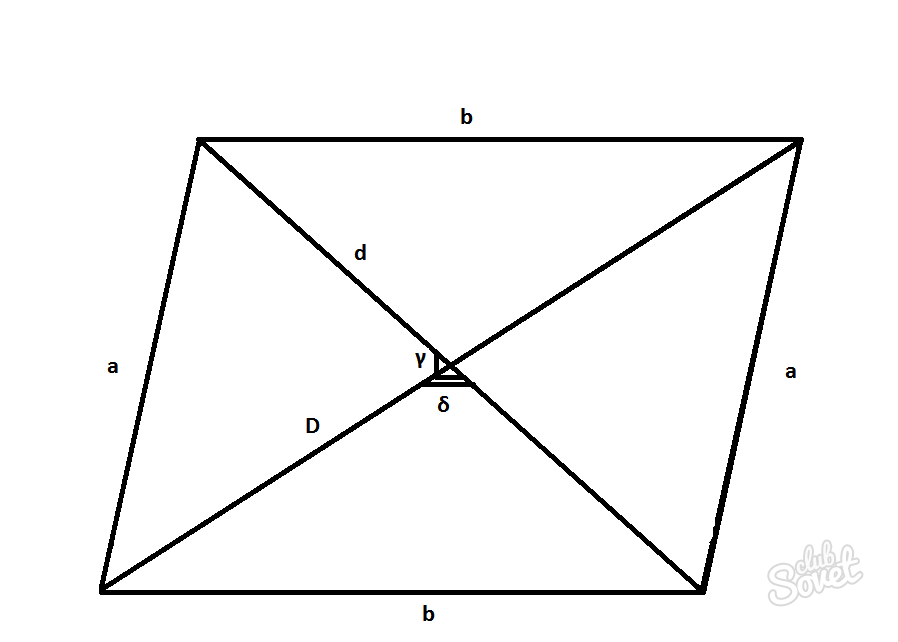
• Значение косинусов углов параллелограмма α и β.

D = √a^2 + b^2 — 2ab·cosβ

d = √a^2 + b^2 + 2ab·cosβ

D = √a^2 + b^2 + 2ab·cosα

d = √a^2 + b^2 — 2ab·cosα

Найти диагональ параллелограмма через одну известную диагональ и стороны

Для применения этого метода необходимо знать:

• Длины сторон параллелограмма a и b.

D = √2a^2 + 2b^2 — d^2

Для применения этого метода необходимо знать:

• Площадь параллелограмма.
• Длину одной из диагоналей D или d.
• Угол между диагоналями γ или δ.

D = 2S/d·sinγ = 2S/d·sinδ

d = 2S/D·sinγ = 2S/D·sinδ

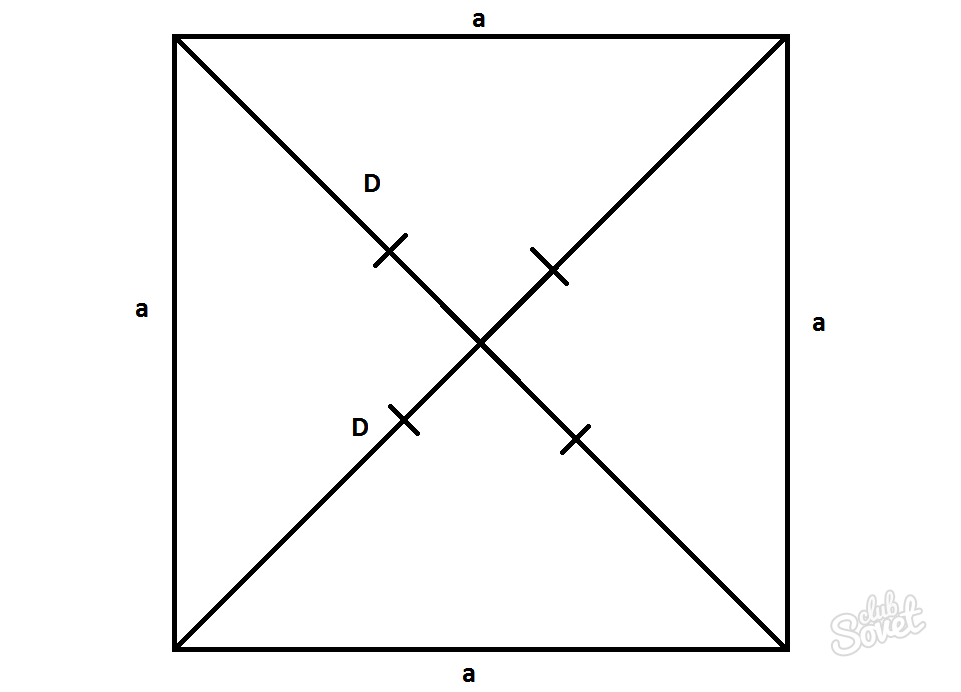
Частный случай определения длины диагонали параллелограмма — квадрат

Квадрат — это параллелограмм, в котором все стороны равны и углы составляют 90°. Длины диагоналей в таком случае будут равны D=d и могут быть рассчитаны по теореме Пифагора.

D=d=a*√2

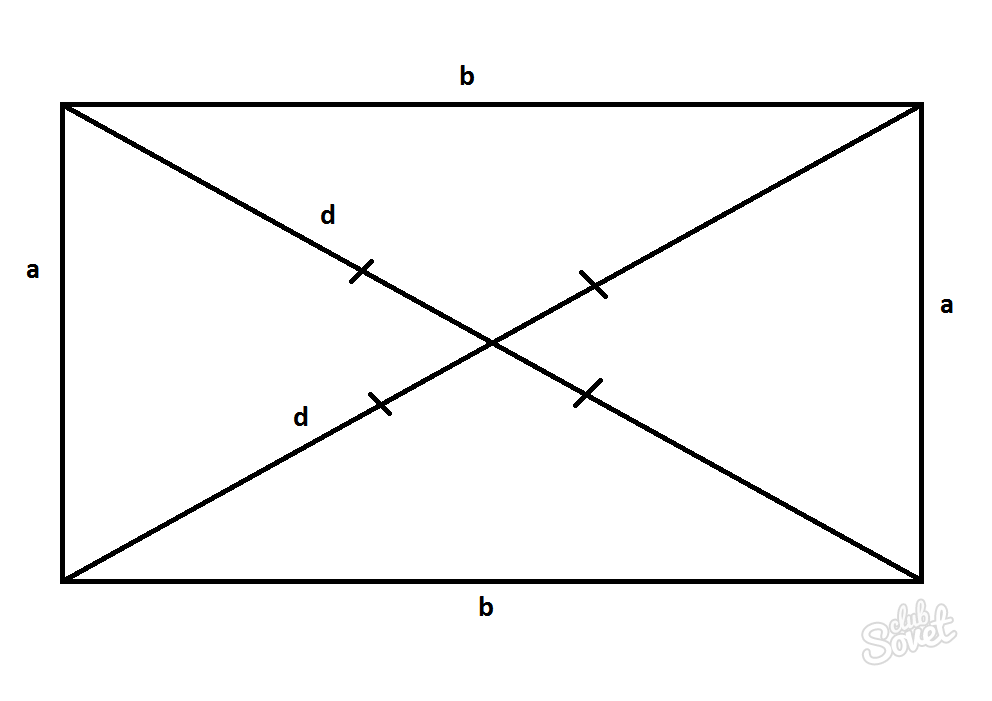
Частный случай определения длины диагонали параллелограмма — прямоугольник

Прямоугольник — это параллелограмм, в котором углы равны и составляют 90°. Длины диагоналей в таком случае будут равны D=d и могут быть рассчитаны по теореме Пифагора.

D=d=√(а^2+b^2)

Свойства параллелограмма.

У параллелограмма противолежащие стороны равны. У параллелограмма противолежащие углы равны.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам (рис. 96).

АВ = CD, ВС = AD, ?BAD = ?BCD, ?АВС = ?ADC, AO = OC, BO = OD.

Признаки параллелограмма.

Если у четырёхугольника две стороны параллельны и равны, то он является параллелограммом (рис. 97).

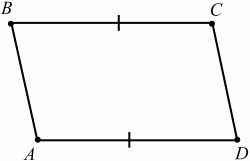
ВС||AD, ВС = AD ? ABCD – параллелограмм.

Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм (рис. 98).

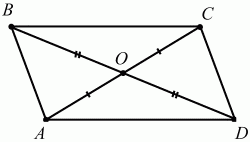
АО = ОС, ВО = OD ? ABCD – параллелограмм.

Свойства прямоугольника.

Для прямоугольника характерны все свойства параллелограмма (у прямоугольника противолежащие стороны равны; у прямоугольника противолежащие углы равны (90°); диагонали прямоугольника пересекаются и точкой пересечения делятся пополам).

Диагонали прямоугольника равны (рис. 99):

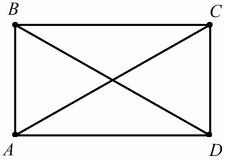
Признак прямоугольника.

Если у параллелограмма все углы равны, то он является прямоугольником.

Свойства ромба.

Для ромба характерны все свойства параллелограмма (у ромба противолежащие стороны равны – вообще все стороны по определению равны; у ромба противолежащие углы равны; диагонали ромба пересекаются и точкой пересечения делятся пополам).

Диагонали ромба пересекаются под прямым углом.

Диагонали ромба являются биссектрисами его углов (рис. 100).

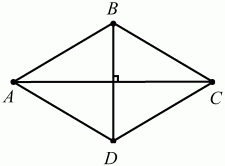
AC ? BD, ?ABD = ?DВС = ?CDB = ?BDA, ?ВАС = ?CAD = ?ВСА = ?DCA.

Признак ромба.

Если у параллелограмма диагонали перпендикулярны, то он является ромбом.

Свойства квадрата.

Квадрат обладает свойствами прямоугольника и ромба.

Признак квадрата.

Если диагонали прямоугольника пересекаются под прямым углом, то он – квадрат.

Свойство
средней линии
трапеции.

Средняя линия трапеции параллельна основаниям и равна их полусумме (рис. 101).

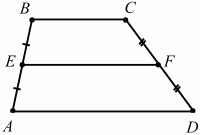
Критерии вписанного и описанного четырехугольников.

Если около четырёхугольника можно описать окружность, то суммы его противоположных углов равны по 180° (рис. 102).

А + ?С = ?В + ?D = 180°.

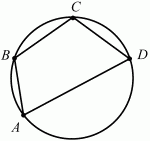
Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны (рис. 103).

AB + CD = AD + BC.

Тема урока

• Свойство диагоналей параллелограмма.

Цели урока

• Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
• Сформулировать и доказать свойство диагоналей параллелограмма.
• Научиться применять свойства фигур при решении задач.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость,
  логическое мышление
  , математическую речь.
• Воспитательные – посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока

• Проверить умение учащихся решать задачи.

План урока

1. Вступительное слово.
2. Повторение ранее изученного материала.
3. Параллелограмм, его свойства и признаки.
4. Примеры задач.
5. Самостоятельная проверка.

Введение

«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия».

Свойство противолежащих сторон параллелограмма

У параллелограмма противолежащие стороны равны.

Доказательство.

Пусть ABCD – данный параллелограмм. И пусть его
диагонали
пересекаются в точке O.

Так как Δ AOB = Δ COD по первому признаку равенства треугольников (∠ AOB = ∠ COD, как вертикальные, AO=OC, DO=OB, по свойству диагоналей параллелограмма), то AB=CD. Точно также из равенства треугольников ВОС и DOA, следует что BC=DA. Теорема доказана.

Свойство противолежащих углов параллелограмма

У параллелограмма противолежащие углы равны.

Доказательство.

Пусть ABCD – данный
параллелограмм
. И пусть его диагонали пересекаются в точке O.

Из доказанного в теореме о свойства противолежащих сторон параллелограмма Δ ABC = Δ CDA по трем сторонам (AB=CD, BC=DA из доказанного, AC – общая). Из равенства треугольников следует, что ∠ ABC = ∠ CDA.

Так же доказывается, что ∠ DAB = ∠ BCD, которое следует из ∠ ABD = ∠ CDB. Теорема доказана.

Свойство диагоналей параллелограмма

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Доказательство.

Пусть ABCD – данный параллелограмм. Проведем диагональ AC. Отметим на ней середину O. На продолжении отрезка DO отложим отрезок OB 1 , равный DO.

По предыдущей теореме AB 1 CD – параллелограмм. Поэтому, прямая AB 1 параллельна DC. Но через точку A можно провести только одну прямую, параллельную DC. Значит, прямая AB 1 совпадает с прямой AB.

Также доказывается, что BC 1 совпадает с BC. Значит, точка С совпадает с С 1 . параллелограмм ABCD совпадает с параллелограммом AB 1 CD. Следовательно, диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Теорема доказана.

В учебниках для обычных школ (например, в Погорелове) доказывается она так: диагонали делят параллелограмм на 4 треугольника. Рассмотрим одну пару и выясним – они равны: основания у них – противоположные стороны, прилежащие к нему соответствующие углы равны как вертикальные при параллельных прямых. То есть отрезки диагоналей попарно равны. Всё.

Всё ли?

Выше доказано, что точка пересечения делит диагонали пополам – если существует. Само её существование приведённое рассуждение не доказывает ни в коей мере. То есть часть теоремы “диагонали параллелограмма пересекаются” остаётся недоказанной.

Забавно, что доказать эту часть намного сложнее. Следует это, кстати, из более общего результата: у любого выпуклого четырёхугольника диагонали будут пересекаться, у любого невыпуклого – не будут.

О равенстве треугольников по стороне и двум прилежащим к ней углам (второй признак равенства треугольников) и другие.

Теореме о равенстве двух треугольников по стороне и двум прилежащим к ней углам Фалес нашел важное практическое применение. В гавани Милета был построен дальномер, определяющий расстояние до корабля в море. Он представлял собой три вбитых колышка А, В и С (АВ = ВС) и размеченную прямую СК, перпендикулярную.СА. При появлении корабля на прямой СК находили точку D такую, чтобы точки D, .В и Е оказывались на одной прямой. Как ясно из чертежа, расстояние CD на земле является искомым расстоянием до корабля.

Вопросы

1. Диагонали квадрата точкой пересечения делятся пополам?
   
2. Диагонали параллелограмма равны?
3. Противолежащие углы параллелограмма равны?
4. Сформулируйте определение параллелограмма?
5. Сколько признаков параллелограмма?
   
6. Может ли ромб быть параллелограмом?
   

Список использованных источников

1. Кузнецов А. В., учитель математики (5-9 класс), г. Киев
2. «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
3. Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
4. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»

Над уроком работали

Кузнецов А. В.

Потурнак С.А.

Евгений Петров

Поставить вопрос о
современном образовании
, выразить идею или решить назревшую проблему Вы можете на

Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав

блог,Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего.

Гильдия Лидеров Образованияоткрывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

Предмети

>

Математика

>

Математика 8 класс

Возможно, будет полезно почитать:

• Пошаговый рецепт морковных оладий: фото и секреты
  ;
• Сколько хранится фаршированный перец в холодильнике
  ;
• Сколько калорий в котлете: диетические рецепты Сколько калорий в мясных и рыбных жареных, запеченных и паровых котлетах
  ;
• Готовим рыбу в нежном молочном соусе
  ;
• Фрикадельки, как сделать фрикадельки из фарша мясного, фрикадельки рыбные
  ;
• Мастер – повар – кулинарная школа
  ;
• Целоваться во сне: к чему такое снится?
  ;
• К чему снится Варить Суп?
  ;

Частые вопросы

Какое существует свойство о диагоналях параллелограмма?

Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам: . Точка пересечения диагоналей является центром симметрии параллелограмма. Параллелограмм диагональю делится на два равных треугольника.

Сколько свойств у параллелограмма?

Свойства параллелограмма: • противоположные стороны попарно равны, • противоположные углы попарно равны, • углы, прилежащие к одной стороне, в сумме дают 180○, • диагонали параллелограмма в точке пересечения делятся пополам.

Как найти площадь параллелограмма через его диагональ?

Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

Как найти стороны параллелограмма если известны диагонали?

a^2 = c^2 — b^2 где a — сторона параллелограмма, b — половина длины одной из диагоналей, c — половина длины другой диагонали.

Полезные советы

СОВЕТ №1

Для вычисления длины диагонали параллелограмма можно воспользоваться теоремой Пифагора, примененной к треугольнику, образованному диагональю и сторонами параллелограмма.

СОВЕТ №2

Из свойства диагоналей параллелограмма следует, что они делятся пополам друг друга. Это означает, что каждая диагональ равна полусумме двух других сторон параллелограмма.