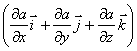СИЛОВОЕ ПОЛЕ— часть пространства (ограниченная или неограниченная),
в каждой точке к-рой на помещённую туда материальную частицу действует
определённая по численной величине и направлению сила, зависящая только
от координат
х, у, zэтой точки. Такое С. п. наз. стационарным;
если сила поля зависит и от времени, то С. п. наз. нестационарным; если
сила во всех точках С. п. имеет одно и то же значение, т. е. не зависит
ни от координат, ни от времени, С. п. наз. однородным.
Стационарное С. п. может быть задано ур-ниями
где
F x , F y , F z— проекции силы
поля F.
Если существует такая ф-ция
U(x, у, z), называемая силовой ф-цией,
что элементарная работа сил поля равна полному дифференциалу этой ф-ции,
то С. п. наз. потенциальным. В этом случае С. п. задаётся одной ф-цией
U(x,
у, z), а сила F может быть определена через эту ф-цию равенствами:
или
. Условие
существования силовой ф-ции для данного С. п. состоит в том, что
или
. При перемещении в потенциальном С. п. из точки
M 1 (x 1 ,
y 1 , z 1)в точку
М 2 (х 2 ,
у 2, z 2) работа сил поля определяется равенством
и не зависит от вида траектории, по к-рои перемещается точка приложения
силы.
Поверхности
U(x, у, z) = const, на к-рых ф-ция сохраняет пост.
значение, наз. поверхностями уровня. Сила в каждой точке поля направлена
по нормали к проходящей через эту точку поверхности уровня; при перемещении
вдоль поверхности уровня работа сил поля равна нулю.
Примеры потенциального С. п.: однородное поле тяжести, для к-рого
U
= -mgz, где
т— масса движущейся в поле частицы,
g— ускорение
силы тяжести (ось
zнаправлена вертикально вверх); ньютоново поле
тяготения, для к-рого
U = km/r, где r =
— расстояние от центра притяжения, k — постоянный для
данного поля
коэффициент.
Вместо силовой ф-ции в качестве характеристики потенциального С. п. можно
ввести
потенциальную энергиюП, связанную с
Uзависимостью
П(х,
у, z)= = —
U(x, у, z). Изучение движения частицы в потенциальном
С. п. (при отсутствии других сил) существенно упрощается, т. к. в этом
случае имеет место закон сохранения механич. энергии, позволяющий установить
прямую зависимость между скоростью частицы и её положением в С. п.
с.
м. Тарг.
СИЛОВЫЕ ЛИНИИ— семейство кривых, характеризующих пространственное
распределение векторного поля сил; направление вектора поля в каждой точке
совпадает с касательной к С. л. Т. о., ур-ния С. л. произвольного векторного
поля
А (х, у, z) записываются в виде:
Плотность С. л. характеризует интенсивность (величину) силового поля.
Область пространства, ограниченная С. л., пересекающими к—л. замкнутую
кривую, наз. силовой трубкой. С. л. вихревого поля замкнуты. С. л. потенциального
поля начинаются на источниках поля и заканчиваются на его стоках (источниках
отрицат. знака).
Понятие С. л. введено М. Фарадеем при исследовании магнетизма, а затем
получило дальнейшее развитие в работах Дж. К. Максвелла по электромагнетизму.
Согласно представлениям Фарадея и Максвелла, в пространстве, пронизываемом
С. л. электрич. и магн. полей, существуют механич. напряжения, соответствующие
натяжению вдоль С. л. и давлению поперёк них. Математически эта концепция
выражена в
Максвелла тензоре натяженийэл—магн. поля.
Наряду с использованием понятия С. л. чаще говорят просто о линиях поля:
напряжённости электрич. поля
Е, индукции магн. поля
Ви т.
п., не делая спец. акцента на отношение этих нолей к силам.
Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке, например поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют
стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.
Работа, которую совершают силы поля при перемещении частицы из точки
1в точку
2, зависит, вообще говоря, от пути. Однако, среди стационарных силовых полей имеются такие, в которых эта работа не зависит от пути между точками
1и
2. Этот класс полей, обладая рядом важнейших свойств, занимает особое место в механике. К изучению этих свойств мы и перейдем.
Поясним сказанное на примере следящей силы. На рис. 5.4 изображено тело
ABCD,в точке
Окоторого приложена сила
,неизменно связанная с телом.
Переместим тело из положения
Iв положение
IIдвумя способами. Выберем вначале в качестве полюса точку
О(рис. 5.4а)) и повернем тело вокруг полюса на угол π/2 противоположно направлению вращения часовой стрелки. Тело займет положение
A»B»C»D».Сообщим теперь телу поступательное перемещение в вертикальном направлении на величину
ОО».Тело займет положение
II (A»B»C»D»).Работа силы на совершенном перемещении тела из положения
Iв положение
IIравна нулю. Вектор перемещения полюса представлен отрезком
ОО».
При втором способе выберем в качестве полюса точку
Kрис. 5.4б) и повернем тело вокруг полюса на угол π/2 против движения часовой стрелки. Тело займет положение
A»B»C»D»(рис. 5.4б). Теперь переместим тело вертикально вверх с вектором перемещения полюса
KK»,после чего дадим телу горизонтальное перемещение влево на величину
K»K».В результате тело займет положение
II,такое же, как на позиции, рис.5.4
а)рисунка 5.4. Однако теперь вектор перемещения полюса будет иным, чем в первом способе, а работа силы при втором способе перемещения тела из положения
Iв положение
IIравна
А = F К»К»,т. е. отлична от нуля.
Определение: стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называют потенциальным, а сами силы –
консервативными.
Потенциаломтаких сил (
потенциальной энергией)называется работа, совершенная ими на перемещениях тела из конечного положения в начальное, причем начальное положение может быть выбрано произвольно. Это означает, что потенциальная энергия определяется с точностью до постоянной.
Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называются
неконсервативными.
В реальных механических системах всегда имеются силы, работа которых при действительном движении системы отрицательна (например, силы трения). Такие силы называются
диссипативными.Они являются частным видом неконсервативных сил.
Консервативные силы обладают рядом замечательных свойств, для выявления которых введем понятие силового поля.
Силовым полем называется пространство(
или его часть)
, в котором на материальную точку, помещенную в каждую точку этого поля, действует некоторая сила.
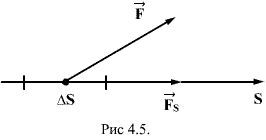
Покажем, что в потенциальном поле работа сил поля на любом замкнутом пути равна нулю. Действительно, любой замкнутый путь (рис. 5.5) можно разбить произвольно на две части,
1а2и
2b1. Так как поле потенциально, то, по условию, . С другой стороны, очевидно, что . Поэтому
что и требовалось доказать.
Обратно, если работа сил поля на любом замкнутом пути равна нулю, то работа этих сил на пути между произвольными точками
1и
2от формы пути не зависит, т. е. поле потенциально. Для доказательства возьмем два произвольных пути
1а2и
1b2(см. рис. 5.5). Составим из них замкнутый путь
1а2b1. Работа на этом замкнутом пути по условию равна нулю, т. е. . Отсюда . Но , поэтому
Таким образом, равенство нулю работы сил поля на любом замкнутом пути есть необходимое и достаточное условие независимости работы от формы пути, и может считаться
отличительным признаком
любого потенциального поля сил.
Поле центральных сил.Всякое силовое поле вызывается действием определенных тел. Сила, действующая на частицу
Ав таком поле, обусловлена взаимодействием этой частицы с данными телами.
Силы, зависящие только от расстояния между взаимодействующими частицами и направленные по прямой, соединяющей эти частицы, называют центральными.Примером последних являются силы гравитационные, кулоновские и упругие.
Центральную силу, действующую на частицу
Асо стороны частицы
В, можно представить в
общем виде
:
где
f(
r) — функция, зависящая при данном характере взаимодействия только от
r— расстояния между частицами; — единичный вектор, задающий направление радиуса-вектора частицы
Аотносительно частицы
В(рис. 5.6).
Докажем, что
всякое стационарное поле центральных сил потенциально.
Для этого рассмотрим сначала работу центральных сил в случае, когда силовое поле вызвано наличием одной неподвижной частицы
В. Элементарная работа силы (5.8) на перемещении есть . Так как — проекция вектора на вектор , или на соответствующий радиус-вектор (рис. 5.6), то . Работа же этой силы по произвольном пути от точки
1до точки
2
Полученное выражение зависит, только от вида функции
f(
r), т. е. от характера взаимодействия, и от значений
r 1и
r 2начального и конечного расстояний между частицами
Аи
В. От формы пути оно никак не зависит. А это значит, что данное силовое поле потенциально.
Обобщим полученный результат на стационарное силовое поле, вызванное наличием совокупности неподвижных частиц, действующих на частицу
Ас силами , каждая из которых является центральной. В этом случае работа результирующей силы при перемещении частицы
Аиз одной точки в другую равна алгебраической сумме работ
отдельных сил
. А так как работа каждой из этих сил не зависит от формы пути, то и работа результирующей силы от нее также не зависит.
Таким образом, действительно, любое стационарное поле центральных сил потенциально.
Потенциальная энергия частицы.То обстоятельство, что работа сил потенциального поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии.
Представим себе, что мы перемещаем частицу в потенциальном поле сил из разных точек
Р iв фиксированную точку
О. Так как работа сил поля не зависит от формы пути, то остается зависимость ее только от положения точки
Р(при фиксированной точке
О). А это значит, что данная работа будет некоторой функцией радиус-вектора точки
Р. Обозначив, эту функцию , запишем
Функцию называют потенциальной энергией частицы в данном поле.
Теперь найдем работу сил поля при перемещении частицы из точки
1в точку
2(рис. 5.7). Так как работа не зависит от пути, возьмем путь проходящий через точку 0. Тогда работа на пути
10
2может быть представлена в виде
или с учетом (5.9)
Выражение, стоящее справа, есть убыль* потенциальной энергии, т. е. разность значений потенциальной энергии частицы в начальной и конечной точках пути.
_________________
* Изменение какой-либо величины
Xможно характеризовать либо ее приращением, либо убылью. Приращением величины
Xназывают разность конечного (
X 2) и начального (
Х 1) значений этой величины:
приращение Δ
Х=
Х 2 — Х 1.
Убылью величины
Xназывают разность ее начального (
Х 1) и конечного (
Х 2) значений:
убыль
Х 1 — Х 2 = —Δ
Х,
т. е. убыль величины
Xравна ее приращению, взятому с обратным знаком.
Приращение и убыль — величины алгебраические: если
Х 2>
X 1, то приращение положительно, а убыль отрицательна, и наоборот.
Таким образом, работа сил поля на пути
1 — 2равна убыли потенциальной энергии частицы.
Очевидно, частице, находящейся в точке 0 поля, всегда можно приписать любое наперед выбранное значение потенциальной энергии. Это соответствует тому обстоятельству, что путем измерения работы может быть определена лишь разность потенциальных энергий в двух точках поля, но не ее абсолютная величина. Однако как только фиксировано значение
потенциальной энергии в какой-либо точке, значения ее во всех остальных точках поля однозначно определяются формулой (5.10).
Формула (5.10) дает возможность найти выражение для любого потенциального поля сил. Для этого достаточно вычислить работу, совершаемую силами поля на любом пути между двумя точками, и представить ее в виде убыли некоторой функции, которая и есть потенциальная энергия .
Именно так и было сделано при вычислении работы в полях упругой и гравитационной (кулоновской) сил, а также в однородном поле тяжести [см. формулы (5.3) — (5.5)]. Из этих формул сразу видно, что потенциальная энергия частицы в данных силовых полях имеет следующий вид:
1) в поле упругой силы
2) в поле точечной массы (заряда)
3) в однородном поле тяжести
Еще раз подчеркнем, что потенциальная энергия
U— это функция, которая определяется с точностью до прибавления некоторой произвольной постоянной. Это обстоятельство, однако, совершенно несущественно, ибо во все формулы входит только разность значений
Uв двух положениях частицы. Поэтому произвольная постоянная, одинаковая для всех точек поля, выпадает. В связи с этим ее обычно опускают, что и сделано в трех предыдущих выражениях.
И еще одно важное обстоятельство, о котором не следует забывать. Потенциальную энергию, строго говоря, следует относить не к частице, а к системе взаимодействующих между собой частицы и тел, вызывающих силовое поле. При данном характере взаимодействия потенциальная энергия взаимодействия частицы с данными телами зависит только от положения частицы относительно этих тел.
Связь между потенциальной энергией и силой. Согласно (5.10), работа силы потенциального поля равна убыли потенциальной энергии частицы, т. е.
А12 =
U1 —
U2 = — (
U2 —
U1). При элементарном перемещении последнее выражение имеет вид
dА= —
dU, или
F l dl= — dU.(5.14)
т. е. проекция силы поля в данной точке на направление перемещения равна с обратным знаком частной производной потенциальной энергии по данному направлению.
, то с помощью формулы (5.16) мы имеем возможность восстановить поле сил .
Геометрическое место точек в пространстве, в которых потенциальная энергия
Uимеет одно и то же значение, определяет эквипотенциальную поверхность. Ясно, что каждому значению
Uсоответствует своя эквипотенциальная поверхность.
Из формулы (5.15) следует, что проекция вектора на любое направление, касательное к эквипотенциальной поверхности в данной точке, равна нулю. Это значит, что вектор нормален к эквипотенциальной поверхности в данной точке. Кроме того, знак минус в (5.15) означает, что вектор направлен в сторону уменьшения потенциальной энергии. Сказанное поясняет рис. 5.8, относящийся к двумерному случаю; здесь изображена система эквипотенциалей, причем
U 1
U 2
U 3
Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из
начального положения
в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю:
К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.
Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.
Силовым полем называется физическое пространство, удовлетворяющее условию, при котором на точки механической системы, находящейся в этом пространстве, действуют силы, зависящие от положения этих точек или от положения точек и времени. Силовое поле. силы которого не зависят от времени, называется стационарным. Стационарное силовое поле называется потенциальным, если существует такая функция, однозначно зависящая от координат точек системы, через которую проекции силы на координатные оси в каждой точке поля выражаются так: X i =∂υ/∂x i ; Y i =∂υ/∂y i ; Z i = ∂υ/∂z i.
Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы , действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии . Следовательно, между силой и потенциальной энергией должна существовать определенная связь.
Для установления этой связи вычислим элементарную работу , совершаемую силами поля при малом перемещении тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой . Эта работа равна
где — проекция силы на направление .
Поскольку в
данном случае
работа совершается за счет запаса потенциальной энергии , она равна убыли потенциальной энергии на отрезке оси :
Из двух последних выражений получаем
Последнее выражение дает среднее значение на отрезке . Чтобы
получить значение в точке нужно произвести предельный переход:
Так как может изменяться не только при перемещении вдоль оси , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от по :
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
в математике вектор
,
где а — скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом . Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком
В пространстве, в каждой точке которого на пробную частицу действует определённая по величине и направлению сила (вектор силы).
Технически различают (как это делается и для других видов полей)
- стационарные поля, величина и направление которых могут зависеть исключительно от точки пространства (координат x, у, z), и
- нестационарные силовые поля, зависящие также от момента времени t.
- однородное силовое поле, для которого сила, действующая на пробную частицу, одинакова во всех точках пространства и
- неоднородное силовое поле, не обладающее таким свойством.
Наиболее простым для исследования является стационарное однородное силовое поле, но оно же представляет собой и наименее общий случай.
Потенциальные поля
Если работа сил поля, действующих на перемещающуюся в нём пробную частицу, не зависит от траектории частицы, и определяется только её начальным и конечным положениями, то такое поле называется потенциальным. Для него можно ввести понятие потенциальной энергии частицы — некоторой функции координат частиц такой, что разность её значений в точках 1 и 2 равна работе, совершаемой полем при перемещении частицы из точки 1 в точку 2.
Сила в потенциальном поле выражается через потенциальную энергию как ее градиент :
Примеры потенциальных силовых полей:
Мнение эксперта:
Силовое поле — это концепция, которая используется в различных областях науки и техники. В физике силовое поле описывает взаимодействие между объектами и силы, действующие на них. В контексте инженерии и техники, силовое поле может относиться к области, в которой материал или устройство обладает особыми свойствами, воздействующими на окружающую среду. В психологии и управлении, силовое поле может означать влияние, которое одна сторона оказывает на другую в рамках взаимодействия или конфликта. Таким образом, понятие силового поля имеет разнообразные интерпретации в зависимости от контекста, в котором оно используется.

Опыт других людей
«Силовое поле» — термин, который часто встречается в разговорах о науке и фантастике. Люди используют его, чтобы описать влияние, мощь или воздействие на окружающее пространство. Некоторые ассоциируют его с энергией, другие — с магией. В общем, «силовое поле» — это концепция, которая вызывает интерес и воображение, и каждый может трактовать ее по-своему.
Интересные факты
-
Силовое поле — это область пространства, в которой на заряженные частицы действует сила. Силовые поля могут быть созданы электрическими зарядами, магнитными полями или гравитацией.
-
Силовые поля используются в различных технологиях, таких как электромоторы, генераторы, ускорители частиц и масс-спектрометры.
-
Силовые поля также играют важную роль в астрофизике. Например, силовые поля, создаваемые магнитными полями звезд, могут удерживать плазму в короне звезды.
![01 [Полярная звезда] Материя: элементарные частицы и силовые поля](https://i.ytimg.com/vi/WCVo__qJ17M/sddefault.jpg)
Литература
Е. П. Разбитная, В. С. Захаров «Курс теоретической физики», книга 1. — Владимир, 1998.
Wikimedia Foundation
.
2010
.
Смотреть что такое «Силовое поле (физика)» в других словарях:
Силовое поле многозначный термин, употребляемый в следующих значениях: Силовое поле (физика) векторное поле сил в физике; Силовое поле (
научная фантастика
) некий невидимый барьер, основная функция которого защита некоторой … Википедия
Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/4 июля 2012. Пока процесс обсуждения не завершён, статью можно по … Википедия
Поле многозначное понятие, связанное с протяжённостью в пространстве: поле в Викисловаре … Википедия
— (от древнегреч. physis природа). Древние называли физикой любое исследование окружающего мира и явлений природы. Такое понимание термина физика сохранилось до конца 17 в. Позднее появился ряд специальных дисциплин: химия, исследующая свойства… …
Энциклопедия Кольера
Силовое поле, действующее на движущиеся
электрические заряды
и на тела, обладающие магнитным моментом (См. Магнитный момент), независимо от состояния их движения. М. п. характеризуется вектором магнитной индукции В, который определяет:… …
Большая советская энциклопедия
СИЛОВОЕ ПОЛЕ
СИЛОВОЕ ПОЛЕ
Часть пространства (ограниченная или неограниченная), в каждой точке к-рой на помещённую туда материальную ч-цу действует , величина и направление к-рой зависят либо только от координат х, у, z этой точки, либо от координат и от времени t. В первом случае С., п. наз. стационарным, а во втором — нестационарным. Если сила во всех точках С. п. имеет одно и то же значение, т. е. не зависит от координат, то С. п. наз. однородным.
С. п., в к-ром сил поля, действующих на перемещающуюся в нём материальную ч-цу, зависит только от начального и конечного положения ч-цы и не зависит от вида её траектории, наз. потенциальным. Эту работу можно выразить через потенциальную энергию ч-цы П (х, у, z):
A=П(x1, y1, z1)-П(x2, y2, z2),
где x1, y1, z1 и х2, y2, z2 — координаты начального и конечного положений частицы соответственно. При движении ч-цы в потенциальном С. п. под действием только сил поля имеет место закон сохранения механич. энергии, позволяющий установить зависимость между скоростью ч-цы и её положением в С. п.
Физический
энциклопедический словарь
. — М.: Советская энциклопедия
.
.
1983
.
СИЛОВОЕ ПОЛЕ
Часть пространства (ограниченная или неограниченная),в каждой точке к-рой на помещённую туда материальную частицу действуетопределённая по численной величине и направлению сила, зависящая толькоот координат
х, у, zэтой точки.
Такое С. п. наз. стационарным;если сила поля зависит и от времени, то С. п. наз. нестационарным; еслисила во всех точках С. п. имеет одно и то же значение, т. е. не зависитни от координат, ни от времени, С. п. наз. однородным.
Стационарное С. п. может быть задано ур-ниями
где
F x , F y , F z —проекции силыполя F.
Если существует такая ф-ция
U(x, у,z), называемая силовой ф-цией, U(x,у, z), а сила F может быть определена через эту ф-цию равенствами:
или
. Условиесуществования силовой ф-ции для данного С. п. состоит в том, что
или . При перемещении в потенциальном С. п. из точки
M 1 (x 1 ,y 1 , z 1)в точку
М 2 (х 2 ,у 2 ,z 2) работа сил поля определяется равенством и не зависит от вида траектории, по к-рои перемещается точка приложениясилы.
Поверхности
U(x, у,z) = const, на к-рых ф-ция сохраняет пост. Примеры потенциального С. п.: однородное поле тяжести, для к-рого
U= -mgz,где
т —масса движущейся в поле частицы,
g —ускорениесилы тяжести (ось
zнаправлена вертикально вверх); ньютоново полетяготения, для к-рого
U = km/r,где r =
— расстояние от центра притяжения, k — постоянный для данного поля коэффициент. потенциальную энергию П, связанную с
Uзависимостью
П(х,)= = —
U(x, у,z). Изучение движения частицы в потенциальномС. п. (при отсутствии других сил) существенно упрощается, т. к. в этомслучае имеет место закон сохранения механич. энергии, позволяющий установитьпрямую зависимость между скоростью частицы и её положением в С. п.
с.
СИЛОВЫЕ ЛИНИИ— семейство кривых, характеризующих пространственноераспределение векторного поля сил; направление вектора поля в каждой точкесовпадает с касательной к С. л. Т. о., ур-ния С. л. произвольного векторногополя
А (х, у,z) записываются в виде:
Плотность С. л. характеризует интенсивность (величину) силового поля. Понятие С. л. введено М. Фарадеем при исследовании магнетизма, а затемполучило дальнейшее развитие в работах Дж. К. Максвелла по электромагнетизму. Максвелла тензоре натяжений эл.-магн. поля.
Наряду с использованием понятия С. л. чаще говорят просто о линиях поля:напряжённости электрич. поля
Е,индукции магн. поля
Ви т.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия
.
Главный редактор
А. М. Прохоров
.
1988
.
Смотреть что такое «СИЛОВОЕ ПОЛЕ» в других словарях:
Силовое поле многозначный термин, употребляемый в следующих значениях: Силовое поле (физика) векторное поле сил в физике; Силовое поле (научная фантастика) некий невидимый барьер, основная функция которого защита некоторой … Википедия
Часть пространства, в каждой точке которого на помещенную туда частицу действует определенная по величине и направлению сила, зависящая от координат этой точки, а иногда и от времени. В первом случае силовое поле называют стационарным, а во… …
Большой Энциклопедический словарь
силовое поле— Область пространства, в которой на помещенную туда материальную точку действует сила, зависящая от координат этой точки в рассматриваемой системе отсчета и от времени. [Сборник рекомендуемых терминов. Выпуск 102.
Теоретическая механика
. Академия… …
Справочник технического переводчика
Часть пространства, в каждой точке которого на помещённую туда частицу действует определённая по величине и направлению сила, зависящая от координат этой точки, а иногда и от времени. В первом случае силовое поле называют стационарным, а во… …
Энциклопедический словарь
силовое поле— jėgų laukas statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorinis laukas, kurio bet kuriame taške esančią dalelę veikia tik nuo taško padėties priklausančios jėgos (nuostovusis jėgų laukas) arba nuo taško padėties ir laiko… …
Penkiakalbis aiškinamasis metrologijos terminų žodynas
силовое поле— jėgų laukas statusas T sritis fizika atitikmenys: angl. force field vok. Kraftfeld, n rus. поле сил, n; силовое поле, n pranc. champ de forces, m … Fizikos terminų žodynas
СИЛОВОЕ ПОЛЕ— В физике, этому термину может быть дано точное определение, в психологии оно используется, как правило, метафорически и обычно относится к любому или ко всем влияниям на поведение. Он обычно используется довольно холистически – силовое поле… …
Толковый словарь
по психологии
Часть пространства (ограниченная или неограниченная), в каждой точке которой на помещенную туда материальную частицу действует определённая по величине и направлению сила, зависящая или только от координат x, у, z этой точки, или же от… …
Большая советская энциклопедия
Часть пространства, в каждой точке к рого на помещённую туда частицу действует определённая по величине и направлению сила, зависящая от координат этой точки, а иногда и от времени. В первом случае С. п. наз. стационарным, а во втором… …
Естествознание. Энциклопедический словарь
силовое поле— Область пространства, в которой на помещённую туда материальную точку действует сила, зависящая от координат этой точки в рассматриваемой системе отсчёта и от времени …
Политехнический терминологический толковый словарь
Возможно, будет полезно почитать:
- Тюменское высшее военно-инженерное командное училище имени маршала инженерных войск А
; - Почему ссср ввязался в гражданскую войну в испании Испанская гражданская война 1936 1939 кратко
; - Савинов, Пётр Иванович: биография Капитан вов савинов п и танкист ас
; - Методы решения неопределенных интегралов
; - Основные проблемы, изучаемые на макроэкономическом уровне
; - Свинья скорпион карьера и финансы
; - Как производится расчет пени по налогам: начисление пени, порядок расчета, пример вычислений
; - Дарение полностью самортизированного объекта ОС
;
Частые вопросы
Что вы понимаете под силовым полем?
Силово́е по́ле в физике — это векторное поле в пространстве, в каждой точке которого на пробную частицу действует определённая по величине и направлению сила (вектор силы).
Какие бывают силовые поля?
Силовое поле ничего не пропускает. … Силовое поле пропускает медленно движущиеся объекты и не пропускает быстрые. … Силовое поле пропускает вещество, но не пропускает излучения или поля.Ещё•2 дек. 2023 г.
Что называется полем в физике?
Область пространства, где проявляют себя физические, достоверно зарегистрированные и точно измеренные силы, называется физическим полем. В рамках современной физики рассматриваются четыре их вида: гравитационное (см. здесь), сильных взаимодействий (см.
Можно ли создать силовое поле?
В настоящее время не существует таких источников энергии, которые могли бы создавать силовые поля с теми функциями, которые присутствуют в художественной литературе. В настоящее время не существует технологии, позволяющей правильно распределять энергию для создания силового поля с функциями, описываемыми фантастикой.

Полезные советы
СОВЕТ №1
Изучите основные понятия физики, такие как сила, вектор, поле, чтобы понять силовое поле более глубоко.
СОВЕТ №2
Посмотрите примеры силовых полей в различных областях, таких как электростатика, магнетизм, гравитация, чтобы увидеть их практическое применение.
СОВЕТ №3
Обратитесь к учебным пособиям и онлайн-курсам по физике, чтобы получить более подробное представление о силовых полях и их математическом описании.