Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
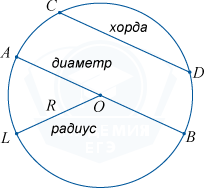
Для любой точки L
, лежащей на окружности, действует равенство OL=R
. (Длина отрезка OL
равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее
хордой.
Хорда, проходящая прямо через центр окружности, является
диаметромэтой окружности (D)
. Диаметр можно вычислить по формуле: D=2R
Длина окружностивычисляется по формуле: C=2\pi R
Площадь круга: S=\pi R^{2}
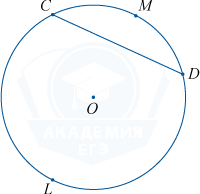
Дугой окружностиназывается та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда CD
стягивает две дуги: CMD
и CLD
. Одинаковые хорды стягивают одинаковые дуги.
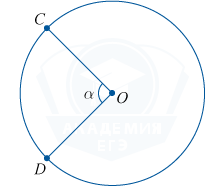
Центральным угломназывается такой угол, который находится между двух радиусов.
Длину дугиможно найти по формуле:
- Используя градусную меру:
CD = \frac{\pi R \alpha ^{\circ}}{180^{\circ}} - Используя радианную меру: CD = \alpha R
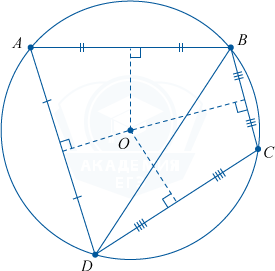
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
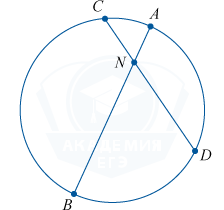
В случае, если хорды AB
и CD
окружности имеют пересечение в точке N
, то произведения отрезков хорд, разделенные точкой N
, равны между собой.
AN\cdot NB = CN \cdot ND
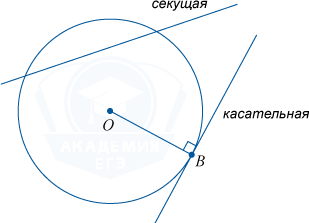
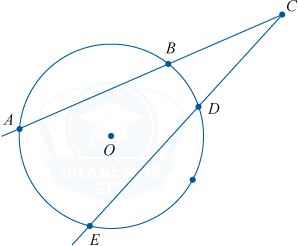
Касательная к окружности
Касательной к окружностипринято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют
секущей.
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
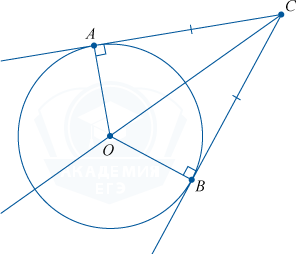
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
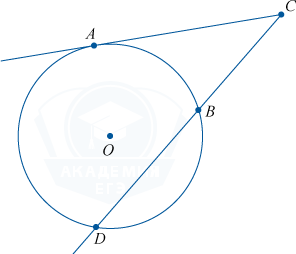
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его
внешнюю часть
.
AC^{2} = CD \cdot BC
Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть.
AC \cdot BC = EC \cdot DC
Мнение эксперта:
Для определения длины окружности по диаметру необходимо воспользоваться формулой C = πd, где C — длина окружности, π — математическая константа, равная примерно 3,14, а d — диаметр окружности. Таким образом, при диаметре 60 мм длина окружности будет равна примерно 188,4 мм.
Также можно использовать формулу C = 2πr, где r — радиус окружности. Если диаметр известен, радиус можно найти, разделив диаметр на 2. После этого можно подставить найденное значение радиуса в формулу для нахождения длины окружности.
Важно помнить, что окружность — это геометрическая фигура, представляющая собой множество точек, равноудаленных от центра. Понимание основных формул и терминологии, связанной с окружностями, позволяет эффективно решать задачи по их изучению и применению в практических ситуациях.

Углы в окружности
Градусные меры центрального угла и дуги, на которую тот опирается, равны.
\angle COD = \cup CD = \alpha ^{\circ}
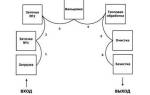
Вписанный угол— это угол, вершина которого находится на окружности, а стороны содержат хорды.
Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги.
\angle AOB = 2 \angle ADB
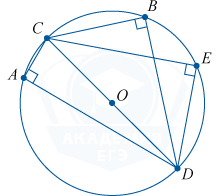
Опирающийся на диаметр, вписанный угол, прямой.
\angle CBD = \angle CED = \angle CAD = 90^ {\circ}
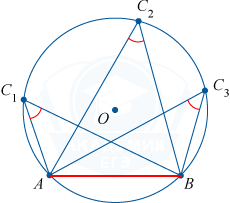
Вписанные углы, которые опираются на одну дугу, тождественны.
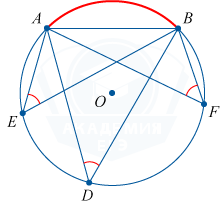
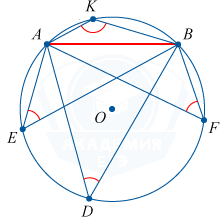
Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется 180^ {\circ}
.
\angle ADB + \angle AKB = 180^ {\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
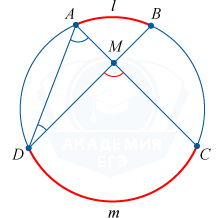
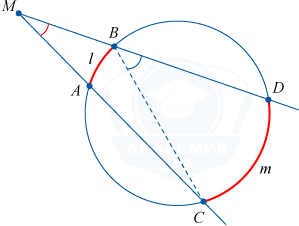
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Интересные факты
Факты:
- Длина окружности равна произведению диаметра на число пи (π).
- Число π — это иррациональное число, которое нельзя представить в виде дроби или десятичной записи с конечным числом знаков после запятой.
- Приближенное значение числа π равно 3,14159265.

Вписанная окружность
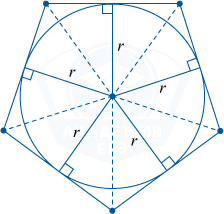
Вписанная окружность— это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr
,
p
— полупериметр многоугольника,
r
— радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
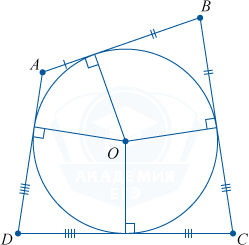
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
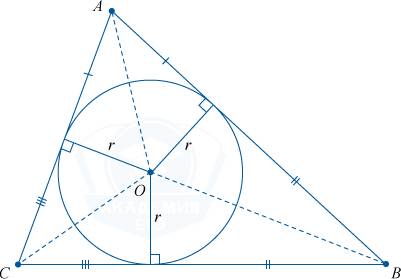
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p}
,
где p = \frac{a + b + c}{2}
Опыт других людей
Если диаметр окружности составляет 60 мм, то для нахождения длины окружности можно воспользоваться формулой \(C = \pi \times d\), где \(C\) — длина окружности, \(\pi\) — математическая константа, примерно равная 3.14, \(d\) — диаметр окружности. Также можно использовать формулу \(C = 2 \times \pi \times r\), где \(r\) — радиус окружности, равный половине диаметра. Эти простые формулы позволяют быстро и точно рассчитать длину окружности. Окружность — это геометрическая фигура, представляющая собой множество точек, равноудаленных от центра. Поэтому знание основных терминов и формул поможет легко решать задачи по геометрии и строительству.

Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть
описанной около многоугольника.
В точке пересечения серединных перпендикуляров сторон этой фигуры будет находиться центр описанной окружности.
Радиус можно найти, вычислив его как радиус окружности, которая описана около треугольника, определенного любыми 3
-мя вершинами многоугольника.
Есть следующее условие: окружность возможно описать около четырехугольника только, если сумма его противоположных углов равна 180^{ \circ}
.
\angle A + \angle C = \angle B + \angle D = 180^ {\circ}
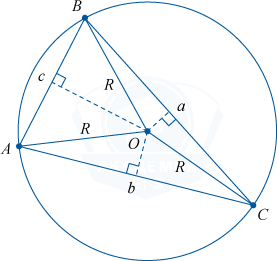
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a
, b
, c
— длины сторон треугольника,
S
— площадь треугольника.
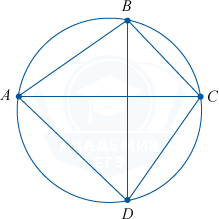
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
В какой бы сфере экономики человек ни трудился, вольно или невольно он пользуется математическими знаниями, накопленными за многие столетия. С устройствами и механизмами, содержащими окружности, мы сталкиваемся ежедневно.
Круглую форму
имеет колесо, пицца, многие овощи и фрукты в разрезе образуют круг, а также тарелки, чашки, да и многое другое. Однако, правильно рассчитывать длину окружности умеет не каждый.
Чтобы вычислить длину окружности, необходимо вначале вспомнить, что такое окружность. Это множество всех точек плоскости, равноудаленных от данной. А круг – это геометрическое место точек плоскости, находящееся внутри окружности. Из вышесказанного следует, что периметр круга и длина окружности – это одно и то же.
Способы нахождения длины окружности
Помимо математического способа нахождения периметра круга, есть и практические.
- Взять веревку или шнур и обернуть один раз вокруг.
- Затем веревку измерить, полученное число и будет длиной окружности.
- Прокатить круглый предмет один раз и посчитать длину пути. Если предмет очень небольшой, можно несколько раз обмотать его бечевкой, затем размотать нить, измерить и поделить на число витков.
- Найти требуемую величину по формуле:
L = 2πr = πD,
где L — искомая длина;
π — константа, приблизительно равна 3,14 r — радиус окружности, расстояние от ее центра до любой точки;
D – диаметр, он равен двум радиусам.
Применение формулы, чтобы найти длину окружности
- Пример 1. Беговая дорожка проходит вокруг окружности радиусом 47,8 метров. Найти длину данной беговой дорожки, приняв π = 3,14.
L = 2πr =2*3,14*47,8 ≈ 300(м)
Ответ: 300 метров
- Пример 2. Колесо велосипеда, обернувшись 10 раз, проехало 18,85 метра. Найти радиус колеса.
18,85: 10 =1,885 (м) — это периметр колеса.
1,885: π = 1,885: 3,1416 ≈ 0,6(м) – искомый диаметр
Ответ: диаметр колеса 0,6 метра
Удивительное число π
Несмотря на кажущуюся простоту формулы, почему-то многим трудно ее запомнить. Видимо, это происходит из-за того, что в формуле есть иррациональное число π, которое не присутствует в формулах площади других фигур, например, квадрата, треугольника или ромба. Нужно просто запомнить, что это константа, то есть постоянная, означающая отношение длины окружности к диаметру. Около 4 тысяч лет назад люди заметили, что отношение периметра круга к его радиусу (или диаметру) одинаково для любых окружностей.
Древние греки приближали число π дробью 22/7. Долгое время π высчитывали как среднее между длинами вписанных и описанных многоугольников в окружность. В третьем столетии нашей эры китайский математик провёл вычисление для 3072-угольника и получил приближённое значение π = 3,1416. Необходимо помнить, что π всегда постоянно для любой окружности. Его обозначение греческой буквой π появилось в 18 веке. Это первая буква греческих слов περιφέρεια — окружность и περίμετρος — периметр. В восемнадцатом веке было доказано, что эта величина иррациональна, то есть ее нельзя представить в виде m/n, где m — целое, а n – натуральное число.
В школьной математике обычно не нужна высокая точность вычислений, и π принимается равным 3,14.
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.
Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой.
Особым случаем
в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу. Формула является достаточно простой и выглядит так: D = C/π = 2*R.
- Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из
разных стран
вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу
повышенной сложности
. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Длина окружности обозначается буквой
Cи вычисляется по формуле:
C = 2πR,
где
R—
радиус окружности.
Вывод формулы, выражающей длину окружности
Путь C и C’ — длины окружностей радиусов R и R’. Впишем в каждую из них правильный n-угольник и обозначим через P n и P» n их периметры, а через a n и a» n их стороны. Используя формулу для вычисления стороны правильного n-угольника a n = 2R sin (180°/n) получаем:
P n = n · a n = n · 2R sin (180°/n),
P» n = n · a» n = n · 2R» sin (180°/n).
Следовательно,
P n / P» n = 2R / 2R». (1)
Это равенство справедливо при любом значении n. Будем теперь неограниченно увеличивать число n. Так как P n → C, P» n → C», n → ∞, то предел отношения P n / P» n равен C / C». С другой стороны, в силу равенства (1) этот предел равен 2R / 2R». Таким образом, C / C» = 2R / 2R». Из этого равенства следует, что C / 2R = C» / 2R», т. е.
отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей.Это число принято обозначать греческой буквой π («пи»).
Из равенства C / 2R = π получаем формулу для вычисления длины окружности радиуса R:
С = 2πR.
Возможно, будет полезно почитать:
- Дело об убийстве царской семьи: что говорят в РПЦ Телеграммы великой драмы
; - Чуть в стороне от царского пути
; - Икона Божьей Матери «Неупиваемая чаша
; - Псориаз: лечение с помощью заговора Церковные православные молитвы от псориаза
; - Преподобный Мефодий Пешношский – основатель Николо-Пешношского монастыря
; - ПП чизкейк: вкусные диетические рецепты Диетический шоколадный чизкейк
; - Вредны ли чипсы Pringles?
; - Подсчитываем калории: в вашей тарелке – печенка говядины
;
Частые вопросы
Как найти размер окружности зная диаметр?
Мы имеем формулу для вычисления длины окружности, если известен диаметр: C = π ⋅ d . Если вспомним, что d = 2 r , то формула длины окружности будет выглядеть так: C = 2 π ⋅ r .
Какой формулой вычисляется длина окружности диаметра D?
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14. Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
Как определить длину окружности по радиусу?
Радиус — это расстояние от центра окружности до ее края. Зная значение радиуса, можно просто умножить его на 2π, чтобы получить длину окружности.
Как найти длину окружности пример?
Длина окружности равна произведению пи π и диаметра d . Так как диаметр d в 2 раз больше радиуса r , длину окружности можно вычислить, зная радиус, по формуле 2πr 2 π r .
Полезные советы
СОВЕТ №1
Запомните основную формулу для расчета длины окружности: L = πd, где L — длина окружности, π — математическая постоянная (приблизительно равная 3,14), d — диаметр окружности.
СОВЕТ №2
Используйте формулу для расчета длины окружности через радиус: L = 2πr, где L — длина окружности, π — математическая постоянная, r — радиус окружности.
СОВЕТ №3
Изучите терминологию, связанную с окружностями, такие как диаметр, радиус, центр окружности, дуга, хорда и т.д., чтобы лучше понимать характеристики этой геометрической фигуры.